C. COUNT TRIANGLES(枚举优化——不等式和的枚举)【不详细你砍我好了5555
http://www.yyycode.cn/index.php/2020/05/18/c-count-triangles%e6%9e%9a%e4%b8%be%e4%bc%98%e5%8c%96-%e4%b8%8d%e7%ad%89%e5%bc%8f%e5%92%8c%e7%9a%84%e6%9e%9a%e4%b8%be/
图片转存失败,不能看的话来我博客
Like any unknown mathematician, Yuri has favourite numbers: AA, BB, CC, and DD, where A≤B≤C≤DA≤B≤C≤D. Yuri also likes triangles and once he thought: how many non-degenerate triangles with integer sides xx, yy, and zz exist, such that A≤x≤B≤y≤C≤z≤DA≤x≤B≤y≤C≤z≤D holds?
Yuri is preparing problems for a new contest now, so he is very busy. That’s why he asked you to calculate the number of triangles with described property.
The triangle is called non-degenerate if and only if its vertices are not collinear.Input
The first line contains four integers: AA, BB, CC and DD (1≤A≤B≤C≤D≤5⋅1051≤A≤B≤C≤D≤5⋅105) — Yuri’s favourite numbers.Output
Print the number of non-degenerate triangles with integer sides xx, yy, and zz such that the inequality A≤x≤B≤y≤C≤z≤DA≤x≤B≤y≤C≤z≤D holds.ExamplesinputCopy
1 2 3 4
outputCopy
4
inputCopy
1 2 2 5
outputCopy
3
inputCopy
500000 500000 500000 500000
outputCopy
1
Note
In the first example Yuri can make up triangles with sides (1,3,3)(1,3,3), (2,2,3)(2,2,3), (2,3,3)(2,3,3) and (2,3,4)(2,3,4).
In the second example Yuri can make up triangles with sides (1,2,2)(1,2,2), (2,2,2)(2,2,2) and (2,2,3)(2,2,3).
In the third example Yuri can make up only one equilateral triangle with sides equal to 5⋅1055⋅105.
题意:给 A<=x<=B<=y<=C<=z<=D,求里面能有多少个三角形
思路:暴力的话x,y,z三个枚举是超时的O(n^3)
稍微优化一点点的枚举x,y,找z然后算D-z也还是超时的。O(n^2)
之后就出了这个优化
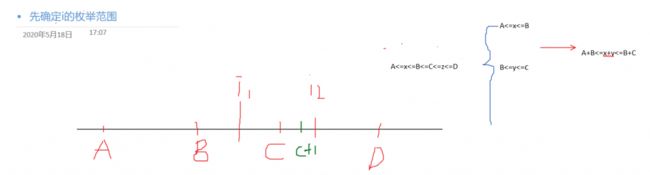
- 先确定i的枚举范围
如果枚举的i(即x+y)在B~C之间,那么肯定不会求出题目要求的z(z>=C)
那么我们要枚举的i实际最少是要C+1 ( 因为如果i==C,是不满足两边之和大于大三边的条件的)
所以for(LL i=max(A+B,C+1);i<=B+C;i++)
- 然后我们来看枚举的i和C-D中间能有多少交集得到这个z
如果i1在C-D之间,那么满足的z的个数是 i1-C
如果i3在D之外,那么整条区间都满足即 D-C+1
那么知道了(x+y)对应的满足的z有多少个,那么我们来找有多少种情况的x,y会构成这样的x+y.
要知道(x+y)这个值是由x,y决定的,也就是说 t=(x+y),然后我们讨论其中一个x或者y
那我们想知道有多少个这样的x+y,只要知道这样的i=x+y有多少个y,或者知道有多少个x就行了。
讨论:y能加的值的最少是多少 (注意枚举过程中 i= x+y是定值),那么问题变成求x能加的最多的是多少,从题目的不等A<=x<=B<=y<=C<=z<=D发现,x最多为B,那么也就是说y=i-B的时候,y是最少的,同时要想到:y=i-B而y的范围要>=B,因此取ymin=max(i-B,B);
同理讨论y能加的值最多为多少,转化到x=i-y的求x的最小,x最小为A,那么i-A是y的最大,同时y<=C,所以取ymax=min(i-A,C);
#include
#include
#include
#include
#include
using namespace std;
const int maxn=1e5;
typedef long long LL;
int main(void)
{
LL A,B,C,D;cin>>A>>B>>C>>D;
LL res=0;
for(LL i=max(C+1,A+B);i<=(B+C);i++)
{
LL ymin=max(i-B,B);
LL ymax=min(i-A,C);
res+=(ymax-ymin+1)*min(i-C,D-C+1);
}
cout<