【数据结构-陪读笔记】第六章:查找
一、线性查找
1.顺序查找
原理: 注意第一个位置上有值;从后面往前面找。
哨兵问题: 避免每次查找位置是否越界。
ASL: n - i + 1求和。
int Search(int a[] , int n , int key){ // n代表数据长度//
int i = n;
a[0] = key;
while(a[i] != key){
i --;
}
return i;
}
2.折半查找
原理: 注意判定树问题。
ASL:
成功:所有圆的就是成功的,所以计算每层圆的个数 * 层数 / 圆的个数
失败:所有方的就是失败的,方的层数 * 层的方的个数 / 方的个数
int Binary_Search(SqList L, ElemType key , int n){
int low = 0 , high = n - 1 , mid; // 从0开始
while(low <= high){
mid = (low + high) / 2; // 向下取整
if(L.elem[mid] == key){ // 正好查到
return mid;
}
else if(L.elem[mid] > key){ // 比它大,右缩小范围
high = mid - 1;
}
else{
low = mid + 1; // 比它小, 左缩小范围
}
}
return -1;
}
3.平衡二叉树
Q:什么是平衡二叉树?
平衡二叉树的左子树-右子树的深度不超过1。
struct node{
int data , height;
node* lchild , rchild;
}
//求出结点的高度
int get_Height(node* root){
if(root == NULL) return 0;
else root->height;
}
//计算平衡因子
int get_BalanceFactor(node* root){
return get_Height(root->lchild) - get_Height(root->rchild);
}
Q:为什么平衡二叉树的ASL与logn为同样的数量级?
根据前面树的四个公式已知(公式链接),n个结点的二叉树的深度为logn向下取整+1,在树中查找一个数据,最多不会超过树的深度吧,所以平均查找长度也就和logn为同样的一个数量级。
Q:如何构建平衡二叉树?
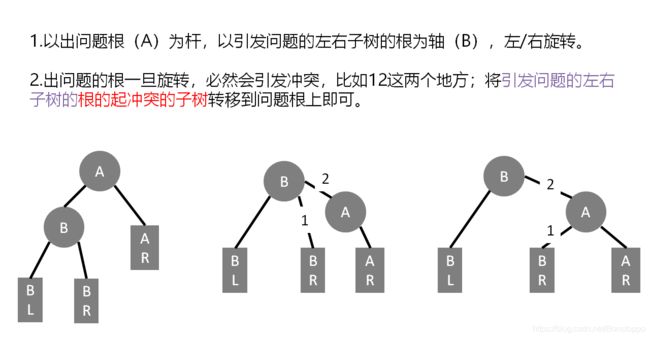
如果是那种RL的那种,记得从下往上依次更新即可。
//Right Rotation
void Right_Rotation(node* &root){
node * temp = root->lchild; // temp当前指向的是B,root是A
root->lchild = temp->rchild; // 让B结点的右孩子成为A结点的左孩子
temp->rchild = root; // 让A结点成为B结点的右孩子
update_Height(root); //分别更新AB结点的高度
update_Height(temp);
root = temp; //根节点变化
}
//更新高度函数,其左右孩子的高度的最大值+1
void update_Height(node* root){
root->height = max(get_Height(root->lchild) , get_Height(root->rchild) + 1);
}
4.B 树
文件系统搜索常用的一种数据结构。
特性
- 每个结点最多有m棵子树。
- 根节点如果是非叶子结点,则至少有2棵子树。(一分为二嘛)
- 除了根节点之外的任何的结点至少有向上取整【m/2】棵子树。
查找分析
B树的查找方式类似二叉排序树,关键字可以理解为就是一种分割点。
- 查找结点。
- 查找结点上的关键字。
对于第二种查找方式,关键问题还是结点的深度。第一层有1个结点,第二层按照定义有2个结点;再往下,由于非叶子结点的子树的个数是 ⌈m/2⌉ ,所以下一层的结点的个数是 2 ∗ ( ⌈ m / 2 ⌉ ) 2*( ⌈m/2⌉) 2∗(⌈m/2⌉);再往下,结点数需要再乘 ⌈m/2⌉,得到 2 ∗ ( ⌈ m / 2 ⌉ ) 2 2*( ⌈m/2⌉)^{2} 2∗(⌈m/2⌉)2次,所以按照这个规律往下递推,第l层有 2 ∗ ( ⌈ m / 2 ⌉ ) l − 2 2*( ⌈m/2⌉)^{l-2} 2∗(⌈m/2⌉)l−2次,第l+1层为叶子结点,有 2 ∗ ( ⌈ m / 2 ⌉ ) l − 1 2*( ⌈m/2⌉)^{l-1} 2∗(⌈m/2⌉)l−1次。
当前B树有 N N N个关键字,如果查找不成功,则结点个数为 N + 1 N+1 N+1个,(我的理解是,当前的关键字的个数和结点个数的值是一致的。)这个数值肯定比当前结点数值要小嘛,所以可以得到
N + 1 ≤ 2 ∗ ⌈ m / 2 ⌉ l − 1 N+1\leq{2*\lceil m/2 \rceil}^{l-1} N+1≤2∗⌈m/2⌉l−1
推导可以得到一个关于 l l l的公式,即
l ≤ l o g ⌈ m / 2 ⌉ ( N + 1 2 ) + 1 l\leq log_{\lceil m/2 \rceil}(\frac{N+1}{2})+1 l≤log⌈m/2⌉(2N+1)+1
插入分析
Q1:何时产生分裂?为什么说该结点关键字个数不超过 m − 1 m-1 m−1时不需要分裂?
根据树的定义,树的每个结点不能有超过m棵子树,m棵子树对应的根会有 m − 1 m-1 m−1个关键字。(可以想想5个手指算上左右的空隙会有6个空隙。)
Q2:怎么插?
- 0 0 0到 ⌈ m / 2 ⌉ − 1 \lceil m/2 \rceil-1 ⌈m/2⌉−1这部分成为左子树; ⌈ m / 2 ⌉ \lceil m/2\rceil ⌈m/2⌉往上回到根节点上,其余放到右节点上;如果是根节点就让中间的结点不动,其余的结点往下放即可。
- 先根据树找到结点先插进去,随后再对树进行调整。
删除分析
删除的本质其实在于:如何在维持B树的定义的情况下删除一个关键字。
如果删除的是非终端叶子结点,将该结点子树的最小的叶子结点进行交换即可。所以书上写着有三种情况。
根据树的定义:除根以外的所有的结点都是 ⌈ m / 2 ⌉ \lceil m/2 \rceil ⌈m/2⌉当差了一个1,正好可以维持。所以当缺少了一个数值的时候,可以从左右借。
- 能删则删: 若删除结点关键字个数不小于 ⌈ m / 2 ⌉ \lceil m/2 \rceil ⌈m/2⌉,则直接删除。
- 能借则借: 若删除结点A的关键字数目等于 ⌈ m / 2 ⌉ − 1 \lceil m/2 \rceil-1 ⌈m/2⌉−1,且兄弟结点 B B B关键字数目大于 ⌈ m / 2 ⌉ − 1 \lceil m/2 \rceil-1 ⌈m/2⌉−1,设其双亲结点为 C C C,则从 C C C中下放 A A A一个数据,从 B B B中上交一个数据补充给 C C C。
- 不能合并: 若AB关键字数目都等于 ⌈ m / 2 ⌉ − 1 \lceil m/2 \rceil-1 ⌈m/2⌉−1,则直接从C下放一个数据给A,然后AB合并。如果导致父结点数据不够了,则依次往上进行调整。
5.B+ 树
B+树的数据都存在在叶子结点上,然后用一个链表把所有的叶子结点都串了起来。当数据存储的离根节点很近的时候,B树效果比B+树效果要好,B+数据都存在叶子结点上。
二、计算查找–Hash表
查找分为两种,一种是上面介绍的通过比较的查找,而另一种则是根据计算直接得出。关键字 k e y key key 和其对应的hash函数的 h a s h ( k e y ) hash(key) hash(key)合成一个表,成为hash表或者散列表。
hash表非常容易算错,一定要仔细仔细再仔细,算的是余数不是商。
构造方法
- 直接定值法:利用线性函数直接定义,但是发现其实本身并没有起到压缩的作用。
- 数字分析法:选取比较随机的几位进行叠加舍去进位作为hash地址。
- 平方取中法:关键字平方后利用中间的几位数字作为hash地址。
- 折叠法:关键字拆分成几个部分叠加和再合并。
- 随机数:random函数。
- 除留取余法:p选取质数(假设选取合数,余数必然都会是0,没什么意义了)或者不包含小于20的质因数的合数。 H a s h ( k e y ) = k e y % p , p < = M Hash(key)=key \%p, p<= M Hash(key)=key%p,p<=M
处理冲突
- 开放地址法:m代表hash表长,d有3种情况(1)线性探测再散列(线性。当发现起了冲突的时候+1,如果再起冲冲突再+1,相当于出了冲突之后不停的往后一个一个查找)(2)二次探测再散列: + 1 2 , − 1 2 , + 2 2 , − 2 2 . . . m / 2 2 +1^2,-1^2,+2^2,-2^2...{m/2}^2 +12,−12,+22,−22...m/22(3)伪随机数列。
- 再Hash:再给一个Hash函数再计算一次。
- 链地址:类似邻接表。
- 设置公共溢出区:但凡发生了冲突的,都写到公共溢出区。
性能分析
从上面可以看到hash函数的问题主要是出现在hash函数的设计,处理冲突的方法,以及当前hash函数已经存储的状态。所以同样hash查找也可以利用ASL进行分析。
- 关于状态因子的问题: α = 表 中 填 入 的 记 录 数 h a s h 表 长 \alpha=\frac{表中填入的记录数}{hash表长} α=hash表长表中填入的记录数
装填因子本身可以理解为当前hash表的存储的利用率。如果本身 α \alpha α小,代表表中本身没有什么东西,所以发生冲突的可能性就小;反之大。