【算法】网络流之最大流~~
流啊流~流啊流~,流成最大流~
网络流是个是个神奇的玩意~
今天先写一个最大流的博文记录咯。
=======================散发着神秘气息的分割线=======================
FCBayern!
首先要学习网络流,我们要知道一些定义哦。当然这些定义和图的定义是差不多的呢~
V表示整个图中的所有结点的集合.
E表示整个图中所有边的集合.
G = (V,E) ,表示整个图.
s表示网络的源点,t表示网络的汇点.
对于每条边(u,v),有一个容量c(u,v) (c(u,v)>=0)
如果c(u,v)=0,则表示(u,v)不存在在网络中。
如果原网络中不存在边(u,v),则令c(u,v)=0
对于每条边(u,v),有一个流量f(u,v)。
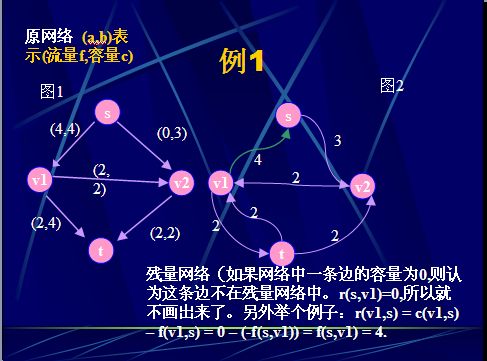
网络流,顾名思意就是要“流”,那么用一个简单的说法就是像水管一样,有水在里面流~,比如这幅图:左边表示里面的水流量,右边表示这个水管的最大流量。
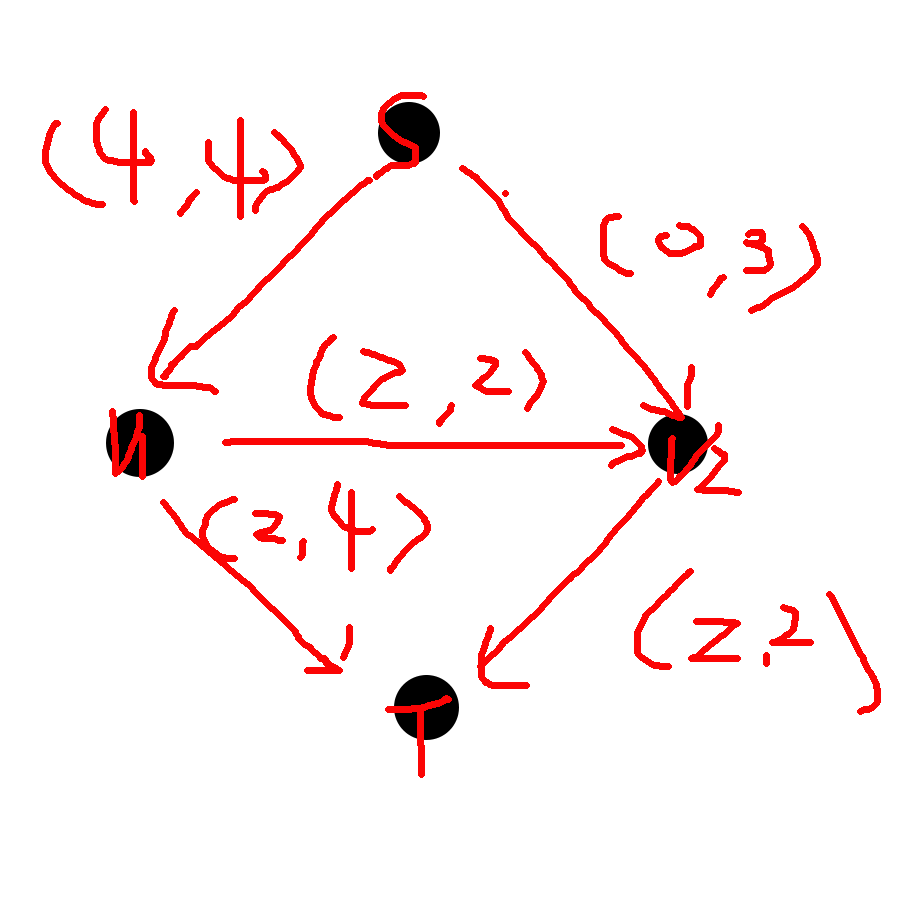
那么网络流的限制是神马捏?
、容量限制: f[u,v]<=c[u,v]
2、反对称性:f[u,v] = - f[v,u]
3、流量平衡: 对于不是源点也不是汇点的任意结点,流入该结点的流量和等于流出该结点的流量和。
结合反对称性,流量平衡也可以写成:
∑u∈Vf(u,v)
只要满足这三个性质,就是一个合法的网络流。
那最大流就是指能流到汇点的最大流量。
定义一个网络的流量(记为|f|)
∑v∈Vf(s,v)
求一个|f|合法的最大值。
当然这里还要引入一个叫残量网络的定义,在最大流算法中会得到运用:
为了更方便算法的实现,一般根据原网络定义一个残量网络。其中r(u,v)为残量网络的容量。
r(u,v)=c(u,v)–f(u,v)
通俗地讲:就是对于某一条边(也称弧),还能再有多少流量经过。
Gf 残量网络, Ef 表示残量网络的边集。
除了残量路径,还有一个东西叫后向弧:
其中像(v1,s)这样的边称为后向弧,它表示从v1到s还可以增加4单位的流量。
那么问题来了:
从v1到s不是和原网络中的弧的方向相反吗?显然“从v1到s还可以增加4单位流量”这条信息毫无意义。那么,有必要建立这些后向弧吗?
答案是肯定的!
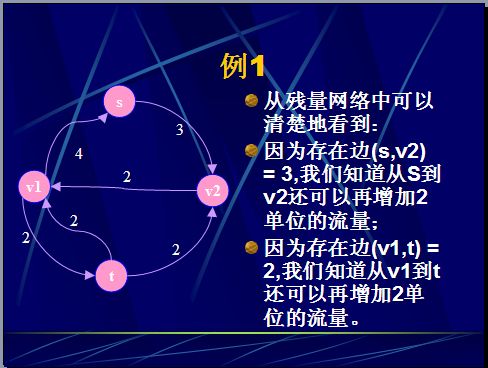
显然,例1中的画出来的不是一个最大流。
但是,如果我们把 s−>v2−>v1−>t 这条路径经过的弧的流量都增加2,就得到了该网络的最大流。
注意到这条路径经过了一条后向弧:(v2,v1)。
如果不设立后向弧,算法就不能发现这条路径。
从本质上说,后向弧为算法纠正自己所犯的错误提供了可能性,它允许算法取消先前的错误的行为(让2单位的流从v1流到v2)。
这样子,我们经过很多次处理后,就可以得到最大流哦~不过事实上后向弧这玩意和普通路径没什么区别,不过是为了处理更简单罢了。
为了实现算法,我们还要知道一个叫做增广路的东西:
增广路定义:在残量网络中的一条从s通往t的路径,其中任意一条弧(u,v),都有r[u,v]>0。
求最大流的方法Ford-Fulkerson
Ford-Fulkerson方法依赖于三种重要思想,这三个思想就是残留网络,增广路径和割。Ford-Fulkerson方法是一种迭代的方法。开始时,对所有的u,v∈V有f(u,v)=0,即初始状态时流的值为0。在每次迭代中,可通过寻找一条“增广路径”来增加流值。增广路径可以看成是从源点s到汇点t之间的一条路径,沿该路径可以压入更多的流,从而增加流的值。反复进行这一过程,直至增广路径都被找出来,根据最大流最小割定理,当不包含增广路径时,f是G中的一个最大流。在算法导论中给出的Ford-Fulkerson实现代码如下
FORD_FULKERSON(G,s,t)
for each edge(u,v)∈E[G]
do f[u,v] <— 0
f[v,u] <— 0
while there exists a path p from s to t in the residual network Gf
do cf(p) <— min{ cf(u,v) : (u,v) is in p }
for each edge(u,v) in p
do f[u,v] <— f[u,v]+cf(p) //对于在增广路径上的正向的边,加上增加的流
f[v,u] <— -f[u,v] //对于反向的边,根据反对称性求第1~3行初始化各条边的流为0,第4~8就是不断在残留网络Gf中寻找增广路径,并沿着增广路径的方向更新流的值,直到找不到增广路径为止。而最后的最大流也就是每次增加的流值cf(p)之和。在实际的实现过程中,我们可以对上述代码做些调整来达到更好的效果。如果我们采用上面的方法,我们就要保存两个数组,一个是每条边的容量数组c,一个就是上面的每条边的流值数组f,在增广路径中判断顶点u到v是否相同时我们必须判断c[u][v]-f[u][v]是否大于0,但是因为在寻找增广路径时是对残留网络进行查找,所以我们可以只保存一个数组c来表示残留网络的每条边的容量就可以了,这样我们在2~3行的初始化时,初始化每条边的残留网络的容量为G的每条边的容量(因为每条边的初始流值为0)。而更新时,改变7~8行的操作,对于在残留网络上的边(u,v)执行 c[u][v]−=cf(p) ,而对其反向的边(v,u)执行 c[v][u]+=cf(p) 即可。
现在剩下的最关键问题就是如何寻找增广路径。而Ford-Fulkerson方法的运行时间也取决于如何确定第4行中的增广路径。如果选择的方法不好,就有可能每次增加的流非常少,而算法运行时间非常长,甚至无法终止。对增广路径的寻找方法的不同形成了求最大流的不同算法,这也是Ford-Fulkerson被称之为“方法”而不是“算法”的原因。
要实现这个方法,就遇到了三个问题:
(1)最多要增广多少次?
可以证明 最多O(VE)次增广 可以达到最大流 证明在这最后吧!
(2)如何找到一条增广路?
先明确什么是增广路: 增广路是这样一条从s到t的路径 路径上每条边残留容量都为正。把残留容量为正的边设为可行的边 那么我们就可以用简单的BFS得到边数最少的增广路。
(3)BFS得到增广路之后 这条增广路能够增广的流值, 是路径上最小残留容量边决定的。
把这个最小残留容量MinCap值加到最大流值Flow上, 同时路径上每条边的残留容量值减去MinCap。
最后,路径上每条边的反向边残留容量值要加上MinCap
接下来介绍两中找增广路的方法:
第一种是Edmonds-Karp(EK),这种做法就是用BFS来找到一条最短的增广路径,仅此而已。
模板:
#includeif(!vis[t])
return false;
return true;
}
void EK(int s,int t)
{
while(bfs(s,t))
{
for(int i=t;i!=s;i=pre[i])
{
flow[pre[i]][i]+=vis[t];
flow[i][pre[i]]-=vis[t];
}
ans+=vis[t];
}
}
int main()
{
// freopen("1.in","r",stdin);
while(~scanf("%d%d",&n,&m))
{
ans=0;
memset(cap,0,sizeof(cap));
memset(flow,0,sizeof(flow));
for(int i=0;iscanf("%d%d%d",&u,&v,&w);
cap[u][v]+=w;
}
EK(1,m);
printf("%d\n",ans);
}
} 其中,cap表示可流流量,而flow表示当前流量,vis[t]表示最小残留容量。
这种方法显然易懂,就不多说了,和普通bfs是差不多了。
第二种是Dinic算法。
这种算法号称是时间复杂度最优的算法,它的主旨在于把多次找增广路的过程简化,构造成类似一座楼,一层一层的层次图。
建立一个辅助网络L,L与原网络G具有相同的节点数,但边上的容量有所不同,在L上进行增广,将增广后的流值回写到原网络上,再建立当前网络的辅助网络,如此反复,达到最大流。分层的目的是降低寻找增广路的代价。
算法步骤如下:
STEP1:建造原网络G的一个分层网络L。
STEP2:用增广路算法计算L的最大流F,若在L中找不到增广路,算法结束。
SETP3:根据F更新G中的流f,转STEP1。
分层网络的构造算法:
STEP1:标号源节点s,M[s]=0。
STEP2:调用广度优先遍历算法,执行一步遍历操作,当前遍历的弧e=v1v2,令r=G.u(e)-G.f(e)。
若r>0,则
(1)若M[v2]还没有遍历,则M[v2]=M[v1]+1,且将弧e加入到L中,容量L.u(e)=r。
(2)若M[v2]已经遍历且M[v2]=M[v1]+1,则将边e加入到L中,容量L.u(e)=r。
(3)否则L.u(e)=0。
否则L.u(e)=0。
重复本步直至G遍历完。其中的G.u(e)、G.f(e)、L.u(e)分别表示图G中弧e的容量上界和当前流量,图L中弧e的容量上界。
算法的时间复杂度为O(2mn)。其中m为弧的数目,是多项式算法。邻接表表示图,空间复杂度为O(n+m)。
模板有两个哦~
第一个是自己码的,可能更清晰。
#include第二个是wjw提供的真的模板:(可以这很模板)
int level[NMax];
int mkLevel() {
for(int i = (level[0] = 0) + 1; i < N; i++)level[i] = -1;
static int Q[NMax], bot;
Q[(bot = 1) - 1] = 0;
for(int top = 0; top < bot; top++) {
int x = Q[top];
for(edge *p = E[x]; p; p = p->next)if(level[p->e] == -1 && p->f)
level[Q[bot++] = p->e] = level[x] + 1;
}
return level[N - 1] != -1;
}
int extend(int a, int b) {
int r = 0, t;
if(a == N - 1)return b;
for(edge *p = E[a]; p && r < b; p = p->next)
if(p->f && level[p->e] == level[a] + 1) {
t = p->f;
if(t > b - r)t = b - r;
t = extend(p->e, t);
r += t;
p->f -= t;
OPT(p)->f += t;
}
if(!r)level[a] = -1;
return r;
}
int Dinic() {
int ret = 0, t;
while(mkLevel())while((t = extend(0, 1000000000)))ret += t;
return ret;
}我要补一个用邻接表写的:
const int INF=0x7fffffff;
int head[50000],dis[3000],f,n,m;
int IN[3000],OUT[3000];
int t,a,b,h,g,sum,ans;
struct node
{
int to,next,w;
};
node edge[50000];
void add(int u,int v,int w)
{
edge[f].to=v;
edge[f].next=head[u];
edge[f].w=w;
head[u]=f++;
edge[f].to=u;
edge[f].next=head[v];
edge[f].w=0;
head[v]=f++;
}
int bfs()
{
int i,x,v;
memset(dis,0,sizeof(dis));
dis[0]=1;
queue<int>q;
q.push(0);
while(!q.empty())
{
x=q.front();
q.pop();
for(i=head[x];i!=-1;i=edge[i].next)
{
v=edge[i].to;
if(edge[i].w&&dis[v]==0)
{
dis[v]=dis[x]+1;
if(v==n+1)return 1;
q.push(v);
}
}
}
return 0;
}
int dfs(int s,int cur_flow)
{
int i,v,tmp,dt=cur_flow;
if(s==n+1)return cur_flow;
for(i=head[s];i!=-1;i=edge[i].next)
{
v=edge[i].to;
if(edge[i].w&&dis[s]==dis[v]-1)
{
int flow=dfs(v,min(dt,edge[i].w));
edge[i].w-=flow;
edge[i^1].w+=flow;
dt-=flow;
}
}
return cur_flow-dt;
}
int dinic()
{
int tt=0;
while(bfs())
tt+=dfs(0,INF);
return tt;
} 其实最后还有一种算法叫ISAP,据说是SAP算法的IMPROVE版本,于是乎,我不准备讲了,好麻烦,直接引用吧:
网络流——ISAP详解
====================以下为引用内容====================
ISAP 算法就是不停地找最短增广路,找到之后增广;如果遇到死路就 retreat,直到发现s, t不连通,算法结束。找最短路本质上就是无权最短路径问题,因此采用 BFS 的思想。具体来说,使用一个数组d,记录每个节点到汇点t的最短距离。搜索的时候,只沿着满足d[u]=d[v]+1的边u→v(这样的边称为允许弧)走。显然,这样走出来的一定是最短路。
原图存在两种子图,一个是残量网络,一个是允许弧组成的图。残量网络保证可增广,允许弧保证最短路(时间界较优)。所以,在寻找增广路的过程中,一直是在残量网络中沿着允许弧寻找。因此,允许弧应该是属于残量网络的,而非原图的。换句话说,我们沿着允许弧,走的是残量网络(而非原图)中的最短路径。当我们找到沿着残量网络找到一条增广路,增广后,残量网络肯定会变化(至少少了一条边),因此决定允许弧的d数组要进行相应的更新(顺便提一句,Dinic 的做法就是每次增广都重新计算d数组)。然而,ISAP 「改进」的地方之一就是,其实没有必要马上更新d数组。这是因为,去掉一条边只可能令路径变得更长,而如果增广之前的残量网络存在另一条最短路,并且在增广后的残量网络中仍存在,那么这条路径毫无疑问是最短的。所以,ISAP 的做法是继续增广,直到遇到死路,才执行 retreat 操作。
说到这里,大家应该都猜到了,retreat 操作的主要任务就是更新d数组。那么怎么更新呢?非常简单:假设是从节点u找遍了邻接边也没找到允许弧的;再设一变量m,令m等于残量网络中u的所有邻接点的d数组的最小值,然后令d[u]等于m+1即可。这是因为,进入 retreat 环节说明残量网络中u和 t已经不能通过(已过时)的允许弧相连,那么u和t实际上在残量网络中的最短路的长是多少呢?(这正是d的定义!)显然是残量网络中u的所有邻接点和t的距离加1的最小情况。特殊情况是,残量网络中u根本没有邻接点。如果是这样,只需要把d[u]设为一个比较大的数即可,这会导致任何点到u的边被排除到残量网络以外。(严格来说只要大于等于∣V∣即可。由于最短路一定是无环的,因此任意路径长最大是∣V∣−1)。修改之后,只需要把正在研究的节点u沿着刚才走的路退一步,然后继续搜索即可。
讲到这里,ISAP 算法的框架内容就讲完了。对于代码本身,还有几个优化和实现的技巧需要说明。
算法执行之前需要用 BFS 初始化d数组,方法是从t到s逆向进行。算法主体需要维护一个「当前节点」u
,执行这个节点的前进、retreat 等操作。记录路径的方法非常简单,声明一个数组p,令p[i]等于增广路上到达节点i的边的序号(这样就可以找到从哪个顶点到的顶点i)。需要路径的时候反向追踪一下就可以了。
判断残量网络中s,t不连通的条件,就是d[s]≥∣V∣ 。这是因为当s,t不连通时,最终残量网络中s将没有任何邻接点,对s的 retreat 将导致上面条件的成立。
GAP 优化。
GAP 优化可以提前结束程序,很多时候提速非常明显(高达 100 倍以上)。GAP 优化是说,进入 retreat 环节后,u,t
之间的连通性消失,但如果u是最后一个和t距离d[u](更新前)的点,说明此时s,t也不连通了。这是因为,虽然u,t已经不连通,但毕竟我们走的是最短路,其他点此时到t的距离一定大于d[u](更新前),因此其他点要到t,必然要经过一个和t距离为d[u](更新前)的点。GAP 优化的实现非常简单,用一个数组记录并在适当的时候判断、跳出循环就可以了。
另一个优化,就是用一个数组保存一个点已经尝试过了哪个邻接边。寻找增广的过程实际上类似于一个 BFS 过程,因此之前处理过的邻接边是不需要重新处理的(残量网络中的边只会越来越少)。具体实现方法直接看代码就可以,非常容易理解。需要注意的一点是,下次应该从上次处理到的邻接边继续处理,而非从上次处理到的邻接边的下一条开始。
最后说一下增广过程。增广过程非常简单,寻找增广路成功(当前节点处理到t
)后,沿着你记录的路径走一遍,记录一路上的最小残量,然后从s到t更新流量即可。
====================以上为引用内容====================
#include
#include
#include
#include
using namespace std;
#define MAXN 10005
#define MAXE 200000
#define INF 1e9
int tmp,src,des,cnt;
int n,m;
struct Edge{
int from, to;
int next,cap;
}edge[MAXE];
int head[MAXN];
int gap[MAXN],dep[MAXN],cur[MAXN], stack[MAXN], top;
int ISAP()
{
int cur_fLow,max_fLow,u,insert,i;
memset(dep,0,sizeof(dep));
memset(gap,0,sizeof(gap));
memcpy(cur, head, n);
max_fLow = 0;
u = src;
top = 0;
while(dep[src] < n)
{
if(u == des)
{
cur_fLow = INF;
for(i = 0; i < top; ++i)
{
if(cur_fLow > edge[stack[i]].cap)
{
insert = i;
cur_fLow = edge[stack[i]].cap;
}
}
for(i = 0; i < top; ++i)
{
edge[stack[i]].cap -= cur_fLow;
edge[stack[i]^1].cap += cur_fLow;
}
max_fLow += cur_fLow;
u = edge[ stack[top = insert]].from;
}
for(i = cur[u]; i != -1; i = edge[i].next)
if((edge[i].cap > 0) && (dep[u] == dep[edge[i].to]+1))
break;
if(i != -1)
{
stack[top++] = i;
u = edge[i].to;
}
else
{
if(0 == --gap[dep[u]]) break;
int minn = n;
for(i = head[u]; i != -1; i = edge[i].next)
{
if(edge[i].cap > 0)
minn = (minn > dep[edge[i].to]) ? (cur[u]= i, dep[edge[i].to]) : minn;
}
++gap[dep[u] = minn + 1];
if(u != src) u = edge[stack[--top]].from;
}
}
return max_fLow;
}
void addedge(int u,int v,int f)
{
edge[cnt].next = head[u];
edge[cnt].from = u;
edge[cnt].to = v;
edge[cnt].cap = f;
head[u] = cnt++;
edge[cnt].next = head[v];
edge[cnt].from = v;
edge[cnt].to = u;
edge[cnt].cap = 0;
head[v] = cnt++;
}
int main()
{
while(scanf("%d%d",&m,&n)!=EOF)
{
cnt=0;
src = 0;
des = n-1;
memset(head,-1,sizeof(head));
while(m--)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
--a, --b;
addedge(a, b, c);
//addedge(b, a, c);如果是无向边的加上这句
}
int ans=ISAP();
printf("%d\n",ans);
}
return 0;
} 这就是传说中的ISAP,据说效率比Dinic还高诶!
还有个更变态的预流推进:
预流推进算法给每一个顶点一个标号h(v),表示该点到t的最短路(在残量网络中)。
第一步hights()过程,就是BFS出初始最短路,计算出每一个结点的h(v)。//可以看作是汇点有“吸力”,使每个结点有不同的负压,在“负压”作用下把来自源点的流吸过去。
预流推进算法的特征是运用了预流来加快运算。预流说明图中的结点(除s, t),仅需要满足流入量 >= 流出量。其中流入量>流出量的结点,我们称之为活动结点。/换句话说就是有流可吸,还没吸到地方。/我们的算法就是不断地将活动结点,变为非活动结点,使得预流成为可行流。
算法过程prepare(),即首先将与s相连的边设为满流,并将这时产生的活动结点加入队列Q。这是算法的开始。
以后便重复以下过程直到Q为空:
(1).选出Q的一个活动结点u。并依次判断残量网络G’中每条边(u, v),若h(u) = h(v) + 1,则顺着这些边推流,直到Q变成非活动结点(不存在多余流量)。(Push推流过程)//同时把所有v加入活动结点的队列。
(2).如果u还是活动结点。则需要对u进行重新标号:h(u) = min{h(v) + 1},其中边(u,v)存在于G’ 中。然后再将u加入队列。(reCalc过程)//后面都满流时就吸不动了,负压自然也要重新计算。
可以证明,通过以上算法得到的结果就是最大流。
//显然每次循环后标号和残量网络都是相容的。算法结束时Q为空,只可能是没有活动结点。因为一开始就把从源所有的流推了出来,只可能是要么能够推到汇要么最后退回源。显然,一开始源的标号最高,退回源说明源汇之间已被切断,否则总能杀出一条增广路来。
如果该算法的Q是标准的FIFO队列,则时间复杂度为(n2m),/最高标号不会超过n(超过时必无到汇的路径),所以n个点每个最多重新标号n次,两次标号之间m条边每条最多推流一次。/如果是优先队列,并且标号最高的点优先的话,我们就得到了最高标号预流推进算法,其时间复杂度仅为(n2sqrt(m)),/复杂度分析进行中……/算是比较快的最大流算法了。
模板题转自这里
#include
#include
#define DEBUG
#ifdef DEBUG
#define debug(...) printf( __VA_ARGS__)
#else
#define debug(...)
#endif
#define N 102
#define MAX_INT 2000000
#define min(a, b) ((a) < (b) ? (a) : (b))
int graph[N][N];
int h[N];
int e[N];
int n;
int push_relabel(int s, int t)
{
int max_flow, u, v, d, done, relabel, min_height;
memset(h, 0, sizeof(h));
memset(e, 0, sizeof(e));
h[s] = n;
for (u = 1; u <= t; u++) {
if (graph[s][u] > 0) {
e[u] = graph[s][u];
e[s] -= graph[s][u];
graph[u][s] = graph[s][u];
graph[s][u] = 0;
}
}
for (;;) {
done = 1;
for (u = s+1; u < t; u++) {
if (e[u] > 0) {
done = 0;
//先假设顶点u需要relabel
relabel = 1;
for (v = s; v <= t && e[u] > 0; v++) { /* 检查能push的顶点 */
if (graph[u][v] > 0 && h[u] > h[v]) {
//push
relabel = 0;
d = min(graph[u][v], e[u]);
e[u] -= d;
e[v] += d;
graph[u][v] -= d;
graph[v][u] += d;
debug("push %d --%d--> %d, e[%d] = %d\n", u, d, u, u, e[u]);
}
}
//没有可以push的顶点,执行relabel
if (relabel) {
//relabel
min_height = MAX_INT;
for (v = s; v <= t; v++) {
if (graph[u][v] > 0 && h[v] < min_height) {
min_height = h[v];
}
}
h[u] = 1 + min_height;
debug("relabel %d height to %d\n", u, h[u]);
}
}
}
if (done) { /* 除源点和汇点外,每个顶点的e[i]都为0 */
max_flow = 0;
for (u = s; u <= t; u++) {
if (graph[t][u] > 0) {
max_flow += graph[t][u];
}
}
break;
}
}
return max_flow;
}
int main()
{
int np, nc, m, u, v, w;
while (scanf("%d", &n) != EOF) {
n += 2; /* 添加源点和汇点 */
scanf("%d %d %d", &np, &nc, &m);
memset(graph, 0, sizeof(graph));
//输入m条边
while (m--) {
scanf(" (%d,%d)%d", &u, &v, &w);
graph[u+1][v+1] = w;
}
//输入np个power station
while (np--) {
scanf(" (%d)%d", &u, &w);
graph[0][u+1] = w;
}
//输入nc个consumer
while (nc--) {
scanf(" (%d)%d", &u, &w);
graph[u+1][n-1] = w;
}
printf("%d\n", push_relabel(0, n-1));
}
return 0;
} 哈利路亚~真tm!!!!!神坑~~!!!!