逆序对的求解&应用

先来看一下什么是逆序对
逆序对的定义
设 A 为一个有 n 个数字的有序集 (n>1)，其中所有数字各不相同。
如果存在正整数 i, j 使得 1 ≤ i < j ≤ n 而且 A[i] > A[j]，则 这个有序对称为 A 的一个逆序对，也称作逆序数。

简单来说，就是一个数的前面有几个比它大的数，那么这个数就有几对逆序对。
接下来介绍两种求逆序对的方法 暴力的解法就不说了

归并排序
为什么会想到归并排序呢，首先在归并排序中，每一个分块中的数字都是单调的，因此我们可以轻松求出逆序对的数量时间复杂度O(NlogN)，下面图片解释一下。

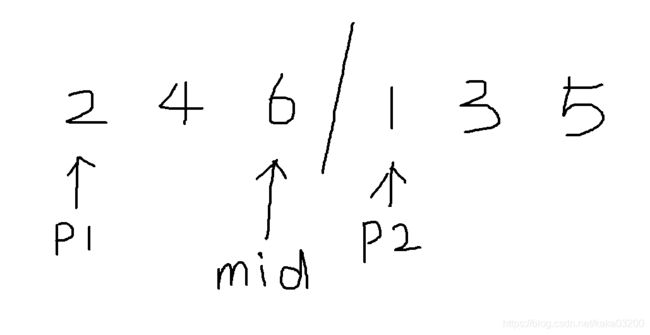
当p2指针所指的数小于p1所指的数时，那么p1及p1右侧的数都大于p2所指的数，因此当前的逆序对数量为mid - p1+1

#include 
using namespace std;
const int N = 100010;
int a[N], tmp[N];
int n, ans;
void merge_sort(int l, int mid, int r) {
	int fl = l;
	int sl = mid + 1;
	int index = l;
	while (fl <= mid && sl <= r) {
		if (a[fl] <= a[sl]) tmp[index++] = a[fl++];
		else tmp[index++] = a[sl++], ans += mid - fl + 1;
	}

	while (fl <= mid) tmp[index++] = a[fl++];

	while (sl <= r) tmp[index++] = a[sl++];

	for (int i = l; i <= r; i++) a[i] = tmp[i];

}

void merge(int l, int r) {
	
	if (l < r) {
		int mid = (l + r) / 2;
		merge(l, mid);
		merge(mid + 1, r);
		merge_sort(l, mid, r);
	}
}

int main() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> a[i];
	merge(1, n);

	cout << ans;
}

树状数组
利用树状数组单点修改和区间查询的性质，每次我们插入一个数字的值 add（x, 1），代表x数值出现了一次，然后利用区间求和的方法可以求出x之前包括x的数的个数求出来，这样算出的个数显然是小于等于x的值的个数，因此我们求大于x的个数只要用当前已经插入的个数i减去x前面的个数即可，即 i - get(x)，这样就完成了。当然，如果数值过大导致数组无法存下或时间复杂度过大时，可以先离散化数值再求解。

#include 
using namespace std;
const int N = 100010;
int c[N];
inline int lowbit(int x) {
	return x & -x;
}

void add(int x, int k) {
	for (int i = x; i <= N; i += lowbit(i))
		c[i] += k;
}

int get(int x) {
	int res = 0;
	for (int i = x; i > 0; i -= lowbit(i))
		res += c[i];
	return res;
}

int main() {
	int n;
	cin >> n;
	for (int i = 1; i <= n; i++) {
		int x;
		cin >> x;
		add(x, 1);
		cout << i - get(x) << " ";
	}
}

最后，逆序对有什么用呢？

逆序对可以用来求解冒泡排序的最小交换次数，如果采用普通的冒泡排序，显然复杂度为O(N²)的，如果用逆序对求解则为O(NlogN)