2019年ACM ICPC西安邀请赛赛后总结及部分题解
A题 温暖的签到题,一眼秒了
L题 第二个就开了L题,因为看上去是个打表,写了个bfs打表,发现规律和%4的余数有关(1,3要特判),31分钟1A
此时队友给我读了D和M题,我去开D,他们写M。然而他们拒绝了我的二分,非要写最短路。然后半小时后发现算法假了,在我苦苦哀求之下写了二分+bfs
M题 二分升级次数,假设二分到mid,边权小于mid*d的可以通过,否则不能通过,总共可以通过mid*e条边。那就相当于是一个边权为1的最短路,问1到n的距离是否小于等于mid*e。既然边权都为1了,直接线性的bfs就行了。 87分钟1A
D题队友不告诉我每个数字都能被100整除。。。我赛后才知道。。。每个数字能整除100,那大小就是500,200个数字,开个200*1e5的DP数组即可。事实上在赛前一天热身赛回去的路上为了解乏我随便出了一道题(和这个题一模一样)给大家做。然后大家都会DP了。
整理一下思路:设A为第一个人最终的分数,B为第二个人最终的分数。先bfs把图01染色,然后算出被染成1的点之和 与 被染成0的点之和 的差值。对于某一差值x,可以给A或者给B,也就是使A-B的值增加x或者减少x。(DP的两种转移)DP的值为1时代表存在这种状态,否则不存在。最后从小到大枚举,直到找到一个DP值为1的地方(即存在这个差值)为最小差值。
然而我不知道数字能被100整除,就上了离散化背包,用set存储。先01染色将集合求出来,初始set塞入0代表刚开始差值为0,每次取set的值,将下一位塞入当前值+x和当前值-x即可。然后剪枝了一下,先将差值从大到小排序,如果当前set里的值大于后缀和,那么就直接减去后缀和再跳出。保证不会超时。复杂度约为n³?玄学,不懂。
由于数组没清零wa了一发,144分钟2A。(如果不用离散化背包的话,那我15分钟内就能过QAQ)
下面是比赛AC的代码(注释是之后加的,其他都是AC了打印下来,应该没抄错吧QAQ)
#include
using namespace std;
#define pb push_back
#define mp make_pair
#define fi first
#define se second
const int maxn = 210;
sets[maxn];
vectorff[maxn];
int co[maxn], dqs[maxn], cnt = 0, ww[maxn];
//dqs存后缀和,ww存每个集合的差值
bool vis[maxn];
bool cmp(int a, int b) {
return a > b;
}
void bfs(int qwq) {
int a1 = 0;
queue >q;//pair第二维代表颜色,01两种
while(!q.empty()) q.pop();
q.push(mp(qwq,1));
vis[qwq] = 1;
while(!q.empty()) {
pair now = q.front();
q.pop();
if(now.se == 1) a1 += co[now.fi];
else a1 -= co[now.fi];
for(auto i : ff[now.fi]) {
if(vis[i]) continue;
vis[i] = 1;
q.push(mp(i, 1 - now.se));
}
}
ww[++cnt] = abs(a1);//存入集合差值
}
int main() {
int n, m, t;
cin >> t;
while(t--) {
cin >> n >> m;
int sum = 0;
cnt = 0;
memset(vis,0,sizeof vis);
memset(dqs,0,sizeof dqs);
for(int i = 1; i <= n; i++)
s[i].clear(), ff[i].clear();
for(int i = 1; i <= n; i++)
cin >> co[i], sum += co[i];
for(int i = 1; i <= m; i++) {
int a, b;
cin >> a >> b;
ff[a].pb(b);
ff[b].pb(a);
}
for(int i = 1; i <= n; i++)
if(!vis[i]) bfs(i);//找连通块
sort(ww+1, ww+1+cnt, cmp);
for(int i = cnt; i >= 1; i--)
dqs[i] = dqs[i+1] + ww[i];
s[1].insert(0);
for(int i = 1; i <= cnt; i++) {
set::iterator it;
for(it = s[i].begin(); it != s[i].end(); it++) {
if(*it >= dqs[i]) { //大于后缀和,那么减去后缀和直接break
s[cnt+1].insert(*it - dqs[i]);
break;
}
}
s[i+1].insert(*it + ww[i]);//转移1,加上当前值
if(abs(*it) > dqs[i]) { //小于前缀和,就加上前缀和然后下一步
s[cnt+1].insert(dqs[i] + *it);
continue;
}
s[i+1].insert(*it - ww[i]);//转移2,减去当前值
}
set::iterator it;
int minn = 1e9;
for(it = s[cnt+1].begin(); it != s[cnt+1].end(); it++)
minn = min(minn, abs(*it));
cout << (sum - minn)/2 + minn << endl;
}
} 第一次写离散化背包,调试了好久,所以才那么慢过。当时还在纳闷怎么全场都会这个离散化背包,原来是能整除100啊QAQ。如果不能整除的话我这个代码应该是也能过的。这招是我当时寒假camp偷学的div1Claris哥哥的DP讲课视频,希望没学错。(如果下面有个大佬出来告诉我我算法假了那就很尴尬)
毕竟我读不懂题是个梗,希望下次队友不要给我加大难度了呜呜呜。
C题是个简单几何,然而我们队没人会几何。不像M题他们不二分我还能喷人(其实并不敢喷队友爸爸),这个几何我也不会,看着他们疯狂wa也没什么办法。他们怀疑精度问题,于是我把圆周率给他们背了十几位(实际当然是算法假了),然后整了好久才过。 171分钟 3A
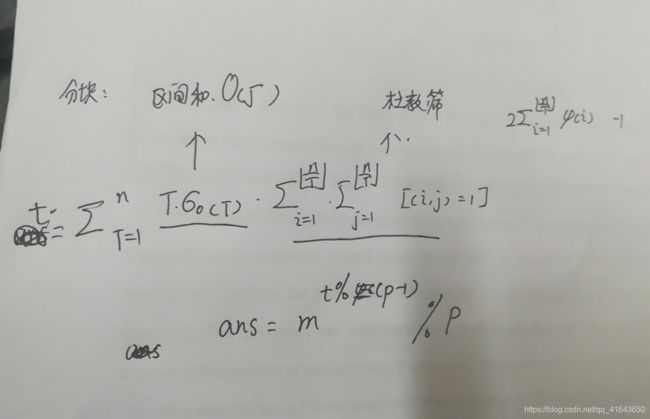
B题是一道全场362支队伍只过了3支队伍的神仙题,然而我们队是其中之一。感谢数论king神仙队友,欧拉降幂+杜教筛,搞了一个多小时,246分钟 1A
6题拿金,感觉还是不错的。
赛后补下题
E题树链剖分,分析一下nim博弈的性质,知道操作3就是一个全部异或。那么按位拆分,开30棵线段树即可。
H题先差分前缀和算出最终的形态及连通块数量,然后倒着做,修改的块数是3e7,要求线性做,那就是并查集维护删除,如果删除后两边联通,就修改答案即可。是道大模拟。
J题人均过,但是我不会,我好菜啊