Andres_Lionel
Andres_Lionel

XOR TREE【牛客练习赛58 F】【树链剖分】

题目链接

 这个问题很容易想到之间的关系，假设现在所要查询的这条链上有V1、V2、…… VK个点，那么第i个点的贡献在抑或中出现的次数XOR为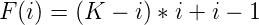\large F(i) = (K - i) * i + i - 1

  • 当K为偶数时候，F(i)恒定为奇数
  • 当K为奇数的时候，F(i)在i为偶数的时候F(i)为奇数
  • 只有F(i)为奇数的时候，在抑或XOR中才有作用

  于是，如果K为偶数的时候，我们直接求这条链上所有值的抑或XOR和即可，树链剖分就可以很好的维护了。

  如果K为奇数的时候，我们需要求第2、4、6、……这几个偶数点的抑或XOR和。如果我们直接在线段树上维护当然是不行的，因为dfs序号是没有这样的独立性的，可能会有两个同时为偶数dfs序的点却是连接在一起的。

  所以考虑深度，会发现，深度奇偶不同的点一定是不相连接的，并且中间只隔了一个点。于是，我们这里开两个线段树，维护一下每个奇偶深度的抑或XOR和。

  这样，我们查询的时候，只用查询于两个结点的deep的奇偶不同的点的抑或和即可。

  因为是奇数个点，所以也代表了两个查询结点一定是在深度上同奇偶。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
//#include 
//#include 
#define lowbit(x) ( x&(-x) )
#define pi 3.141592653589793
#define e 2.718281828459045
#define INF 0x3f3f3f3f3f3f3f3f
#define eps 1e-8
#define HalF (l + r)>>1
#define lsn rt<<1
#define rsn rt<<1|1
#define Lson lsn, l, mid
#define Rson rsn, mid+1, r
#define QL Lson, ql, qr
#define QR Rson, ql, qr
#define myself rt, l, r
#define MP(a, b) make_pair(a, b)
#define MAX_3(a, b, c) max(a, max(b, c))
#define Rabc(x) x > 0 ? x : -x
using namespace std;
typedef unsigned long long ull;
typedef unsigned int uit;
typedef long long ll;
inline int read()
{
    int x=0; char c=getchar();
    while(c<'0'||c>'9') c=getchar();
    while(c>='0'&&c<='9') { x=(x<<1)+(x<<3)+c-'0'; c=getchar(); }
    return x;
}
const int maxN = 2e5 + 7;
int N, Q, a[maxN], head[maxN], cnt;
struct Eddge
{
    int nex, to;
    Eddge(int a=-1, int b=0):nex(a), to(b) {}
}edge[maxN << 1];
inline void addEddge(int u, int v)
{
    edge[cnt] = Eddge(head[u], v);
    head[u] = cnt++;
}
inline void _add(int u, int v) { addEddge(u, v); addEddge(v, u); }
int siz[maxN], deep[maxN], Wson[maxN], fa[maxN];
void dfs_1(int u, int father)
{
    fa[u] = father; deep[u] = deep[father] + 1; Wson[u] = 0; siz[u] = 1;
    int maxx = 0;
    for(int i=head[u], v; ~i; i=edge[i].nex)
    {
        v = edge[i].to;
        if(v == father) continue;
        dfs_1(v, u);
        siz[u] += siz[v];
        if(maxx < siz[v])
        {
            maxx = siz[v];
            Wson[u] = v;
        }
    }
}
int top[maxN], dfn[maxN], tot, rid[maxN];
void dfs_2(int u, int topy)
{
    top[u] = topy;
    dfn[u] = ++tot; rid[tot] = u;
    if(Wson[u]) dfs_2(Wson[u], topy);
    for(int i=head[u], v; ~i; i=edge[i].nex)
    {
        v = edge[i].to;
        if(v == fa[u] || v == Wson[u]) continue;
        dfs_2(v, v);
    }
}
int tree[maxN << 2][3] = {0};
inline void pushup(int rt)
{
    tree[rt][2] = tree[lsn][2] ^ tree[rsn][2];
    tree[rt][0] = tree[lsn][0] ^ tree[rsn][0];
    tree[rt][1] = tree[lsn][1] ^ tree[rsn][1];
}
void buildTree(int rt, int l, int r)
{
    if(l == r)
    {
        tree[rt][deep[rid[l]] & 1] = a[rid[l]];
        tree[rt][2] = a[rid[l]];
        return;
    }
    int mid = HalF;
    buildTree(Lson); buildTree(Rson);
    pushup(rt);
}
void update(int rt, int l, int r, int qx, int val)
{
    if(l == r) { tree[rt][deep[rid[l]] & 1] = val; tree[rt][2] = val; return; }
    int mid = HalF;
    if(qx <= mid) update(Lson, qx, val);
    else update(Rson, qx, val);
    pushup(rt);
}
int s[3] = {0};
void query(int rt, int l, int r, int ql, int qr)
{
    if(ql <= l && qr >= r)
    {
        s[0] ^= tree[rt][0];
        s[1] ^= tree[rt][1];
        s[2] ^= tree[rt][2];
        return;
    }
    int mid = HalF;
    if(qr <= mid) query(QL);
    else if(ql > mid) query(QR);
    else { query(QL); query(QR); }
}
inline int _LCA(int u, int v)
{
    while(top[u] ^ top[v])
    {
        if(deep[top[u]] < deep[top[v]]) swap(u, v);
        u = fa[top[u]];
    }
    if(deep[u] > deep[v]) swap(u, v);
    return u;
}
inline int Range_Query(int u, int v)
{
    int ans = 0, lca = _LCA(u, v), len, op = (deep[u] & 1) ^ 1;
    int dis = deep[u] + deep[v] - 2 * deep[lca] + 1; dis &= 1;
    if(dis)
    {
        while(top[u] ^ top[v])
        {
            if(deep[top[u]] < deep[top[v]]) swap(u, v);
            len = deep[u] - deep[top[u]] + 1; len &= 1;
            s[0] = s[1] = s[2] = 0;
            query(1, 1, N, dfn[top[u]], dfn[u]);
            ans ^= s[op];
            u = fa[top[u]];
        }
        if(deep[u] < deep[v]) swap(u, v);
        len = deep[u] - deep[v] + 1; len &= 1;
        s[0] = s[1] = s[2] = 0;
        query(1, 1, N, dfn[v], dfn[u]);
        ans ^= s[op];
    }
    else
    {
        s[2] = 0;
        while(top[u] ^ top[v])
        {
            if(deep[top[u]] < deep[top[v]]) swap(u, v);
            query(1, 1, N, dfn[top[u]], dfn[u]);
            u = fa[top[u]];
        }
        if(deep[u] < deep[v]) swap(u, v);
        query(1, 1, N, dfn[v], dfn[u]);
        ans = s[2];
    }
    return ans;
}
inline void init()
{
    cnt = tot = 0;
    for(int i=1; i<=N; i++) head[i] = -1;
}
int main()
{
    N = read(); Q = read();
    init();
    for(int i=1; i<=N; i++) a[i] = read();
    for(int i=1, u, v; i

 

你可能感兴趣的:(树链剖分,数据结构,线段树)

  • 数组去重 好奇的猫猫猫
    整理自js中基础数据结构数组去重问题思考？如何去除数组中重复的项例如数组：[1,3,4,3,5]我们在做去重的时候，一开始想到的肯定是，逐个比较，外面一层循环，内层后一个与前一个一比较，如果是久不将当前这一项放进新的数组，挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低，代码量还多，思考？有没有更好的方法这时候不禁一想当然有了！！！hashtable啊，通过对象的hash办法
  • 回溯算法-重新安排行程 chirou_ 算法数据结构图论c++图搜索
    leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
  • Redis系列：Geo 类型赋能亿级地图位置计算 Ly768768 redisbootstrap数据库
    1前言我们在篇深刻理解高性能Redis的本质的时候就介绍过Redis的几种基本数据结构，它是基于不同业务场景而设计的：动态字符串(REDIS_STRING)：整数(REDIS_ENCODING_INT)、字符串(REDIS_ENCODING_RAW)双端列表(REDIS_ENCODING_LINKEDLIST)压缩列表(REDIS_ENCODING_ZIPLIST)跳跃表(REDIS_ENCODI
  • Faiss：高效相似性搜索与聚类的利器 网络·魚 大数据faiss
    Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
  • 数据结构之哈希表 X同学的开始 数据结构数据结构散列表
    哈希表(散列表)出现的原因在顺序表中查找时，需要从表头开始，依次遍历比较a[i]与key的值是否相等，直到相等才返回索引i；在有序表中查找时，我们经常使用的是二分查找，通过比较key与a[i]的大小来折半查找，直到相等时才返回索引i。最终通过索引找到我们要找的元素。但是，这两种方法的效率都依赖于查找中比较的次数。我们有一种想法，能不能不经过比较，而是直接通过关键字key一次得到所要的结果呢？这时，
  • Python开发常用的三方模块如下： 换个网名有点难 python开发语言
    Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
  • 数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列C语言
    文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
  • [Python] 数据结构 详解及代码 AIAdvocate 算法python数据结构链表
    今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
  • 4.C_数据结构_队列 荣世蓥 数据结构数据结构
    概述什么是队列：队列是限定在两端进行插入操作和删除操作的线性表。具有先入先出(FIFO)的特点相关名词：队尾：写入数据的一段队头：读取数据的一段空队：队列中没有数据，队头指针=队尾指针满队：队列中存满了数据，队尾指针+1=队头指针循环队列1、基本内容循环队列是以数组形式构成的队列数据结构。循环队列的结构体如下：typedefintdata_t;//队列数据类型#defineN64//队列容量typ
  • C++八股 Petrichorzncu 八股总结c++开发语言
    这里写目录标题C++内存管理C++的构造函数，复制构造函数，和析构函数深复制与浅复制：构造函数和析构函数哪个能写成虚函数，为什么？C++数据结构内存排列结构体和类占用的内存：==虚函数和虚表的原理==虚函数虚表（Vtable）虚函数和虚表的实现细节==内存泄漏==指针的工作原理函数的传值和传址new和delete与malloc和freeC++内存区域划分C++11新特性C++常见新特性==智能指针
  • 【树一线性代数】005入门 Owlet_woodBird 算法
    Index本文稍后补全，推荐阅读：https://blog.csdn.net/weixin_60702024/article/details/141874376分析实现总结本文稍后补全，推荐阅读：https://blog.csdn.net/weixin_60702024/article/details/141874376已知非空二叉树T的结点值均为正整数，采用顺序存储方式保存，数据结构定义如下:t
  • python获取子进程返回值_Python对进程Multiprocessing子进程返回值 weixin_39752157 python获取子进程返回值
    在实际使用多进程的时候，可能需要获取到子进程运行的返回值。如果只是用来存储，则可以将返回值保存到一个数据结构中；如果需要判断此返回值，从而决定是否继续执行所有子进程，则会相对比较复杂。另外在Multiprocessing中，可以利用Process与Pool创建子进程，这两种用法在获取子进程返回值上的写法上也不相同。这篇中，我们直接上代码，分析多进程中获取子进程返回值的不同用法，以及优缺点。初级用法
  • 【数据结构-一维差分】力扣2848. 与车相交的点 hlc@ 数据结构数据结构leetcode算法
    给你一个下标从0开始的二维整数数组nums表示汽车停放在数轴上的坐标。对于任意下标i，nums[i]=[starti,endi]，其中starti是第i辆车的起点，endi是第i辆车的终点。返回数轴上被车任意部分覆盖的整数点的数目。示例1：输入：nums=[[3,6],[1,5],[4,7]]输出：7解释：从1到7的所有点都至少与一辆车相交，因此答案为7。示例2：输入：nums=[[1,3],[5
  • JavaScript `Map` 和 `WeakMap`详细解释 跳房子的前端 JavaScript原生方法javascript前端开发语言
    在JavaScript中，Map和WeakMap都是用于存储键值对的数据结构，但它们有一些关键的不同之处。MapMap是一种可以存储任意类型的键值对的集合。它保持了键值对的插入顺序，并且可以通过键快速查找对应的值。Map提供了一些非常有用的方法和属性来操作这些数据对：set(key,value):将一个键值对添加到Map中。如果键已经存在，则更新其对应的值。get(key):获取指定键的值。如果键
  • 【高阶数据结构】并查集 椿融雪 数据结构与算法数据结构并查集
    文章目录一、并查集原理二、并查集实现三、并查集应用一、并查集原理在一些应用问题中，需要将n个不同的元素划分成一些不相交的集合。开始时，每个元素自成一个单元素集合，然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-findset)。比如：某公司今年校招全国总共招生10人，西安招4人，成都招3人，
  • python中文版软件下载-Python中文版 编程大乐趣
    python中文版是一种面向对象的解释型计算机程序设计语言。python中文版官网面向对象编程，拥有高效的高级数据结构和简单而有效的方法，其优雅的语法、动态类型、以及天然的解释能力，让它成为理想的语言。软件功能强大，简单易学，可以帮助用户快速编写代码，而且代码运行速度非常快，几乎可以支持所有的操作系统，实用性真的超高的。python中文版软件介绍：python中文版的解释器及其扩展标准库的源码和编
  • 开发游戏的学习规划 杰克逊的日记 游戏学习
    第一阶段：●C#语言快速系统地学习一遍（基础的语法、面向对象、基础的数据结构、基础的设计模式）●Unity的2D和3D部分及UI、动画、物理系统●阶段性测验：需要去用前面所学的这些基础知识来完成一个简单的2d或者3d的案例，将通过一个自制的《Flappybird》游戏案例讲解游戏开发的思想及方法，并将《Flappybird》这个游戏进一步改造成一个横版射击类游戏《Crazybird》以巩固并且升华
  • 六、全局锁和表锁：给表加个字段怎么有这么多阻碍 nieniemin
    数据库锁设计的初衷是处理并发问题。作为多用户共享的资源，当出现并发访问的时候，数据库需要合理地控制资源的访问规则。而锁就是用来实现这些访问规则的重要数据结构。根据加锁的范围，MySQL里面的锁大致可以分成全局锁、表级锁和行锁三类。6.1全局锁全局锁就是对整个数据库实例加锁。MySQL提供了一个加全局读锁的方法，命令是Flushtableswithreadlock(FTWRL)。当你需要让整个库处于
  • Golang Channel PandaSkr golang
    Channel解析1.Channel源码分析1.1Channel数据结构typehchanstruct{qcountuint//channel的元素数量dataqsizuint//channel循环队列长度bufunsafe.Pointer//指向循环队列的指针elemsizeuint16//元素大小closeduint32//channel是否关闭0-未关闭elemtype*_type//元素类
  • ⭐算法入门⭐《归并排序》简单01 —— LeetCode 21. 合并两个有序链表 英雄哪里出来 《LeetCode算法全集》算法数据结构链表c++归并排序
    饭不食，水不饮，题必须刷C语言免费动漫教程，和我一起打卡！《光天化日学C语言》LeetCode太难？先看简单题！《C语言入门100例》数据结构难？不存在的！《数据结构入门》LeetCode太简单？算法学起来！《夜深人静写算法》文章目录一、题目1、题目描述2、基础框架3、原题链接二、解题报告1、思路分析2、时间复杂度3、代码详解三、本题小知识一、题目1、题目描述  将两个不降序链表合并为一个新的不降
  • 数据结构 1 五花肉村长 数据结构算法开发语言c语言visualstudio
    1.什么是数据结构数据结构（DataStructure）是计算机存储和组织数据的方式，是指相互之间存在的一种或多种特定关系的数据元的集合。2.什么是算法算法（Algorithm）就是定义良好的计算过程，他取一个或一组的值为输入，并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤，用来将输入数据转化成输出结果。3.数据结构和算法的书籍资料学习完数据结构知识，可以去看《剑指offer》和《
  • 【数据结构和算法实践-树-LeetCode113-路径总和Ⅱ】 NeVeRMoRE_2024 数据结构与算法实践数据结构算法leetcodeb树
    数据结构和算法实践-树-LeetCode113-路径总和Ⅱ题目MyThought代码示例JAVA-8题目给你二叉树的根节点root和一个整数目标和targetSum，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。叶子节点是指没有子节点的节点输入：root=[5,4,8,11,null,13,4,7,2,null,null,5,1],targetSum=22输出：[[5,4,11,2],[
  • 【Python】数据结构,链表,算法详解 AIAdvocate python数据结构链表排序算法广度优先深度优先
    今日内容大纲介绍自定义代码-模拟链表删除节点查找节点算法入门-排序类的冒泡排序选择排序插入排序快速排序算法入门-查找类的二分查找-递归版二分查找-非递归版分线性结构-树介绍基本概述特点和分类自定义代码-模拟二叉树1.自定义代码-模拟链表完整版"""案例:自定义代码,模拟链表.​背景: 顺序表在存储数据的时候,需要使用到连续的空间,如果空间不够,就会导致扩容失败,针对于这种情况,我们可以通过链表实现
  • AI教你学Python 第4天：函数和模块 凡人的AI工具箱 AI教你学Pythonpython开发语言人工智能AIGC
    第四天：数据结构一、什么是数据结构？数据结构是计算机科学中用于组织和存储数据的特定方式。良好的数据结构能够提高数据的访问效率、修改频率和管理能力。Python提供了多种内置数据结构，如列表、元组、字典和集合，便于开发者更有效地处理数据。二、Python中的基本数据结构1.列表（List）定义：列表是一个有序的可变集合，允许重复元素。使用方括号[]表示。#示例：定义一个列表fruits=['appl
  • 互联网 Java 工程师面试题（Java 面试题四） 苹果酱0567 面试题汇总与解析java中间件开发语言springboot后端
    下面列出这份Java面试问题列表包含的主题多线程，并发及线程基础数据类型转换的基本原则垃圾回收（GC）Java集合框架数组字符串GOF设计模式SOLID抽象类与接口Java基础，如equals和hashcode泛型与枚举JavaIO与NIO常用网络协议Java中的数据结构和算法正则表达式JVM底层Java最佳实JDBCDate,Time与CalendarJava处理XMLJUnit编程现在是时候给
  • C# Tuple、ValueTuple 語衣 C#知识补充c#
    栏目总目录TupleTuple是C#4.0引入的一个新特性，主要用于存储一个固定数量的元素序列，且这些元素可以具有不同的类型。Tuple是一种轻量级的数据结构，非常适合用于临时存储数据，而无需定义完整的类或结构体。优点简便性：可以快速创建一个包含多个不同类型数据的对象，而无需定义新的类或结构体。灵活性：元素数量和类型在编译时确定，但可以在不同上下文中重复使用不同元素的Tuple。缺点性能：作为引用
  • Rust中的所有权和借用规则详解 代码云1 rust开发语言后端
    Rust是一种系统编程语言，其设计目标包括内存安全、并发安全以及性能。为了实现这些目标，Rust引入了一系列独特的编程概念，其中最为核心的就是所有权（Ownership）和借用（Borrowing）规则。本文将详细解释Rust中的所有权和借用规则，以及它们如何确保内存安全和并发安全。一、所有权规则在Rust中，每一个值都有一个与之关联的所有者。这个所有者可以是变量、数据结构或者是其他形式的存储。所
  • BZOJ 五月胡乱补题 nike0good 其他屯题bzoj博客补档
    旧博客搬运部分格式还没来得及改T_T【BZOJ4806:炮】同BZOJ1801【BZOJ3242:[Noi2013]快餐店】树形dp，要么最远点在同一颗树上（dp），要么在不同树上，此时答案=去掉任何一条边后形成的树的答案的最小值，我们枚举去掉的那条边。由于答案=s[i]-s[j]+dis[i]+dis[j]，i，j可以分开考虑，也可以用线段树解决。【BZOJ4878:[Lydsy2017年5月月
  • 二叉树--python 电子海鸥 Python数据结构与算法python开发语言数据结构
    二叉树一、概述1、介绍是一种非线性数据结构，将数据一分为二，代表根与叶的派生关系，和链表的结构类似，二叉树的基本单元是结点，每个节点包括值和左右子节点引用。每个节点都有两个引用（类似于双向链表），分别指向左子节点和右子节点，该节点被称为这两个子节点的父节点。当给定一个二叉树的结点时，我们将在该节点的左子节点以及其以下结点所形成的树称为左子树，同理，右子节点的部分被称为右子树。在二叉树中，除了叶节点
  • 使用WAF防御网络上的隐蔽威胁之反序列化攻击 baiolkdnhjaio 网络安全
    什么是反序列化反序列化是将数据结构或对象状态从某种格式转换回对象的过程。这种格式通常是二进制流或者字符串（如JSON、XML），它是对象序列化（即对象转换为可存储或可传输格式）的逆过程。反序列化的安全风险反序列化的安全风险主要来自于处理不受信任的数据源时的不当反序列化。如果应用程序反序列化了恶意构造的数据，攻击者可能能够执行代码、访问敏感数据、进行拒绝服务攻击等。这是因为反序列化过程中可能会自动触
  • 多线程编程之join()方法 周凡杨 javaJOIN多线程编程线程
    现实生活中，有些工作是需要团队中成员依次完成的，这就涉及到了一个顺序问题。现在有T1、T2、T3三个工人，如何保证T2在T1执行完后执行，T3在T2执行完后执行？问题分析：首先问题中有三个实体，T1、T2、T3， 因为是多线程编程，所以都要设计成线程类。关键是怎么保证线程能依次执行完呢？   Java实现过程如下： public class T1 implements Runnabl
  • java中switch的使用 bingyingao javaenumbreakcontinue
    java中的switch仅支持case条件仅支持int、enum两种类型。 用enum的时候，不能直接写下列形式。 switch (timeType) { case ProdtransTimeTypeEnum.DAILY: break; default: br
  • hive having count 不能去重 daizj hive去重having count计数
    hive在使用having count()是，不支持去重计数   hive (default)> select imei from t_test_phonenum where ds=20150701 group by imei having count(distinct phone_num)>1 limit 10;  FAILED: SemanticExcep
  • WebSphere对JSP的缓存 周凡杨 WAS JSP 缓存
          对于线网上的工程，更新JSP到WebSphere后，有时会出现修改的jsp没有起作用，特别是改变了某jsp的样式后，在页面中没看到效果，这主要就是由于websphere中缓存的缘故，这就要清除WebSphere中jsp缓存。要清除WebSphere中JSP的缓存，就要找到WAS安装后的根目录。        现服务
  • 设计模式总结 朱辉辉33 java设计模式
    1.工厂模式   1.1 工厂方法模式 (由一个工厂类管理构造方法)      1.1.1普通工厂模式(一个工厂类中只有一个方法)      1.1.2多工厂模式(一个工厂类中有多个方法)      1.1.3静态工厂模式(将工厂类中的方法变成静态方法) &n
  • 实例：供应商管理报表需求调研报告 老A不折腾 finereport报表系统报表软件信息化选型
    引言 随着企业集团的生产规模扩张，为支撑全球供应链管理，对于供应商的管理和采购过程的监控已经不局限于简单的交付以及价格的管理，目前采购及供应商管理各个环节的操作分别在不同的系统下进行，而各个数据源都独立存在，无法提供统一的数据支持；因此，为了实现对于数据分析以提供采购决策，建立报表体系成为必须。 业务目标 1、通过报表为采购决策提供数据分析与支撑 2、对供应商进行综合评估以及管理，合理管理和
  • mysql 林鹤霄
    转载源：http://blog.sina.com.cn/s/blog_4f925fc30100rx5l.html mysql -uroot -p ERROR 1045 (28000): Access denied for user 'root'@'localhost' (using password: YES)   [root@centos var]# service mysql
  • Linux下多线程堆栈查看工具(pstree、ps、pstack) aigo linux
    原文：http://blog.csdn.net/yfkiss/article/details/6729364   1. pstree pstree以树结构显示进程$ pstree -p work | grep adsshd(22669)---bash(22670)---ad_preprocess(4551)-+-{ad_preprocess}(4552)  &n
  • html input与textarea 值改变事件 alxw4616 JavaScript
    // 文本输入框(input) 文本域(textarea)值改变事件 // onpropertychange(IE) oninput(w3c) $('input,textarea').on('propertychange input', function(event) {      console.log($(this).val()) });  
  • String类的基本用法 百合不是茶 String
      字符串的用法;     // 根据字节数组创建字符串 byte[] by = { 'a', 'b', 'c', 'd' }; String newByteString = new String(by);         1,length()  获取字符串的长度     &nbs
  • JDK1.5 Semaphore实例 bijian1013 javathreadjava多线程Semaphore
    Semaphore类        一个计数信号量。从概念上讲，信号量维护了一个许可集合。如有必要，在许可可用前会阻塞每一个 acquire()，然后再获取该许可。每个 release() 添加一个许可，从而可能释放一个正在阻塞的获取者。但是，不使用实际的许可对象，Semaphore 只对可用许可的号码进行计数，并采取相应的行动。 S
  • 使用GZip来压缩传输量 bijian1013 javaGZip
            启动GZip压缩要用到一个开源的Filter：PJL Compressing Filter。这个Filter自1.5.0开始该工程开始构建于JDK5.0，因此在JDK1.4环境下只能使用1.4.6。         PJL Compressi
  • 【Java范型三】Java范型详解之范型类型通配符 bit1129 java
        定义如下一个简单的范型类，   package com.tom.lang.generics; public class Generics<T> { private T value; public Generics(T value) { this.value = value; } }
  • 【Hadoop十二】HDFS常用命令 bit1129 hadoop
    1. 修改日志文件查看器   hdfs oev -i edits_0000000000000000081-0000000000000000089 -o edits.xml cat edits.xml   修改日志文件转储为xml格式的edits.xml文件，其中每条RECORD就是一个操作事务日志   2. fsimage查看HDFS中的块信息等 &nb
  • 怎样区别nginx中rewrite时break和last ronin47
    在使用nginx配置rewrite中经常会遇到有的地方用last并不能工作，换成break就可以，其中的原理是对于根目录的理解有所区别，按我的测试结果大致是这样的。 location /    {         proxy_pass http://test; 
  • java-21.中兴面试题 输入两个整数 n 和 m ，从数列 1 ， 2 ， 3.......n 中随意取几个数 , 使其和等于 m bylijinnan java
    import java.util.ArrayList; import java.util.List; import java.util.Stack; public class CombinationToSum { /* 第21 题 2010 年中兴面试题 编程求解： 输入两个整数 n 和 m ，从数列 1 ， 2 ， 3.......n 中随意取几个数 , 使其和等
  • eclipse svn 帐号密码修改问题 开窍的石头 eclipseSVNsvn帐号密码修改
    问题描述：      Eclipse的SVN插件Subclipse做得很好，在svn操作方面提供了很强大丰富的功能。但到目前为止，该插件对svn用户的概念极为淡薄，不但不能方便地切换用户，而且一旦用户的帐号、密码保存之后，就无法再变更了。 解决思路：      删除subclipse记录的帐号、密码信息，重新输入
  • [电子商务]传统商务活动与互联网的结合 comsci 电子商务
          某一个传统名牌产品，过去销售的地点就在某些特定的地区和阶层，现在进入互联网之后，用户的数量群突然扩大了无数倍，但是，这种产品潜在的劣势也被放大了无数倍，这种销售利润与经营风险同步放大的效应，在最近几年将会频繁出现。。。。        如何避免销售量和利润率增加的
  • java 解析 properties-使用 Properties-可以指定配置文件路径 cuityang javaproperties
    #mq xdr.mq.url=tcp://192.168.100.15:61618; import java.io.IOException; import java.util.Properties; public class Test { String conf = "log4j.properties"; private static final
  • Java核心问题集锦 darrenzhu java基础核心难点
    注意，这里的参考文章基本来自Effective Java和jdk源码 1)ConcurrentModificationException 当你用for each遍历一个list时，如果你在循环主体代码中修改list中的元素，将会得到这个Exception，解决的办法是： 1)用listIterator, 它支持在遍历的过程中修改元素， 2)不用listIterator, new一个
  • 1分钟学会Markdown语法 dcj3sjt126com markdown
    markdown 简明语法 基本符号 *,-,+ 3个符号效果都一样，这3个符号被称为 Markdown符号 空白行表示另起一个段落 `是表示inline代码，tab是用来标记 代码段，分别对应html的code，pre标签 换行 单一段落( <p>) 用一个空白行 连续两个空格 会变成一个 <br> 连续3个符号，然后是空行
  • Gson使用二（GsonBuilder） eksliang jsongsonGsonBuilder
    转载请出自出处：http://eksliang.iteye.com/blog/2175473 一.概述     GsonBuilder用来定制java跟json之间的转换格式   二.基本使用 实体测试类： 温馨提示：默认情况下@Expose注解是不起作用的,除非你用GsonBuilder创建Gson的时候调用了GsonBuilder.excludeField
  • 报ClassNotFoundException: Didn't find class "...Activity" on path: DexPathList gundumw100 android
    有一个工程，本来运行是正常的，我想把它移植到另一台PC上，结果报： java.lang.RuntimeException: Unable to instantiate activity ComponentInfo{com.mobovip.bgr/com.mobovip.bgr.MainActivity}: java.lang.ClassNotFoundException: Didn't f
  • JavaWeb之JSP指令 ihuning javaweb
      要点   JSP指令简介  page指令  include指令    JSP指令简介    JSP指令（directive）是为JSP引擎而设计的，它们并不直接产生任何可见输出，而只是告诉引擎如何处理JSP页面中的其余部分。 JSP指令的基本语法格式： <%@ 指令 属性名="
  • mac上编译FFmpeg跑ios 啸笑天 ffmpeg
    1、下载文件：https://github.com/libav/gas-preprocessor， 复制gas-preprocessor.pl到/usr/local/bin/下， 修改文件权限：chmod 777 /usr/local/bin/gas-preprocessor.pl 2、安装yasm-1.2.0 curl http://www.tortall.net/projects/yasm
  • sql mysql oracle中字符串连接 macroli oraclesqlmysqlSQL Server
    有的时候，我们有需要将由不同栏位获得的资料串连在一起。每一种资料库都有提供方法来达到这个目的： MySQL: CONCAT() Oracle: CONCAT(), || SQL Server: + CONCAT() 的语法如下： Mysql 中 CONCAT(字串1, 字串2, 字串3, ...): 将字串1、字串2、字串3，等字串连在一起。 请注意，Oracle的CON
  • Git fatal: unab SSL certificate problem: unable to get local issuer ce rtificate qiaolevip 学习永无止境每天进步一点点git纵观千象
    // 报错如下： $ git pull origin master fatal: unable to access 'https://git.xxx.com/': SSL certificate problem: unable to get local issuer ce rtificate   // 原因： 由于git最新版默认使用ssl安全验证，但是我们是使用的git未设
  • windows命令行设置wifi surfingll windowswifi笔记本wifi
    还没有讨厌无线wifi的无尽广告么，还在耐心等待它慢慢启动么 教你命令行设置 笔记本电脑wifi： 1、开启wifi命令 netsh wlan set hostednetwork mode=allow ssid=surf8 key=bb123456 netsh wlan start hostednetwork pause 其中pause是等待输入，可以去掉 2、
  • Linux（Ubuntu）下安装sysv-rc-conf wmlJava linuxubuntusysv-rc-conf
    安装：sudo apt-get install sysv-rc-conf 使用：sudo sysv-rc-conf 操作界面十分简洁，你可以用鼠标点击，也可以用键盘方向键定位，用空格键选择，用Ctrl+N翻下一页，用Ctrl+P翻上一页，用Q退出。     背景知识 sysv-rc-conf是一个强大的服务管理程序，群众的意见是sysv-rc-conf比chkconf
  • svn切换环境，重发布应用多了javaee标签前缀 zengshaotao javaee
    更换了开发环境，从杭州，改变到了上海。svn的地址肯定要切换的，切换之前需要将原svn自带的.svn文件信息删除，可手动删除，也可通过废弃原来的svn位置提示删除.svn时删除。   然后就是按照最新的svn地址和规范建立相关的目录信息，再将原来的纯代码信息上传到新的环境。然后再重新检出，这样每次修改后就可以看到哪些文件被修改过，这对于增量发布的规范特别有用。   检出
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他