无穷积分 ∫e^(-x^2)dx 的几种巧妙解法
目录:
- 1. 极坐标变换
- 2. 几何做法(一)
- 3. 几何做法(二)
- 4. 拉普拉斯变换
- 5. 变量代换(一)
- 6. 变量代换(二)
- 7. 构造含参变量函数
- 8. Wallis 公式
∫ − ∞ ∞ e − x 2 d x \displaystyle\int_{-\infin}^{\infin}e^{-x^2}dx ∫−∞∞e−x2dx 是一个比较常见的无穷积分,在许多领域有着重要应用。
在此介绍几种巧妙的解法,供读者欣赏。 为了您更好的阅读体验,请使用电脑浏览。
1. 极坐标变换
( ∫ − ∞ ∞ e − x 2 d x ) 2 = ∫ − ∞ ∞ e − x 2 d x ∫ − ∞ ∞ e − y 2 d y = ∫ − ∞ ∞ ∫ − ∞ ∞ e − ( x 2 + y 2 ) d x d y ( 极坐标变换 ) = ∫ 0 2 π ∫ 0 ∞ e − r 2 r d r d θ = ( ∫ 0 2 π d θ ) ( 1 2 ∫ 0 ∞ e − r 2 d r 2 ) = 2 π 1 2 = π ∴ ∫ − ∞ ∞ e − x 2 d x = π . \begin{aligned}\big(\int_{-\infin}^{\infin}e^{-x^2}dx\big)^2&=\int_{-\infin}^{\infin}e^{-x^2}dx\int_{-\infin}^{\infin}e^{-y^2}dy\\&=\int_{-\infin}^{\infin}\int_{-\infin}^{\infin}e^{-(x^2+y^2)}dxdy \quad(\textbf{极坐标变换})\\&=\int_{0}^{2\pi}\int_{0}^{\infin}e^{-r^2}rdrd\theta\\&=\big(\int_{0}^{2\pi}d\theta\big)\big(\frac{1}{2}\int_{0}^{\infin}e^{-r^2}dr^2\big)\\&=2\pi\frac{1}{2}=\pi\\ \therefore \,\,\int_{-\infin}^{\infin}e^{-x^2}dx&=\sqrt{\pi}\,.\end{aligned} (∫−∞∞e−x2dx)2∴∫−∞∞e−x2dx=∫−∞∞e−x2dx∫−∞∞e−y2dy=∫−∞∞∫−∞∞e−(x2+y2)dxdy(极坐标变换)=∫02π∫0∞e−r2rdrdθ=(∫02πdθ)(21∫0∞e−r2dr2)=2π21=π=π.
2. 几何做法(一)
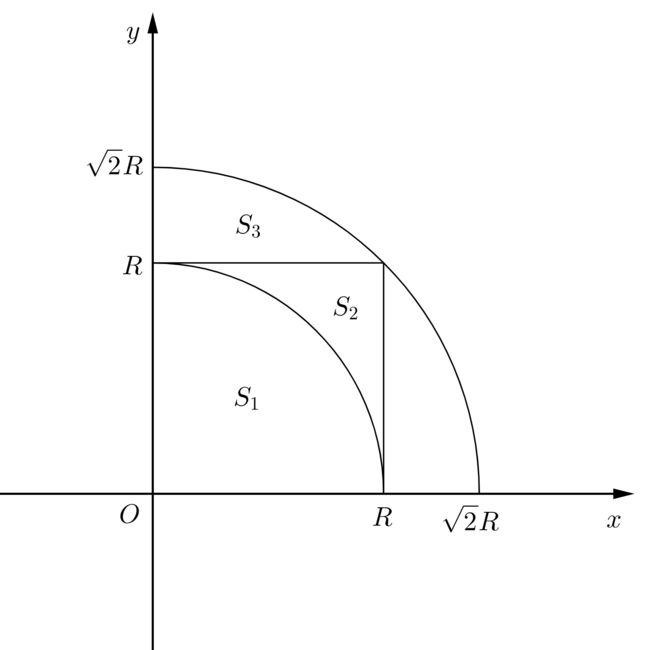
S 1 = { ( x , y ) ∣ x 2 + y 2 ≤ R 2 } S 2 = { ( x , y ) ∣ 0 ≤ x ≤ R , 0 ≤ y ≤ R } S 3 = { ( x , y ) ∣ x 2 + y 2 ≤ 2 R 2 } \begin{aligned}S_1&=\{(x,y)\,|\,x^2+y^2\leq R^2\}\\S_2&=\{(x,y)\,|\,0\leq x \leq R,\,0\leq y \leq R\}\\S_3&=\{(x,y)\,|\,x^2+y^2\leq 2R^2\}\\\,\end{aligned} S1S2S3={(x,y)∣x2+y2≤R2}={(x,y)∣0≤x≤R,0≤y≤R}={(x,y)∣x2+y2≤2R2} ( ∫ 0 R e − x 2 d x ) 2 = ∫ 0 R e − x 2 d x ∫ 0 R e − y 2 d y = ∫ 0 R ∫ 0 R e − ( x 2 + y 2 ) d x d y = ∬ S 2 e − ( x 2 + y 2 ) d x d y \begin{aligned}\big(\int_{0}^{R}e^{-x^2}dx\big)^2&=\int_{0}^{R}e^{-x^2}dx\int_{0}^{R}e^{-y^2}dy\\&=\int_{0}^{R}\int_{0}^{R}e^{-(x^2+y^2)}dxdy\\&=\iint_{S_2}e^{-(x^2+y^2)}dxdy\end{aligned} (∫0Re−x2dx)2=∫0Re−x2dx∫0Re−y2dy=∫0R∫0Re−(x2+y2)dxdy=∬S2e−(x2+y2)dxdy
∵ e − ( x 2 + y 2 ) ≥ 0 ∴ ∬ S 1 e − ( x 2 + y 2 ) d x d y ≤ ∬ S 2 e − ( x 2 + y 2 ) d x d y ≤ ∬ S 3 e − ( x 2 + y 2 ) d x d y \begin{aligned}&\because e^{-(x^2+y^2)}\geq 0 \\ &\therefore \iint_{S_1}e^{-(x^2+y^2)}dxdy\leq\iint_{S_2}e^{-(x^2+y^2)}dxdy\leq\iint_{S_3}e^{-(x^2+y^2)}dxdy\end{aligned} ∵e−(x2+y2)≥0∴∬S1e−(x2+y2)dxdy≤∬S2e−(x2+y2)dxdy≤∬S3e−(x2+y2)dxdy
∬ S 1 e − ( x 2 + y 2 ) d x d y = ∫ 0 π / 2 ∫ 0 R e − r 2 r d r d θ = ( ∫ 0 π / 2 d θ ) ( 1 2 ∫ 0 R e − r 2 d r 2 ) = π 4 ( 1 − e − R 2 ) \begin{aligned}\iint_{S_1}e^{-(x^2+y^2)}dxdy&=\int_{0}^{\pi/2}\int_{0}^{R}e^{-r^2}rdrd\theta\\&=\big(\int_{0}^{\pi/2}d\theta\big)\big(\frac{1}{2}\int_{0}^{R}e^{-r^2}dr^2\big)\\&=\frac{\pi}{4}(1-e^{-R^2})\end{aligned} ∬S1e−(x2+y2)dxdy=∫0π/2∫0Re−r2rdrdθ=(∫0π/2dθ)(21∫0Re−r2dr2)=4π(1−e−R2)
同理 ∬ S 3 e − ( x 2 + y 2 ) d x d y = π 4 ( 1 − e − 2 R 2 ) . 则 π 4 ( 1 − e − R 2 ) ≤ ∬ S 2 e − ( x 2 + y 2 ) d x d y ≤ π 4 ( 1 − e − 2 R 2 ) . 两边取极限 R → ∞ ,则 ( ∫ 0 ∞ e − x 2 d x ) 2 = ∬ R 2 e − ( x 2 + y 2 ) d x d y = π 4 . 所以 ∫ 0 ∞ e − x 2 d x = π 2 . \begin{aligned}\\&\textbf{同理}\,\iint_{S_3}e^{-(x^2+y^2)}dxdy=\frac{\pi}{4}(1-e^{-2R^2})\,.\\&\textbf{则}\,\, \frac{\pi}{4}(1-e^{-R^2})\leq\iint_{S_2}e^{-(x^2+y^2)}dxdy\leq\frac{\pi}{4}(1-e^{-2R^2})\,.\\&\textbf{两边取极限}\,R\to\infin\textbf{,则}\,\Big(\int_{0}^{\infin}e^{-x^2}dx\Big)^2=\iint_{R^2}e^{-(x^2+y^2)}dxdy=\frac{\pi}{4}.\\&\textbf{所以}\,\int_{0}^{\infin}e^{-x^2}dx=\frac{\sqrt{\pi}}{2} \,.\end{aligned} 同理∬S3e−(x2+y2)dxdy=4π(1−e−2R2).则4π(1−e−R2)≤∬S2e−(x2+y2)dxdy≤4π(1−e−2R2).两边取极限R→∞,则(∫0∞e−x2dx)2=∬R2e−(x2+y2)dxdy=4π.所以∫0∞e−x2dx=2π.
3. 几何做法(二)
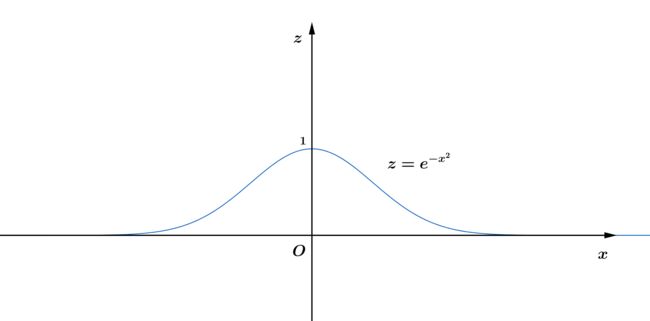
考虑曲线 z = e − x 2 绕 z 轴旋转一周生成的旋转体的体积,由高数知识 \begin{aligned}\textbf{考虑曲线}\, z=e^{-x^2}\, \textbf{绕}\, z\, \textbf{轴旋转一周生成的旋转体的体积,由高数知识}\end{aligned} 考虑曲线z=e−x2绕z轴旋转一周生成的旋转体的体积,由高数知识
V = ∫ 0 1 π x 2 d z = π ∫ 0 1 ( − ln z ) d z = π ( z − z ln z ) ∣ 0 1 = π ( 1 − lim z → 0 + ( z − z ln z ) ) = π \begin{aligned}V&= \int_0^{1}\pi x^2dz\\&=\pi \int_0^{1}(-\ln z)dz\\&=\pi (z-z\ln z)\,\Big|_0^1\\&=\pi (1-\lim_{z\to 0^{+}}(z-z\ln z))\\&=\pi\end{aligned} V=∫01πx2dz=π∫01(−lnz)dz=π(z−zlnz)∣∣∣01=π(1−z→0+lim(z−zlnz))=π
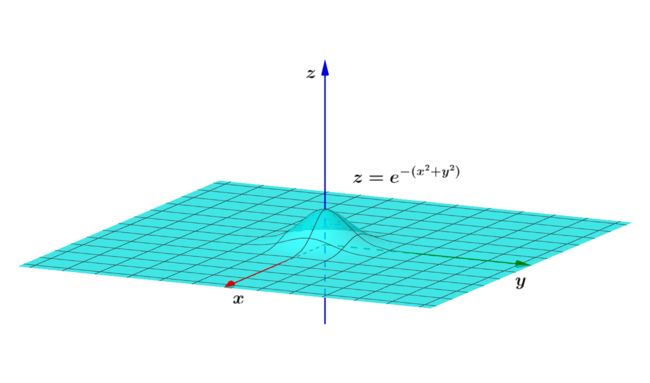
旋转体在几何上的表示如图所示,旋转生成的曲面方程为 z = e − ( x 2 + y 2 ) . 旋转体的体积也可以理解为曲面 z = e − ( x 2 + y 2 ) 与 x O y 之间部分的体积,即 \begin{aligned}&\textbf{旋转体在几何上的表示如图所示,旋转生成的曲面方程为} \,z=e^{-(x^2+y^2)}. \\ &\textbf{旋转体的体积也可以理解为曲面} \,z=e^{-(x^2+y^2)} \textbf{与}\,xOy\,\textbf{之间部分的体积,即}\end{aligned} 旋转体在几何上的表示如图所示,旋转生成的曲面方程为z=e−(x2+y2).旋转体的体积也可以理解为曲面z=e−(x2+y2)与xOy之间部分的体积,即
π = V = ∬ R 2 e − ( x 2 + y 2 ) d x d y = ∫ − ∞ ∞ e − x 2 d x ∫ − ∞ ∞ e − y 2 d y = ( ∫ − ∞ ∞ e − x 2 d x ) 2 \pi=V=\iint_{R^2}e^{-(x^2+y^2)}dxdy=\int_{-\infin}^{\infin}e^{-x^2}dx\int_{-\infin}^{\infin}e^{-y^2}dy=\big(\int_{-\infin}^{\infin}e^{-x^2}dx\big)^2 π=V=∬R2e−(x2+y2)dxdy=∫−∞∞e−x2dx∫−∞∞e−y2dy=(∫−∞∞e−x2dx)2 则 ∫ − ∞ ∞ e − x 2 d x = π . \begin{aligned} \textbf{则} \int_{-\infin}^{\infin}e^{-x^2}dx=\sqrt{\pi}.\end{aligned} 则∫−∞∞e−x2dx=π.
4. 拉普拉斯变换
令 f ( t ) = ∫ 0 ∞ e − x 2 t d x ,对 f ( t ) 作拉普拉斯变换,令 \begin{aligned}&\textbf{令}\,f(t)=\int_0^{\infin}e^{-x^2t}dx\textbf{,对}\,f(t)\,\textbf{作拉普拉斯变换,令}\end{aligned} 令f(t)=∫0∞e−x2tdx,对f(t)作拉普拉斯变换,令
F ( s ) = L [ f ( t ) ] = ∫ 0 ∞ L [ e − x 2 t ] t d x = ∫ 0 ∞ 1 s + x 2 d x = 1 s ∫ 0 ∞ 1 1 + ( x s ) 2 d ( x s ) ( let u = x s ) = 1 s arctan u ∣ 0 ∞ = π 2 s − 1 2 \begin{aligned}F(s)=\mathscr{L}[f(t)]&=\int_0^{\infin}\mathscr{L}[e^{-x^2t}]_t\,dx\\&=\int_0^{\infin}\frac{1}{s+x^2}dx\\&=\frac{1}{\sqrt{s}}\int_{0}^{\infin}\frac{1}{1+(\displaystyle \frac{x}{\sqrt{s}})^2}d(\frac{x}{\sqrt{s}}) \quad (\textrm{let}\,\, u=\frac{x}{\sqrt{s}})\\&=\frac{1}{\sqrt{s}}\arctan u\,\Big|_0^{\infin}\\&=\frac{\pi}{2}s^{-\frac{1}{2}}\end{aligned} F(s)=L[f(t)]=∫0∞L[e−x2t]tdx=∫0∞s+x21dx=s1∫0∞1+(sx)21d(sx)(letu=sx)=s1arctanu∣∣∣0∞=2πs−21
对 F ( s ) 作拉普拉斯反变换 \textbf{对}\,F(s)\,\textbf{作拉普拉斯反变换} 对F(s)作拉普拉斯反变换
f ( t ) = L − 1 [ F ( s ) ] = π 2 L − 1 [ 1 s − 1 2 + 1 ] = π 2 1 Γ ( − 1 2 + 1 ) t − 1 2 = π 2 1 Γ ( 1 2 ) t − 1 2 \begin{aligned}f(t)=\mathscr{L}^{-1}[F(s)]&=\frac{\pi}{2}\mathscr{L}^{-1}[\frac{1}{s^{-\frac{1}{2}+1}}]\\&=\frac{\pi}{2}\frac{1}{\Gamma(-\frac{1}{2}+1)}t^{-\frac{1}{2}}\\&=\frac{\pi}{2}\frac{1}{\Gamma(\frac{1}{2})}t^{-\frac{1}{2}}\end{aligned} f(t)=L−1[F(s)]=2πL−1[s−21+11]=2πΓ(−21+1)1t−21=2πΓ(21)1t−21
由余元公式: Γ ( s ) Γ ( 1 − s ) = π sin π s . 令 s = 1 2 ,则 Γ ( 1 2 ) = π , 则 f ( t ) = π 2 t , ∫ 0 ∞ e − x 2 d x = f ( 1 ) = π 2 . \begin{aligned}&\textbf{由余元公式:}\Gamma(s)\Gamma(1-s)=\frac{\pi}{\sin \pi s} .\\ &\textbf{令}\,s=\frac{1}{2}\textbf{,则}\,\,\Gamma(\frac{1}{2})=\sqrt{\pi},\\&\textbf{则}\, f(t)=\frac{\sqrt{\pi}}{2\sqrt{t}}\,,\,\int_0^{\infin}e^{-x^2}dx=f(1)=\frac{\sqrt{\pi}}{2}\,.\end{aligned} 由余元公式:Γ(s)Γ(1−s)=sinπsπ.令s=21,则Γ(21)=π,则f(t)=2tπ,∫0∞e−x2dx=f(1)=2π.
5. 变量代换(一)
令 t = x 2 ,则 d t d x = 2 x = 2 t , d x = d t 2 t . \begin{aligned}\textbf{令}\,t=x^2\textbf{,则}\,\frac{dt}{dx}=2x=2\sqrt{t} ,dx=\frac{dt}{2\sqrt{t}}\,.\end{aligned} 令t=x2,则dxdt=2x=2t,dx=2tdt.
∫ 0 ∞ e − x 2 d x = ∫ 0 ∞ e − t d t 2 t = 1 2 ∫ 0 ∞ e − t t 1 2 − 1 d t = 1 2 Γ ( 1 2 ) \int_{0}^{\infin}e^{-x^2}dx=\int_{0}^{\infin}e^{-t}\frac{dt}{2\sqrt{t}}=\frac{1}{2}\int_{0}^{\infin}e^{-t}t^{\frac{1}{2}-1}dt=\frac{1}{2}\,\Gamma(\frac{1}{2}) ∫0∞e−x2dx=∫0∞e−t2tdt=21∫0∞e−tt21−1dt=21Γ(21)
由上一种方法 Γ ( 1 2 ) = π ,则 ∫ 0 ∞ e − x 2 d x = π 2 . \begin{aligned}&\textbf{由上一种方法}\,\,\Gamma(\frac{1}{2})=\sqrt{\pi}\textbf{,则}\int_{0}^{\infin}e^{-x^2}dx=\frac{\sqrt{\pi}}{2}.\end{aligned} 由上一种方法Γ(21)=π,则∫0∞e−x2dx=2π.
6. 变量代换(二)
记 I = ∫ 0 ∞ e − x 2 d x ,令 x = u t , u > 0 为参数,则 \begin{aligned}\textbf{记}\,I=\int_0^{\infin}e^{-x^2}dx\textbf{,令}\,x=ut,\,u>0\,\textbf{为参数,则}\end{aligned} 记I=∫0∞e−x2dx,令x=ut,u>0为参数,则 I = u ∫ 0 ∞ e − u 2 t 2 d t e − u 2 I = e − u 2 u ∫ 0 ∞ e − u 2 t 2 d t \begin{aligned}I&=u\int_0^{\infin}e^{-u^2t^2}dt\\e^{-u^2}I&=e^{-u^2}u\int_0^{\infin}e^{-u^2t^2}dt\end{aligned} Ie−u2I=u∫0∞e−u2t2dt=e−u2u∫0∞e−u2t2dt 两边对变量 u 积分, I ∫ 0 ∞ e − u 2 d u = ∫ 0 ∞ ( e − u 2 u ∫ 0 ∞ e − u 2 t 2 d t ) d u \begin{aligned}\textbf{两边对变量}\,u\,\textbf{积分,} I\int_0^{\infin}e^{-u^2}du&=\int_0^{\infin}\big(e^{-u^2}u\int_0^{\infin}e^{-u^2t^2}dt\big)du\\ \end{aligned} 两边对变量u积分,I∫0∞e−u2du=∫0∞(e−u2u∫0∞e−u2t2dt)du
右边交换积分次序, \begin{aligned}\textbf{右边交换积分次序,} \end{aligned} 右边交换积分次序,
I 2 = 1 2 ∫ 0 ∞ ( ∫ 0 ∞ e − ( 1 + t 2 ) u 2 d u ) d t = 1 2 ∫ 0 ∞ 1 1 + t 2 d t = 1 2 arctan t ∣ 0 ∞ = π 4 \begin{aligned}I^2&=\frac{1}{2}\int_0^{\infin}\big(\int_0^{\infin}e^{-(1+t^2)u^2}du\big)dt\\&=\frac{1}{2}\int_0^{\infin}\frac{1}{1+t^2}dt \\&=\frac{1}{2}\arctan t\,\Big|_0^{\infin}\\&=\frac{\pi}{4}\end{aligned} I2=21∫0∞(∫0∞e−(1+t2)u2du)dt=21∫0∞1+t21dt=21arctant∣∣∣0∞=4π
所以 I = π 2 . \begin{aligned}\textbf{所以}\,I=\frac{\sqrt{\pi}}{2}\,.\end{aligned} 所以I=2π.
7. 构造含参变量函数
记 I = ∫ 0 ∞ e − x 2 d x . 令 f ( x ) = ∫ 0 1 e − x ( 1 + t 2 ) 1 + t 2 d t , x ≥ 0 ,则 \begin{aligned}\textbf{记}\,I=\int_0^{\infin}e^{-x^2}dx\,. \,\textbf{令}\,f(x)=\int_0^{1}\frac{e^{-x(1+t^2)}}{1+t^2}dt,\,x\geq 0\textbf{,则}\end{aligned} 记I=∫0∞e−x2dx.令f(x)=∫011+t2e−x(1+t2)dt,x≥0,则
f ( 0 ) = ∫ 0 1 1 1 + t 2 d t = arctan t ∣ 0 1 = π 4 f ( ∞ ) = lim x → ∞ ∫ 0 1 e − x ( 1 + t 2 ) 1 + t 2 d t = 0 \begin{aligned} &f(0)=\int_0^{1}\frac{1}{1+t^2}dt=\arctan t\,\Big|_0^1=\frac{\pi}{4} \\ &f(\infin)=\lim_{x\to\infin}\int_0^{1}\frac{e^{-x(1+t^2)}}{1+t^2}dt=0\end{aligned} f(0)=∫011+t21dt=arctant∣∣∣01=4πf(∞)=x→∞lim∫011+t2e−x(1+t2)dt=0
f ′ ( x ) = − ∫ 0 1 ∂ ∂ x ( e − x ( 1 + t 2 ) 1 + t 2 ) d t = − ∫ 0 1 e − x ( 1 + t 2 ) d t = − e − x ∫ 0 1 e − x t 2 d t ( l e t u = x t , d t = d u / x ) = − e − x x ∫ 0 x e − u 2 d u \begin{aligned}f'(x)&=-\int_0^1\frac{\partial }{\partial x}\Big(\frac{e^{-x(1+t^2)}}{1+t^2}\Big)dt\\&=-\int_0^{1}e^{-x(1+t^2)}dt \\ &=-e^{-x}\int_0^{1}e^{-xt^2}dt \quad (let\,\,u=\sqrt{x}t,\,dt=du/\sqrt{x}\,) \\&=-\frac{e^{-x}}{\sqrt{x}}\int_0^{\sqrt{x}}e^{-u^2}du\end{aligned} f′(x)=−∫01∂x∂(1+t2e−x(1+t2))dt=−∫01e−x(1+t2)dt=−e−x∫01e−xt2dt(letu=xt,dt=du/x)=−xe−x∫0xe−u2du
记 g ( x ) = ∫ 0 x e − t 2 d t , 则 f ′ ( x ) = − e − x x g ( x ) , g ′ ( x ) = e − x 2 , g ( 0 ) = 0 , g ( ∞ ) = I . \begin{aligned}&\textbf{记}\,\,g(x)=\int_0^{x}e^{-t^2}dt\,,\\&\textbf{则} \, f'(x)=-\frac{e^{-x}}{\sqrt{x}}g(\sqrt{x}),\,g'(x)=e^{-x^2},\,g(0)=0,\,g(\infin)=I.\end{aligned} 记g(x)=∫0xe−t2dt,则f′(x)=−xe−xg(x),g′(x)=e−x2,g(0)=0,g(∞)=I.
由牛顿-莱布尼兹公式, \begin{aligned}\textbf{由牛顿-莱布尼兹公式,}\end{aligned} 由牛顿-莱布尼兹公式,
f ( ∞ ) − f ( 0 ) = ∫ 0 ∞ f ′ ( x ) d x = − ∫ 0 ∞ e − x x g ( x ) d x ( let u = x , d u = d x 2 x ) = − 2 ∫ 0 ∞ e − u 2 g ( u ) d u = − 2 ∫ 0 ∞ g ( u ) g ′ ( u ) d u = − 2 ∫ 0 ∞ g ( u ) d ( g ( u ) ) = − ∫ 0 ∞ d ( g ( u ) 2 ) = g ( 0 ) 2 − g ( ∞ ) 2 \begin{aligned}f(\infin)-f(0)&=\int_0^{\infin}f'(x)dx\\&=-\int_0^{\infin}\frac{e^{-x}}{\sqrt{x}}g(\sqrt{x})dx\quad (\textrm{let} \,u=\sqrt{x},\,du=\frac{dx}{2\sqrt{x}} )\\&=-2\int_0^{\infin}e^{-u^2}g(u)du\\&=-2\int_0^{\infin}g(u)g'(u)du\\&=-2\int_0^{\infin}g(u)d(g(u))\\&=-\int_0^{\infin}d\big(g(u)^2\big)\\&=g(0)^2-g(\infin)^2 \end{aligned} f(∞)−f(0)=∫0∞f′(x)dx=−∫0∞xe−xg(x)dx(letu=x,du=2xdx)=−2∫0∞e−u2g(u)du=−2∫0∞g(u)g′(u)du=−2∫0∞g(u)d(g(u))=−∫0∞d(g(u)2)=g(0)2−g(∞)2
所以, 0 − π 4 = 0 − I 2 , I = π 2 . \begin{aligned}\textbf{所以,} 0-\frac{\pi}{4}&=0-I^2,\,I=\frac{\sqrt{\pi}}{2}\,.\end{aligned} 所以,0−4π=0−I2,I=2π.
8. Wallis 公式
Wallis 公式内容: \begin{aligned}\textbf{Wallis 公式内容:}\end{aligned} Wallis 公式内容:
lim n → ∞ ( 2 n − 1 ) ! ! ( 2 n ) ! ! 2 n = 2 π \lim_{n\to\infin}\frac{(2n-1)!!}{(2n)!!}\sqrt{2n}=\sqrt{\frac{2}{\pi}} n→∞lim(2n)!!(2n−1)!!2n=π2 推导过程参见: \textbf{推导过程参见:} 推导过程参见:Wallis公式_百度百科
∵ lim n → ∞ ( 1 + x 2 n ) n x 2 = e ∴ lim n → ∞ ( 1 + x 2 n ) − n = e − x 2 \begin{aligned}\because \,\lim_{n\to\infin} \Big(1+\frac{x^2}{n}\Big)^{\frac{n}{x^2}}&=e\\ \therefore \,\lim_{n\to\infin} \Big(1+\frac{x^2}{n}\Big)^{-n}&=e^{-x^2}\end{aligned} ∵n→∞lim(1+nx2)x2n∴n→∞lim(1+nx2)−n=e=e−x2
∫ 0 ∞ e − x 2 d x = ∫ 0 ∞ lim n → ∞ ( 1 + x 2 n ) − n d x = lim n → ∞ ∫ 0 ∞ ( 1 + x 2 n ) − n d x \begin{aligned}\int_0^{\infin}e^{-x^2}dx=&\int_0^{\infin}\lim_{n\to\infin} \Big(1+\frac{x^2}{n}\Big)^{-n}dx =\lim_{n\to\infin} \int_0^{\infin}\Big(1+\frac{x^2}{n}\Big)^{-n}dx \end{aligned} ∫0∞e−x2dx=∫0∞n→∞lim(1+nx2)−ndx=n→∞lim∫0∞(1+nx2)−ndx
( 可以验证积分与极限次序是可交换的 ) . \begin{aligned}\\&(\textbf{可以验证积分与极限次序是可交换的}).\end{aligned} (可以验证积分与极限次序是可交换的).
令 tan t = x n ,则 d t d x = 1 n ( 1 + x 2 n ) − 1 , d x = n ( 1 + x 2 n ) d t . \begin{aligned}\textbf{令}\,\tan t=\frac{x}{\sqrt{n}} \textbf{,则}\,\frac{dt}{dx}=\frac{1}{\sqrt{n}}(1+\frac{x^2}{n})^{-1},\, dx=\sqrt{n}(1+\frac{x^2}{n})dt.\end{aligned} 令tant=nx,则dxdt=n1(1+nx2)−1,dx=n(1+nx2)dt.
原式 = lim n → ∞ ∫ 0 π 2 n ( 1 + x 2 n ) − n + 1 d t = lim n → ∞ ∫ 0 π 2 n ( 1 + ( tan t ) 2 ) − ( n − 1 ) d t = lim n → ∞ n ∫ 0 π 2 ( cos t ) 2 n − 2 d t ( ∫ 0 π 2 ( cos t ) 2 n d t = ( 2 n − 1 ) ! ! ( 2 n ) ! ! π 2 ) = lim n → ∞ n ( 2 n − 3 ) ! ! ( 2 n − 2 ) ! ! π 2 = π 2 lim n → ∞ ( n − 1 ) + 1 ( 2 ( n − 1 ) − 1 ) ! ! ( 2 ( n − 1 ) ) ! ! ( let n ′ = n − 1 ) = π 2 lim n ′ → ∞ n ′ + 1 2 n ′ ( 2 n ′ − 1 ) ! ! ( 2 n ′ ) ! ! 2 n ′ = π 2 2 lim n ′ → ∞ n ′ + 1 n ′ lim n ′ → ∞ ( 2 n ′ − 1 ) ! ! ( 2 n ′ ) ! ! 2 n ′ = π 2 2 ⋅ 1 ⋅ 2 π = π 2 \begin{aligned} \textbf{原式}&=\lim_{n\to\infin} \int_0^{\frac{\pi}{2}}\sqrt{n}(1+\frac{x^2}{n})^{-n+1}dt \\&=\lim_{n\to\infin} \int_0^{\frac{\pi}{2}}\sqrt{n}(1+(\tan t)^2)^{-(n-1)}dt\\&=\lim_{n\to\infin} \sqrt{n}\int_0^{\frac{\pi}{2}}(\cos t)^{2n-2}dt \quad \Big( \int_0^{\frac{\pi}{2}}(\cos t)^{2n}dt=\frac{(2n-1)!!}{(2n)!!}\frac{\pi}{2}\,\Big)\\&=\lim_{n\to\infin} \sqrt{n}\,\frac{(2n-3)!!}{(2n-2)!!}\frac{\pi}{2} \\&=\frac{\pi}{2}\lim_{n\to\infin} \sqrt{(n-1)+1}\,\frac{(2(n-1)-1)!!}{(2(n-1))!!} \quad (\textrm{let}\,\,n'=n-1)\\&=\frac{\pi}{2}\lim_{n'\to\infin} \frac{\sqrt{n'+1}}{\sqrt{2n'}}\,\frac{(2n'-1)!!}{(2n')!!}\sqrt{2n'}\\&=\frac{\pi}{2\sqrt{2}}\lim_{n'\to\infin} \frac{\sqrt{n'+1}}{\sqrt{n'}}\lim_{n'\to\infin} \frac{(2n'-1)!!}{(2n')!!}\sqrt{2n'}\\&=\frac{\pi}{2\sqrt{2}}\cdot1\cdot\sqrt{\frac{2}{\pi}}\\&=\frac{\sqrt{\pi}}{2}\end{aligned} 原式=n→∞lim∫02πn(1+nx2)−n+1dt=n→∞lim∫02πn(1+(tant)2)−(n−1)dt=n→∞limn∫02π(cost)2n−2dt(∫02π(cost)2ndt=(2n)!!(2n−1)!!2π)=n→∞limn(2n−2)!!(2n−3)!!2π=2πn→∞lim(n−1)+1(2(n−1))!!(2(n−1)−1)!!(letn′=n−1)=2πn′→∞lim2n′n′+1(2n′)!!(2n′−1)!!2n′=22πn′→∞limn′n′+1n′→∞lim(2n′)!!(2n′−1)!!2n′=22π⋅1⋅π2=2π
所以 ∫ 0 ∞ e − x 2 d x = π 2 . \begin{aligned}\textbf{所以}\,\int_0^{\infin}e^{-x^2}dx=\frac{\sqrt{\pi}}{2}\end{aligned}. 所以∫0∞e−x2dx=2π.
若读者还有其他巧妙解法,请不吝赐教! \small \textbf{若读者还有其他巧妙解法,请不吝赐教!} 若读者还有其他巧妙解法,请不吝赐教!
文末彩蛋:大家好,这是我的孪生兄弟: \small \textbf{文末彩蛋:大家好,这是我的孪生兄弟:} 文末彩蛋:大家好,这是我的孪生兄弟: 无穷积分 ∫ sin x x d x 的几种巧妙解法! \small \textbf{无穷积分}\,\displaystyle \int \frac{\sin x}{x}dx\, \textbf{的几种巧妙解法!} 无穷积分∫xsinxdx的几种巧妙解法!
Plus: 如有错误、可以改进的地方、或任何想说的,请在评论区留言!