常见的查找与排序
今天忽然回顾了一下数据结构这块 ~ 回顾了网上大神们写的,有些内容就过来了,下次回顾方便一些 ~
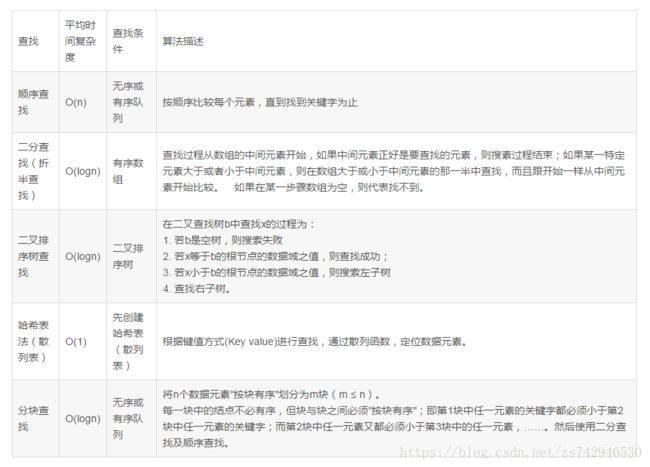
常用的查找算法主要有: 顺序查找、 二分查找
顺序查找:按数据存储的顺序进行遍历查找,对存储顺序没有要求,性能较低。
二分查找:也叫折半查找,求待查找的序列有序。每次取中间位置的值与待查关键字比较,如果中间位置的值比待查关键字大,则在前半部分循环这个查找的过程,如果中间位置的值比待查关键字小,则在后半部分循环这个查找的过程。直到查找到了为止,否则序列中没有待查的关键字
常见的排序算法有
i. 插入排序、
ii. 希尔排序、
iii.选择排序、
iv.冒泡排序、
v. 归并排序、
vi.快速排序、
vii. 堆排序、
viii. 基数排序
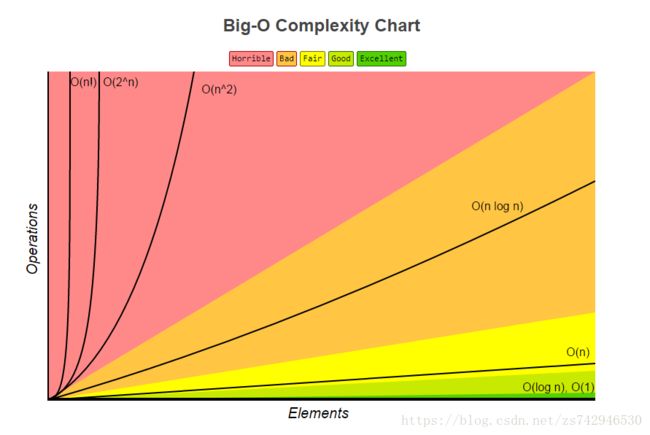
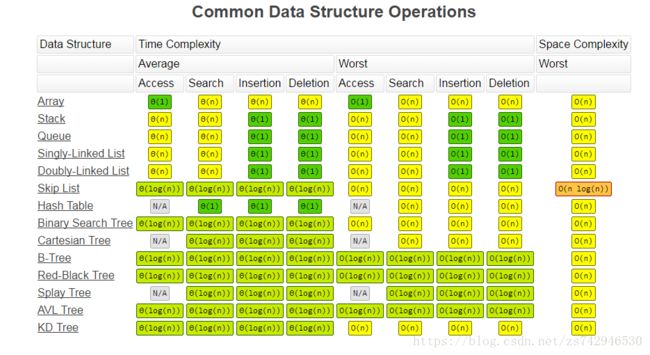
这是从大神给的网站上找到的算法的时间复杂度趋势和各个常用结构的复杂度截图。
算法的时间复杂度,用来度量算法的运行时间,记作: T(n) = O(f(n))。它表示随着 输入大小 n 的增大,算法执行需要的时间的增长速度可以用 f(n) 来描述。

二叉树的查找 O(n)
查找实现
1.顺序查找实现
public static int search(int[] arr, int v) {
for (int i=0; i <= arr.length -1; i++) {
if (v== arr[i]) {
return i + 1;
}
}
return -1;
}
2.二分查找实现
- 递归实现
public static int recurSearch(int[] arr, int v,int low, int high) {
if (low > high) {
return -1;
}
int middle = (low + high)/2;
if (arr[middle] == v) {
return middle + 1;
} else if (arr[middle] < v) {
return recurSearch(arr, v, middle + 1, high);
} else {
return recurSearch(arr, v, low, middle -1);
}
}
- 非递归实现
public static int search2(int[] arr, int v) {
int low = 0;
int high = arr.length -1;
int middle;
while (low <= high) {
middle = (low + high)/2;
if (arr[middle] == v) {
return middle + 1;
}
if (arr[middle] > v) {
high = middle -1;
} else {
low = middle + 1;
}
}
return -1;
}
测试
public static void main(String[] args) {
int[] arr= {2, 4, 6, 7, 22, 46, 73, 89, 99, 101};
System.out.println("===================非递归实现=================");
int i = search2(arr, 46);
System.out.println(i);
System.out.println(arr[i-1]);
System.out.println("===================递归实现=================");
int m = recurSearch(arr, 46, 0, arr.length-1);
System.out.println(m);
System.out.println(arr[m-1]);
System.out.println("===================顺序查找=================");
int n = search(arr, 46);
System.out.println(n);
System.out.println(arr[n-1]);
}
排序实现
1. 冒泡排序
- 原理:比较两个相邻的元素,将值大的元素交换至右端,最终形成一个从小到大的序列,需要比较比较 n-1 次即可
- 核心实现:
public static void sort(int[] array) {
for (int i = 0; i < array.length-1; i ++) {
for (int j = 0; j < array.length - i-1; j++) {
if (array[j] > array[j+1]) {
int temp = array[j];
array[j] = array[j+1];
array[j+1] = temp;
}
}
}
System.out.println("排序后的数组为:");
for (int num : array) {
System.out.print(" " + num);
}
}
2. 直接选择排序
- 原理:每一趟从待排序的记录中选出最小的元素,顺序放在已排好序的序列最后,直到全部记录排序完毕。也就是:每一趟在 n-i+1(i=1,2,…n-1)个记录中选取关键字最小的记录作为有序序列中第 i 个记录。基于此思想的算法主要有简单选择排序、树型选择排序和堆排序
- 基本思想:给定数组:int[] arr={里面 n 个数据};第 1 趟排序,在待排序数据 arr[1]~arr[n]中选出最小的数据,将它与 arrr[1]交换;第 2 趟,在待排序数据 arr[2]~arr[n]中选出最小的数据,将它与 r[2]交换;以此类推,第 i 趟在待排序数据 arr[i]~arr[n]中选出最小的数据,将它与 r[i]交换, 直到全部排序完成
- 核心实现:
public static void selectSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i ++) {
int k = i;
for(int j = k + 1; j < arr.length; j ++) {
if (arr[j] < arr[k]) {
k = j;//找出最小值的下标
}
}
//交换最小值
if (i != k) {
int temp = arr[i];
arr[i] = arr[k];
arr[k] = temp;
}
}
System.out.println("排序后的顺序:");
for (int num : arr) {
System.out.print(" " + num);
}
}
3. 直接插入排序
- 原理:利用插入法对无序数组排序时,我们其实是将数组 R 划分成两个子区间 R[1…i-1](已排好序的有序区)和 R[i…n](当前未排序的部分,可称无序区)。插入排序的基本操作是将当前无序区的第 1 个记录 R[i]插人到有序区 R[1..i-1]中适当的位置上,使 R[1…i]变为新的有序区。因为这种方法每次使有序区增加 1 个记录,通常称增量法
- 核心实现:
public static void insertSort(int[] arr) {
for (int index=1; index < arr.length; index ++) {
int temp = arr[index]; //用于比较的数据
int leftIndex = index -1;
while (leftIndex >= 0 && arr[leftIndex] > temp) {
arr[leftIndex+1] = arr[leftIndex];
leftIndex --;
}
arr[leftIndex + 1] = temp;
}
System.out.println("排序后的数组:");
for (int num : arr) {
System.out.print(" " + num);
}
}
4. 希尔排序
- 原理:希尔排序(shell sort)这个排序方法又称为缩小增量排序,是基于插入排序的优化。该方法的基本思想是:设待排序元素序列有 n 个元素,首先取一个整数 increment(小于 n)作为间隔将全部元素分为 increment 个子序列,所有距离为 increment 的元素放在同一个子序列中,在每一个子序列中分别实行直接插入排序。然后缩小间隔 increment,重复上述子序列划分和排序工作。直到最后取 increment=1,将所有元素放在同一个子序列中排序为止
- 基本思想
由于开始时,increment的取值较大,每个子序列中的元素较少,排序速度较快,到排序后期increment取值逐渐变小,子序列中元素个数逐渐增多,但由于前面工作的基础,大多数元素已经基本有序,所以排序速度仍然很快。
increment(增量)的取法:
增量increment的取法有各种方案。最初shell提出取increment=n/2向下取整,increment=increment/2向下取整,直到increment=1。但由于直到最后一步,在奇数位置的元素才会与偶数位置的元素进行比较,这样使用这个序列的效率会很低。后来Knuth提出取increment=n/3向下取整+1.还有人提出都取奇数为好,也有人提出increment互质为好。应用不同的序列会使希尔排序算法的性能有很大的差异
- 核心实现:
public static void shellSort(int[] array) {
//初始化间隔
int h = 1;
//计算最大间隔
while (h < array.length/3) {
h = h * 3 + 1;
}
while (h > 0) {
//进行插入排序
for (int index=h; index < array.length; index ++) {
int temp = array[index]; //用于比较的数据
int leftIndex = index;
while (leftIndex >= h && array[leftIndex - h] > temp) {
array[leftIndex] = array[leftIndex - h];
leftIndex -=h;
}
array[leftIndex] = temp;
}
//减小间隔
h = (h - 1)/3;
}
//打印排序后数组
System.out.println("排序后数组:");
for(int a : array) {
System.out.print(a + " ");
}
}
5. 快速排序
- 原理:基于分治的思想,是冒泡排序的改进型。首先在数组中选择一个基准点(该基准点的选取可能影响快速排序的效率),然后分别从数组的两端扫描数组,设两个指示标志(left 指向起始位置,right 指向末尾),首先从后半部分开始,如果发现有元素比该基准点的值小,就交换 left 和 right 位置的值,然后从前半部分开始扫秒,发现有元素大于基准点的值,就交换 left 和 right 位置的值,如此往复循环,直到 left>=right 然后把基准点的值放到 right 这个位置。一次排序就完成了。以后采用递归的方式分别对前半部分和后半部分排序,当前半部分和后半部分均有序时该数组就自然有序了
- 核心实现:
//第一步: 数组划分
/**
* 划分区域
* @param arr
* @param left
* @param right
* @param point
* @return
*/
public static int partition(long arr[],int left, int right,long point) {
int leftPtr = left - 1;
int rightPtr = right;
while(true) {
//做基准点左侧数据处理
while(leftPtr < rightPtr && arr[++leftPtr] < point);
//对基准点右侧处理
while(rightPtr > leftPtr && arr[--rightPtr] > point);
if(leftPtr >= rightPtr) {
break;
} else {
long tmp = arr[leftPtr];
arr[leftPtr] = arr[rightPtr];
arr[rightPtr] = tmp;
}
}
//
long tmp = arr[leftPtr];
arr[leftPtr] = arr[right];
arr[right] = tmp;
return leftPtr;
}
// 第二步: 分区排序
public static void sort(long[] arr, int left, int right) {
if(right - left <= 0) {
return;
} else {
//选择基准点
long point = arr[right];
//划分区域
int partition = partition(arr, left, right, point);
//对左侧排序
sort(arr,left,partition - 1);
//对右侧排序
sort(arr,partition + 1, right);
}
}
7. 堆排序
- 原理: 堆排序需要用到一种被称为最大堆的数据结构,与java或者lisp的gc不一样,这里的堆是一种数据结构,他可以被视为一种完全二叉树,即树里面除了最后一层其他层都是填满的。也正是因为这样,树里面每个节点的子女和双亲节点的序号都可以根据当前节点的序号直接求出
6. 归并排序
- 原理:归并排序利用的是分治的思想实现。对于给定一组数据,利用递归与分治技术将数据序列划分成为越来越小的子序列,之后对子序列排序,最后再用递归方法将排好序的子序列合并成为有序序列。合并两个子序列时,需要申请两个子序列加起来长度的内存,临时存储新的生成序列,再将新生成的序列赋值到原数组相应的位置
- 核心实现:
public static void main(String[] args) {
int[] arr = new int[10];
for(int i = 0; i < 10;i++) {
arr[i] = (int) (Math.random() * 99);
}
displayArr(arr);
mergeSort(arr, 0, arr.length - 1);
displayArr(arr);
}
public static void displayArr(int[] arr) {
System.out.print("[");
for(int num : arr) {
System.out.print(num + " ");
}
System.out.print("]");
System.out.println();
}
public static void mergeSort(int[] arr,int left,int right){
if(left7. 堆排序
堆排序需要用到一种被称为最大堆的数据结构,与java或者lisp的gc不一样,这里的堆是一种数据结构,他可以被视为一种完全二叉树,即树里面除了最后一层其他层都是填满的。也正是因为这样,树里面每个节点的子女和双亲节点的序号都可以根据当前节点的序号直接求出
8. 基数排序
- 原理: 将整数按位数切割成不同的数字,然后按每个位数分别比较
- 核心实现
public static void main(String[] args) {
int[] array = new int[10];
for(int i = 0; i < 10;i++) {
array[i] = (int) (Math.random() * 999);
}
displayArr(array);
radixSort(array); // 基数排序
displayArr(array);
}
/**
* 基数排序
*
* 参数说明:
* a -- 数组
*/
public static void radixSort(int[] a) {
int exp; // 指数。当对数组按各位进行排序时,exp=1;按十位进行排序时,exp=10;
int max = getMax(a); // 数组a中的最大值
// 从个位开始,对数组a按"指数"进行排序
for (exp = 1; max/exp > 0; exp *= 10)
countSort(a, exp);
}
/**
* 对数组按照"某个位数"进行排序(桶排序)
* 参数说明:
* a -- 数组
* exp -- 指数。对数组a按照该指数进行排序。
* 当exp=1表示按照"个位"对数组a进行排序
* 当exp=10表示按照"十位"对数组a进行排序
* 当exp=100表示按照"百位"对数组a进行排序
* ...
*/
private static void countSort(int[] a, int exp) {
int[] output = new int[a.length]; // 存储"被排序数据"的临时数组
int[] buckets = new int[10];
// 将数据出现的次数存储在buckets[]中
for (int i = 0; i < a.length; i++)
buckets[ (a[i]/exp)%10 ]++;
// 更改buckets[i]。目的是让更改后的buckets[i]的值,是该数据在output[]中的位置。
for (int i = 1; i < 10; i++)
buckets[i] += buckets[i - 1];
// 将数据存储到临时数组output[]中
for (int i = a.length - 1; i >= 0; i--) {
output[buckets[ (a[i]/exp)%10 ] - 1] = a[i];
buckets[ (a[i]/exp)%10 ]--;
}
// 将排序好的数据赋值给a[]
for (int i = 0; i < a.length; i++)
a[i] = output[i];
output = null;
buckets = null;
}
/*
* 获取数组a中最大值
* 参数说明:
* a -- 数组
*/
private static int getMax(int[] a) {
int max= a[0];
for (int i = 1; i < a.length; i++)
if (a[i] > max) max = a[i];
return max;
}
总结
排序分为 稳定排序、不稳定排序
稳定排序:排序前后两个相等的数相对位置不变,则算法稳定
冒泡排序、插入排序、归并排序和基数排序
非稳定排序:排序前后两个相等的数相对位置发生了变化,则算法不稳定
选择排序、快速排序、希尔排序、堆排序
参考: https://blog.csdn.net/zs742946530/article/details/83028119、https://blog.csdn.net/lpy1239064101/article/details/90139232