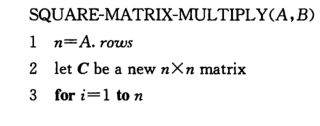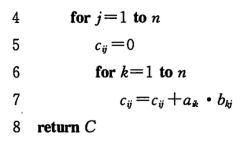图——多源最短路径
图——多源最短路径
1. 最短路径和矩阵乘法
1.1 最短路径的结构
首先，引入一个定理：对于图G=(V, E)的所有结点对最短路径问题，都满足：一条最短路径的所有子路径都是最短路径。
假定用一个 n × n n \times n n×n的邻接矩阵 W W W来表示输入图，且 W = ( w i j ) W=(w_{ij}) W=(wij)，该矩阵表示的是一个有n个结点的有向图 G = ( V , E ) G=(V, E) G=(V,E)的边的权重。其中：
w i j = { 0 若 i = j 有 向 边 ( i , j ) 的 权 重 若 i ≠ j 且 ( i , j ) ∈ E ∞ 若 i ≠ j 且 ( i , j ) ∉ E w_{ij}=\left\{ \begin{array}{lcl} 0 & & \text{若 i = j}\\ 有向边(i, j)的权重 & & \text{若 i $\neq$ j }且(i, j) \in E\\ \infty & & \text{若 i $\neq$ j }且(i, j) \notin E\end{array} \right. wij=⎩⎨⎧0有向边(i,j)的权重∞若 i = j若 i ̸= j 且(i,j)∈E若 i ̸= j 且(i,j)∈/E
另外，用 δ ( i , j ) \delta(i, j) δ(i,j) 来表示从结点 i 到结点 j 的最短路径权重。
考虑从结点 i 到结点 j 的一条最短路径 p ，假定 p 至多包含 m 条边，还假定没有权重为负值的环路，且 m 为有限值，那么有如下两种情况：
（1）如果 i = j ，则 p 的权重为0，且不包含任何边；
（2）如果 i ≠ \neq ̸= j , 则可以将路径 p 分解为两部分：从结点 i 到结点 k 的一条最短路径 p 1 p_1 p1 和结点 k 与结点 j 之间的边。其中，路径 p 1 p_1 p1 至多包含 m 条边，且 δ ( i , j ) = δ ( i , k ) + w k j \delta(i, j) = \delta(i, k) + w_{kj} δ(i,j)=δ(i,k)+wkj 。
1.2 多源最短路径的递归解
假设 l i j ( m ) l^{(m)}_{ij} lij(m) 为从结点 i 到结点 j 的至多包含 m 条边的任意路径中的最小权重。则可以分为以下两种情况：
（1）当 m = 0 时，有：
l i j ( m ) = { 0 若 i = j ∞ 若 i ≠ j l^{(m)}_{ij}=\left\{ \begin{array}{lcl} 0 & & \text{若 i = j}\\ \infty & & \text{若 i $\neq$ j }\end{array} \right. lij(m)={0∞若 i = j若 i ̸= j
（2）当 m ≥ \geq ≥ 1 ，则
l i j ( m ) = m i n 1 ≤ k ≤ n ( l i j ( m − 1 ) , l i k ( m − 1 ) + w k j ) = m i n 1 ≤ k ≤ n { l i k ( m − 1 ) + w k j } l^{(m)}_{ij} = min_{1 \leq k \leq n}( l^{(m-1)}_{ij}, l^{(m-1)}_{ik} + w_{kj}) = min_{1 \leq k \leq n}\{ l^{(m-1)}_{ik} +w_{kj}\} lij(m)=min1≤k≤n(lij(m−1),lik(m−1)+wkj)=min1≤k≤n{lik(m−1)+wkj}
因为对于所有的 j ，有 w i j w_{ij} wij = 0 ，所以上式中后面的等式成立。
注意：如果图 G 中不包含权重为负值的环路，则对于每一对结点 i 和 j ，如果 δ ( i , j ) \delta(i, j) δ(i,j) < ∞ \infty ∞，则从 i 到 j 之间存在一条最短路径。由于该最短路径是简单路径，其包含的边最多为 n-1 条。从结点 i 到结点 j 的由多于 n-1 条边构成的路径不可能有比从 i 到 j 的最短路径权重更小的权重。因此，真正的最短路径权重可由下面的公式给出：
δ ( i , j ) \delta(i, j) δ(i,j) = l i j ( n − 1 ) l_{ij}^{(n-1)} lij(n−1) = l i j ( n ) l_{ij}^{(n)} lij(n) = l i j ( n + 1 ) l_{ij}^{(n+1)} lij(n+1) = ⋯ ⋯ \cdots\cdots ⋯⋯
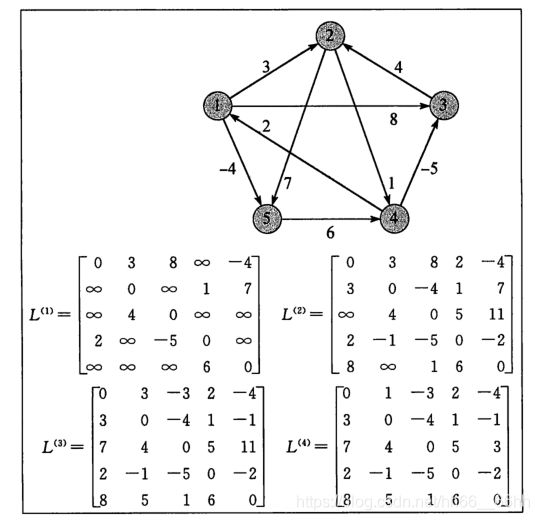
1.3 自底向上计算最短路径权重
根据输入矩阵 W = ( w i j ) W=(w_{ij}) W=(wij)，可以计算出矩阵序列 L ( 1 ) , L ( 2 ) , ⋯ , L ( n − 1 ) L^{(1)}, L^{(2)}, \cdots, L^{(n-1)} L(1),L(2),⋯,L(n−1)，最后的矩阵 L n − 1 L^{n-1} Ln−1包含的是最短路径的实际权重。另外，对于所有的结点 i 和 j ， L 1 = ( w i j ) L^{1} = (w_{ij}) L1=(wij)，即 L 1 = W L^{1} =W L1=W。
该算法的核心伪代码如下，它可以在给定 W 和 即 L m − 1 L^{m-1} Lm−1 的情况下计算出 L m L^{m} Lm ，也就是说该伪代码将最近计算出的最短路径扩展了一条边：
上述过程类似于对两个矩阵求乘积。例如计算矩阵乘积 C = A * B ，其中 A 和 B 都为 n*n 的矩阵。那么对于 i , j = 1 , 2 , ⋯ , n i, j = 1, 2, \cdots, n i,j=1,2,⋯,n ，则是计算
c i j = ∑ k = 1 n a i k ⋅ b k j c_{ij} = \sum_{k=1}^{n}a_{ik}\cdot b_{kj} cij=∑k=1naik⋅bkj
其伪代码即为：
在计算所有结点对最短路径问题的时候，可以通过对最短路径一条边一条边地扩展来计算最短路径的权重。用 A ⋅ B A \cdot B A⋅B 来表示由算法 EXTEND_SHORTEST_PATHS(A, B) 所返回的矩阵“乘积”，可以计算出下面由 n-1 个矩阵所构成的矩阵序列：
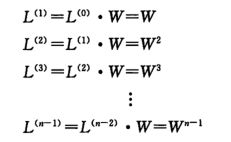
下面的伪代码程序在 O( n 4 n^4 n4) 时间内算出最终的 L n − 1 L^{n-1} Ln−1：
1.4 改进算法的运行时间
由于对所有的 m ≥ \geq ≥ n-1 ，都有 L ( m ) = L ( n − 1 ) L^{(m)} = L^{(n-1)} L(m)=L(n−1) 。因此可以仅利用 ⌈ l g ( n − 1 ) ⌉ \lceil lg(n-1) \rceil ⌈lg(n−1)⌉ 个矩阵乘积来计算$ L^{(n-1)}$ 。计算方法如下，即利用重复平方法，其复杂度为 O( n 3 l g n n^3 lgn n3lgn)：
其伪代码如下：
1.5 具体例子
1.6 代码
#include
#include
#include
#include
#include
using namespace std;
#define MAXIMUM 10000
int W[25] = {0, 3, 8, MAXIMUM, -4,
MAXIMUM, 0, MAXIMUM, 1, 7,
MAXIMUM, 4, 0, MAXIMUM, MAXIMUM,
2, MAXIMUM, -5, 0, MAXIMUM,
MAXIMUM, MAXIMUM, MAXIMUM, 6, 0};
//结点从0开始
void EXTEND_SHORTEST_PATHS(int *L, int *W, int row) {
int i, j, k, a;
int *LL = new int(row*row);
for(i=0; i