数据结构实现 9.2：并查集_树思想实现（C++版）

1. 概念及基本框架

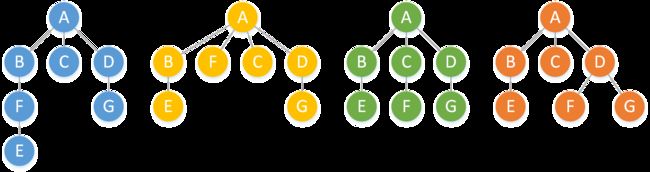
9.1 我们利用数组的结构实现了并查集，这一节我们利用树的思想来实现并查集。（但本质上还是数组，只是逻辑上的树形结构）

如上图，不同的颜色表示不同的集合，里面的字母表示元素存储的数据。下面给出并查集的基本接口。

class UnionFind{
public:
	virtual int size() = 0;
	virtual bool isEmpty() = 0;
	//是否连接
	virtual bool isConnected(int p, int q) = 0;
	//联合元素
	virtual void unionElements(int p, int q) = 0;
};

我们使用树结构来实现并查集，这里我们忽略每个元素的数据，用每个元素的阶表示元素本身，用数组中存的数字表示元素所属集合。那么并查集的实现过程如下：
1.将每个元素初始化成自身，在下面的构造函数中实现。
2.联合，将需要联合的元素中存储的数字统一为一个。
3.查找，只要数组中存储的数字是一样的，那么认为两个元素属于同一个集合。

class QuickUnion : public UnionFind{
public:
	QuickUnion(int size){
		m_data = new int[size];
		//m_num = new int[size];
		m_rank = new int[size];
		for (int i = 0; i < size; ++i){
			//每个结点指向自己
			m_data[i] = i;
			//m_num[i] = 1;
			m_rank[i] = 1;
		}
		m_size = size;
	}
	...
private:
	int *m_data;
	int m_size;
	//int *m_num;  //以i为根的树结点个数
	int *m_rank;  //结点的高度
};

m_data 用来表示数组。
m_size 表示并查集大小。
其他变量后面会详细叙述。接下来我们就对并查集的联合、查询以及一些其他基本操作用代码去实现。

2. 基本操作程序实现

2.1 联合操作

class QuickUnion : public UnionFind{
public:
	...
	//联合元素
	void unionElements(int p, int q){
		int pRoot = find(p);
		int qRoot = find(q);
		if (pRoot == qRoot){
			return;
		}
		/*
		if (m_num[pRoot] > m_num[qRoot]){
			m_data[qRoot] = pRoot;
			m_num[pRoot] += m_num[qRoot];
		}
		else{
			m_data[pRoot] = qRoot;
			m_num[qRoot] += m_num[pRoot];
		}
		*/
		if (m_rank[pRoot] > m_rank[qRoot]){
			m_data[qRoot] = pRoot;
		}
		else if (m_rank[pRoot] > m_rank[qRoot]){
			m_data[pRoot] = qRoot;
		}
		else{
			m_data[qRoot] = pRoot;
			m_rank[pRoot] = m_rank[qRoot] + 1;
		}
	}
	...
};

联合元素时，9.1 中需要遍历一遍数组，才能需要联合的元素都联合起来。如果我们利用树形结构，那么我们只需要把一棵树的根连接到需要联合的树上面，这样会大大减小时间复杂度。那么，问题在于，把谁的根连接到谁的根上面，我们可以添加一个辅助的树高度的数据，然后将树高小的树并到树高大的树上面。
注：程序中被注释掉的是依据树大小决定并的操作的，不建议这样做。连接到根节点可以实现路径压缩，实质都是为了减小树高度。

2.2 查找操作

class QuickUnion : public UnionFind{
public:
	...
	//是否连接
	bool isConnected(int p, int q){
		return find(p) == find(q);
	}
	...
private:
	int find(int index){
		if (index < 0 || index >= m_size){
			cout << "访问越界！" << endl;
			throw 0;
		}
		while (index != m_data[index]){
			m_data[index] = m_data[m_data[index]];
			index = m_data[index];
		}
		return index;
	}
	...
};

用于查找两个元素是否被联合在一起。

2.3 其他操作

并查集还有一些其他的操作，包括 并查集大小 等的查询操作。

class QuickUnion : public UnionFind{
public:
	...
	int size(){
		return m_size;
	}
	bool isEmpty(){
		return m_size == 0;
	}
	void print(){
		cout << "QuickUnion: " << "Size = " << m_size << endl;
		cout << '[';
		for (int i = 0; i < m_size; ++i){
			cout << m_data[i];
			if (i != m_size - 1){
				cout << ',';
			}
		}
		cout << ']' << endl;
	}
	...
};

3. 算法复杂度分析

3.1 联合操作

函数	最坏复杂度	平均复杂度
unionElements	O(logn)	O(logn)

因为要遍历一次数组，所以联合操作的时间复杂度为 O(logn) 。

3.2 查找操作

函数	最坏复杂度	平均复杂度
isConnected	O(1)	O(1)

总体情况：

操作	时间复杂度
并	O(logn)
查	O(1)

4. 完整代码

程序完整代码（这里使用了头文件的形式来实现类）如下：
虚函数接口 代码如下：

#ifndef __UNIONFIND_H__
#define __UNIONFIND_H__

class UnionFind{
public:
	virtual int size() = 0;
	virtual bool isEmpty() = 0;
	//是否连接
	virtual bool isConnected(int p, int q) = 0;
	//联合元素
	virtual void unionElements(int p, int q) = 0;
};

#endif

并查集 类代码：

#ifndef __QUICKFIND_H__
#define __QUICKFIND_H__

#include "UnionFind.h"

class QuickFind : public UnionFind{
public:
	QuickFind(int size){
		m_data = new int[size];
		for (int i = 0; i < size; ++i){
			m_data[i] = i;
		}
		m_size = size;
	}
	int size(){
		return m_size;
	}
	bool isEmpty(){
		return m_size == 0;
	}
	void print(){
		cout << "QuickFind: " << "Size = " << m_size << endl;
		cout << '[';
		for (int i = 0; i < m_size; ++i){
			cout << m_data[i];
			if (i != m_size - 1){
				cout << ',';
			}
		}
		cout << ']' << endl;
	}
	//是否连接
	bool isConnected(int p, int q){
		return find(p) == find(q);
	}
	//联合元素
	void unionElements(int p, int q){
		if (p == q){
			return;
		}
		for (int i = 0; i < m_size; ++i){
			if (m_data[i] == m_data[q]){
				m_data[i] = m_data[p];
			}
		}
	}
private:
	int find(int index){
		if (index < 0 || index >= m_size){
			cout << "访问越界！" << endl;
			throw 0;
		}
		return m_data[index];
	}
private:
	int *m_data;
	int m_size;
};

#endif