图像颜色空间转换—— Python 实现

介绍

在介绍颜色空间转换之前，先来介绍一下什么是颜色空间。

颜色空间指的是组织颜色的特定方式。我们知道，一种颜色可以由 红、绿、蓝 三种颜色组合出来，这里的 红、绿、蓝 三原色就是一种颜色模型。而这种由三原色组织颜色的方法就是一种颜色空间。任何一种颜色，在颜色空间中，都可以通过一个函数表示出来，在 RGB 模型中，函数的参数就是 R、G、B 三原色。

当然，同一种颜色，在不同的颜色空间中，由于侧重点不同，表现出来的色彩是不一样的。通常的图片是采用的 RGB 三原色来表示的，所以，现在，我们的目的就是将同一幅图片转换成用其他颜色空间来表示。

这篇文章中一共有四张颜色空间的转换：

• RGB -> YIQ
• RGB -> HSI
• RGB -> YCbCr
• RGB -> XYZ

颜色空间转换的算法及流程

RGB -> YIQ ：

先来介绍一下 YIQ 这个颜色空间，百度百科：

YIQ色彩空间属于NTSC系统。这里Y是指颜色的明视度，即亮度。其实Y就是图像灰度值，I和Q都指的是指色调，即描述图像色彩与饱和度的属性。YIQ颜色空间具有能将图像中的亮度分量分离提取出来的优点，并且YIQ颜色空间与RGB颜色空间之间是线性变换的关系，计算量小，聚类特性也比较好，可以适应光照强度不断变化的场合。

首先，需要将读取的 R，G，B 分量进行归一化，归一到 $[0,1]$ 区间，然后再利用下面的公式进行计算：

$$\left[\begin{array}{c}Y\\ I\\ Q\end{array}\right]=\left[\begin{array}{ccc}0.299& 0.587& 0.114\\ 0.596& -0.274& -0.322\\ 0.211& -0.523& 0.312\end{array}\right]\left[\begin{array}{c}R\\ G\\ B\end{array}\right]$$

计算完成后，需要将其标准化，即转成 $[0,255]$ 区间内。标准化的时候，要将I 和 Q 分量+128。不同的标准可能数值会有一些差异，但不会差别很大。

RGB -> HSI ：

HSI 颜色模型介绍：

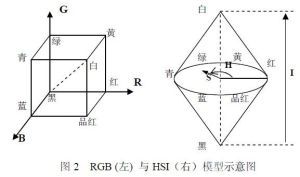
HSI〔Hue-Saturation-Intensity(Lightness),HSI或HSL〕颜色模型用H、S、I三参数描述颜色特性，其中H定义颜色的波长，称为色调；S表示颜色的深浅程度，称为饱和度；I表示强度或亮度。在HSI颜色模型的双六棱锥表示，I是强度轴，色调H的角度范围为[0，2π]，其中，纯红色的角度为0，纯绿色的角度为2π/3，纯蓝色的角度为4π/3。

RGB 转成 HSI 稍微复杂一些，具体步骤如下：

首先，需要将 R、G、B 三种颜色通道进行转换：

$$r=\frac{R}{R+G+B}g=\frac{G}{R+G+B}b=\frac{B}{R+G+B}$$

然后再进行转换，其中 H 维度需要进行一次判断，具体公式如下：

$$h={\cos }^{-1}\left(\frac{0.5\cdot \left[\left(r-g\right)+\left(r-b\right)\right]}{{\left[{\left(r-g\right)}^2+\left(r-b\right)\left(g-b\right)\right]}^{\frac{1}{2}}}\right)h\in [0,\pi ]forb\le g$$

$$h=2\pi -{\cos }^{-1}\left(\frac{0.5\cdot \left[\left(r-g\right)+\left(r-b\right)\right]}{{\left[{\left(r-g\right)}^2+\left(r-b\right)\left(g-b\right)\right]}^{\frac{1}{2}}}\right)h\in [0,\pi ]forb>g$$

$$s=1-3\cdot min(r,g,b)s\in [0,1]$$

$$i=\frac{R+G+B}{3\cdot 255}i\in [0,1]$$

计算完成后，再进行转换，转换公式如下：

$$H=\frac{h\times 180}{\pi }$$

$$S=s\times 100$$

$$I=i\times 255$$

这样就算转换成功了，计算稍微复杂一点但也不算太麻烦。最后，记得将 H 维度截断成 $[0,255]$ 区间内。

RGB -> YCbCr ：

先来看百度百科的介绍：

YCbCr或Y’CbCr有的时候会被写作：YCBCR或是Y’CBCR，是色彩空间的一种，通常会用于影片中的影像连续处理，或是数字摄影系统中。Y’为颜色的亮度(luma)成分、而CB和CR则为蓝色和红色的浓度偏移量成份。Y’和Y是不同的，而Y就是所谓的流明(luminance)，表示光的浓度且为非线性，使用伽马修正(gamma correction)编码处理。

这个转换公式比较简单，直接乘上一个转换矩阵再转换一下就可以了：

$$\left[\begin{array}{c}Y\\ Cb\\ Cr\end{array}\right]=\left[\begin{array}{c}0\\ 128\\ 128\end{array}\right]+\left[\begin{array}{ccc}0.299& 0.587& 0.114\\ -0.169& -0.331& 0.5\\ 0.5& -0.419& -0.081\end{array}\right]\left[\begin{array}{c}R\\ G\\ B\end{array}\right]$$

RGB -> XYZ ：

还是先来看看百度百科：

1931CIE-XYZ系统，就是在RGB系统的基础上，用数学方法，选用三个理想的原色来代替实际的三原色，从而将CIE-RGB系统中的光谱三刺激值和色度坐标r、g、b均变为正值。

这个跟 RGB 空间比较相似，计算也比较简单，直接乘上一个转换矩阵，转换公式如下：

$$\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]=\left[\begin{array}{ccc}0.412453& 0.357580& 0.180423\\ 0.212671& 0.715160& 0.072169\\ 0.019334& 0.119193& 0.950227\end{array}\right]\left[\begin{array}{c}R\\ G\\ B\end{array}\right]$$

实验结果

原始图片 ：

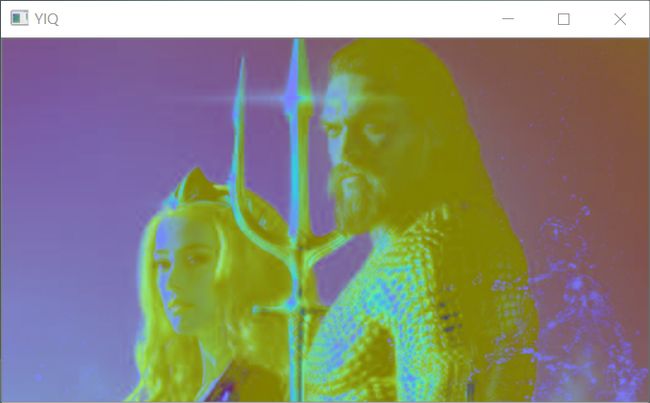
RGB -> YIQ ：

RGB -> HSI ：

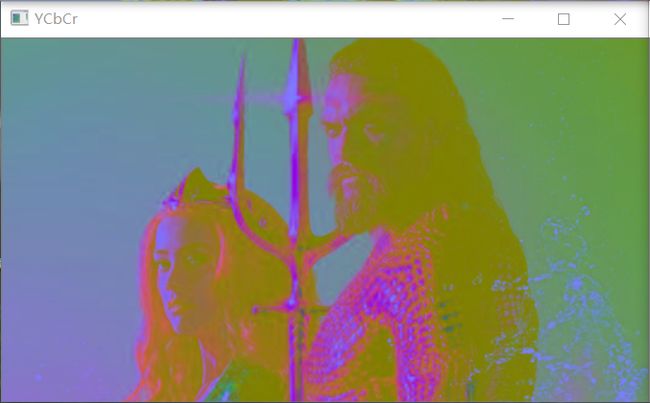
RGB -> YCbCr ：

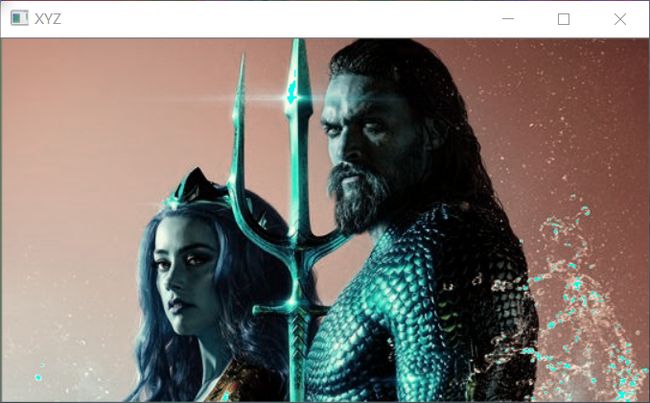
RGB -> XYZ ：

Python 代码

# -*- coding: UTF-8 -*-
import numpy as np
import math
# YIQ 变换
def imgTranYIQ(r, g, b) :
    matrix_tran = np.array([[0.299, 0.587, 0.114], \
                            [0.596, -0.274, -0.322], \
                            [0.211, -0.523, 0.312]])
    Y = []
    I = []
    Q = []
    for row in range(len(r)) :
        Y_row = []
        I_row = []
        Q_row = []
        for col in range(len(r[row])) :
            Y_row.append(matrix_tran[0][0] * r[row][col] + matrix_tran[0][1] * g[row][col] + matrix_tran[0][2] * b[row][col])
            I_row.append(matrix_tran[1][0] * r[row][col] + matrix_tran[1][1] * g[row][col] + matrix_tran[1][2] * b[row][col])
            Q_row.append(matrix_tran[2][0] * r[row][col] + matrix_tran[2][1] * g[row][col] + matrix_tran[2][2] * b[row][col])
        Y.append(Y_row)
        I.append(I_row)
        Q.append(Q_row)
    # 标准化
    return Y, I, Q

# HSI 变换
def imgTranHSI(R, G, B) :
    # 变化后的 g, b, r
    g = []
    b = []
    r = []
    for row in range(len(R)) :
        r_row = []
        g_row = []
        b_row = []
        for col in range(len(R[row])) :
            g_value = G[row][col]
            b_value = B[row][col]
            r_value = R[row][col]
            rgb_sum = g_value + b_value + r_value
            if rgb_sum == 0 :
                b_row.append(0)
                g_row.append(0)
                r_row.append(0)
            else :
                b_row.append(b_value / rgb_sum)
                g_row.append(g_value / rgb_sum)
                r_row.append(r_value / rgb_sum)
        b.append(b_row)
        g.append(g_row)
        r.append(r_row)
    # 计算 H、S、I三维通道
    H = []
    S = []
    I = []
    for row in range(len(r)) :
        H_row = []
        S_row = []
        I_row = []
        for col in range(len(r[row])) :
            r_value = r[row][col]
            g_value = g[row][col]
            b_value = b[row][col]
            # 计算 H_row_value
            sqrt_value = (r_value - g_value) * (r_value - g_value) + (r_value - b_value) * (g_value - b_value)
            sqrt_value = math.sqrt(sqrt_value)
            son_value = 0.5 * (r_value - g_value + r_value - b_value)
            if sqrt_value == 0 :
                H_row_value = 0
            else :
                acos_value = son_value / sqrt_value
                if acos_value > 1 :
                    acos_value = 1
                elif acos_value < -1 :
                    acos_value = -1
                H_row_value = math.acos(acos_value)
            if b[row][col] <= g[row][col] :
                H_row.append(H_row_value)
            else :
                H_row.append(math.pi * 2 - H_row_value)
            # 存储 S_row、I_row
            S_row.append(1 - 3 * min(r_value, g_value, b_value))
            I_row.append((R[row][col] + G[row][col] + B[row][col]) / (3 * 255))
        H.append(H_row)
        S.append(S_row)
        I.append(I_row)
    return H, S, I

# YCbCr 变换
def imgTranYCbCr(R, G, B) :
    matrix_tran = np.array([[0.299, 0.587, 0.114], \
                            [-0.169, -0.331, 0.5], \
                            [0.5, -0.419, -0.081]])
    Y = []
    Cb = []
    Cr = []
    for row in range(len(R)) :
        Y_row = []
        Cb_row = []
        Cr_row = []
        for col in range(len(R[row])) :
            Y_row.append(matrix_tran[0][0] * R[row][col] + matrix_tran[0][1] * G[row][col] + matrix_tran[0][2] * B[row][col])
            Cb_row.append(matrix_tran[1][0] * R[row][col] + matrix_tran[1][1] * G[row][col] + matrix_tran[1][2] * B[row][col] + 128)
            Cr_row.append(matrix_tran[2][0] * R[row][col] + matrix_tran[2][1] * G[row][col] + matrix_tran[2][2] * B[row][col] + 128)
        Y.append(Y_row)
        Cb.append(Cb_row)
        Cr.append(Cr_row)
    # 标准化
    return Y, Cb, Cr

# XYZ 变换
def imgTranXYZ(R, G, B) :
    matrix_tran = np.array([[0.412453, 0.357580, 0.180423], \
                            [0.212671, 0.715160, 0.072169], \
                            [0.019334, 0.119193, 0.950227]])
    X = []
    Y = []
    Z = []
    for row in range(len(R)) :
        X_row = []
        Y_row = []
        Z_row = []
        for col in range(len(R[row])) :
            X_row.append(matrix_tran[0][0] * R[row][col] + matrix_tran[0][1] * G[row][col] + matrix_tran[0][2] * B[row][col])
            Y_row.append(matrix_tran[1][0] * R[row][col] + matrix_tran[1][1] * G[row][col] + matrix_tran[1][2] * B[row][col])
            Z_row.append(matrix_tran[2][0] * R[row][col] + matrix_tran[2][1] * G[row][col] + matrix_tran[2][2] * B[row][col])
        X.append(X_row)
        Y.append(Y_row)
        Z.append(Z_row)
    return X, Y, Z

调用代码：
需要注意的是，这里我读取的是 bmp 文件，由于实验的要求，读取文件是我自己写的。其实可以直接调用 opencv 的库函数 利用 imread() 来读取。

我自己写的读文件的代码在这篇博客里：Python读取并解析 bmp 文件。这里就不细说了。

# -*- coding: UTF-8 -*-
import numpy as np
import sys
from ReadBMPFile import ReadBMPFile
import cv2
import math
import colorSpaceConversion

filePath = sys.argv[1]
# 读取 BMP 文件
bmpFile = ReadBMPFile(filePath)
# R, G, B 三个通道 [0, 255]
R = bmpFile.R
G = bmpFile.G
B = bmpFile.B
# 变化后的 g, b, r  [0, 1]
g = []
b = []
r = []
for row in range(len(R)) :
    r_row = []
    g_row = []
    b_row = []
    for col in range(len(R[row])) :
        r_row.append(R[row][col] / 255)
        g_row.append(G[row][col] / 255)
        b_row.append(B[row][col] / 255)
    r.append(r_row)
    g.append(g_row)
    b.append(b_row)

# YIQ
y, i, q = colorSpaceConversion.imgTranYIQ(r, g, b)
# 标准化 B、G、R 的值
for row in range(len(y)) :
    for col in range(len(y[row])) :
        y[row][col] = np.int8(y[row][col] * 255)
        i[row][col] = np.int8(i[row][col] * 255 + 128)
        q[row][col] = np.int8(q[row][col] * 255 + 128)
y = np.array(y, dtype = np.uint8)
i = np.array(i, dtype = np.uint8)
q = np.array(q, dtype = np.uint8)
merged = cv2.merge([y, i, q]) #合并R、G、B分量 默认顺序为 B、G、R
cv2.imshow("YIQ",merged)
cv2.imwrite(filePath.split("/")[-1].split(".")[0] + "-1160300426-YIQ.bmp", merged)

# HSI
h, s, i = colorSpaceConversion.imgTranHSI(R, G, B)
# 标准化 B、G、R 的值
for row in range(len(h)) :
    for col in range(len(h[row])) :
        h[row][col] = np.int8(h[row][col] * 180 / math.pi)
        s[row][col] = np.int8(s[row][col] * 100)
        i[row][col] = np.int8(i[row][col] * 255)
h = np.array(h, dtype = np.uint8)
s = np.array(s, dtype = np.uint8)
i = np.array(i, dtype = np.uint8)
merged = cv2.merge([h, s, i]) #合并R、G、B分量 默认顺序为 B、G、R
cv2.imshow("HSI",merged)
cv2.imwrite(filePath.split("/")[-1].split(".")[0] + "-1160300426-HSI.bmp", merged)

# YCbCr
y, Cb, Cr = colorSpaceConversion.imgTranYCbCr(R, G, B)
y_arr = np.array(y, dtype = np.uint8)
Cb_arr = np.array(Cb, dtype = np.uint8)
Cr_arr = np.array(Cr, dtype = np.uint8)
merged = cv2.merge([y_arr, Cb_arr, Cr_arr]) #合并R、G、B分量 默认顺序为 B、G、R
cv2.imshow("YCbCr",merged)
cv2.imwrite(filePath.split("/")[-1].split(".")[0] + "-1160300426-YCbCr.bmp", merged)

# XYZ
x, y, z = colorSpaceConversion.imgTranXYZ(R, G, B)
x_arr = np.array(x, dtype = np.uint8)
y_arr = np.array(y, dtype = np.uint8)
z_arr = np.array(z, dtype = np.uint8)
merged = cv2.merge([x_arr, y_arr, z_arr]) #合并R、G、B分量 默认顺序为 B、G、R
cv2.imshow("XYZ",merged)
cv2.imwrite(filePath.split("/")[-1].split(".")[0] + "-1160300426-XYZ.bmp", merged)

cv2.waitKey(0)

总结

这次的实验还是挺简单的，主要纠结的地方还是颜色空间的转换矩阵和转换方式有不同的标准，没有统一，因此不知道用哪个。总体的思路还是很清晰的。

最后，附上 github 的项目地址：实验四-图像颜色空间转换