二叉堆详解
文章目录
- 预备知识:完全二叉树
- 1.堆的定义
- 2.堆的操作
- 1.Put操作:
- 创建小根堆:
- 2.Get操作:
- 操作简介:
- 3.经典例题
- 1.【基础算法】堆排序:
- 思路:
- 代码:
- 2.合并果子:
- 思路:
- 代码:
- 3.鱼塘钓鱼(fishing):
- 思路:
- 代码:
- 4.最小函数值:
- 思路:
- 代码:
- 5.POJ1456 Supermarket:
- 思路:
- 代码:
预备知识:完全二叉树
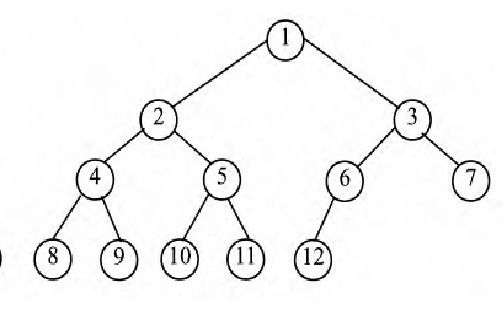
在了解堆之前,我们先了解一下完全二叉树。
完全二叉树:
一棵深度为k的二叉树,前k-1层结点都是满的,第k层的节点都集中在该层最左边的若干位置,那么这棵树就是完全二叉树。如下图
1.堆的定义
堆完全就是一棵完全二叉树。
大根堆:堆中最大元素存放在根结点中,且每一结点的子树中的结点值都小于等于该结点的值。
小根堆:堆中最小元素存放在根结点中,且每一结点的子树中的结点值都大于等于该结点的值。
2.堆的操作
1.Put操作:
Put就是往堆中加入一个元素。
创建小根堆:
1.将输入值放在堆的最后。
2.与自己的dad比较,如果dad比自己大,让自己当dad,重复第2步。否则,跳>第3步。
3.结束
代码:
void Put(int k) {
s[++size]=k;
int len=size;
while(len>1 && s[len]>1]) {
//创建大根堆就直接把s[len]>1]中的‘<’变成‘>’
swap(s[len],s[len>>1]);
len>>=1;
}
return ;
}
2.Get操作:
Get就是从堆中取出并删除一个元素。
操作简介:
1.取出堆中根结点的值。
2.把堆的最后一个结点(size)放到根的位置上,把根覆盖掉,堆长度减一。
3.把根结点置为当前父结点,即当前操作结点now。
4.如果now无儿子(now>heap_size/2),则转6;否则,把now的两(或一)个儿子中值较小的那一个置为当前子结点son。
5.比较now与son的值,如果now的值小于等于son,转6;否则交换 两个结点的值,把now指向son,转4。
6.结束。
代码:
void Get() {
printf("%d",s[1]);
s[1]=s[size--];
int now=1;
while(now*2<=size) {
int son=now*2;
if(sons[son])
swap(s[now],s[son]);
else
break;
now=son;
}
return ;
}
用Put和Get操作,堆就可以使用得溜溜熟了!
3.经典例题
1.【基础算法】堆排序:
输入N个整数,进行二叉堆排序.输出结果.
其中N≤100000
样例输入: 样例输出:
5 0 1 2 3 4
2 1 0 3 4
思路:
我们构建一个小根堆,然后Get n 次.
代码:
#include
using namespace std;
int n,a[100005],size;
void Put(int k) {
a[++size]=k;
int len=size;
while(len>1 && a[len]>1])
swap(a[len],a[len>>1]),len>>=1;
return ;
}
void Get() {
printf("%d ",a[1]);
a[1]=a[size--];
int now=1;
while(now*2<=size) {
int son=now*2;
if(sona[son]) swap(a[now],a[son]);
else break;
now=son;
}
return ;
}
int main() {
scanf("%d",&n);
for(int i=1,t;i<=n;i++)
scanf("%d",&t),Put(t);
for(int i=1;i<=n;i++) Get();
return 0;
}
2.合并果子:
一个果园里,多多已经将所有的果子打了下来,而且按果子的不同种类分成了不同的堆。
多多决定把所有的果子合成一堆。
每一次合并,多多可以把两堆果子合并到一起,消耗的体力等于两堆果子的重量之和。可
以看出,所有的果子经过n-1次合并之后,就只剩下一堆了。多多在合并果子时总共消耗
的体力等于每次合并所耗体力之和。 因为还要花大力气把这些果子搬回家,所以多多在
合并果子时要尽可能地节省体力。假定每个果子重量都为1,并且已知果子的种类数和每
种果子的数目,你的任务是设计出合并的次序方案,使多多耗费的体力最少,并输出这个
最小的体力耗费值。
例如有3种果子,数目依次为1,2,9。可以先将1、2堆合并,新堆数目为3,耗费体力为
3。接着,将新堆与原先的第三堆合并,又得到新的堆,数目为12,耗费体力为12。所以
多多总共耗费体力=3+12=15。可以证明15为最小的体力耗费值。
其中1<=n<=10000
样例输入: 样例输出:
3 15
1 2 9
思路:
我们可以发现,每一次合并都合并最小的那两个数,就可以使体力最小,那我们就使用sort?太慢了,把你T炸到天上去,我们可用堆,快多了。
代码:
#include
using namespace std;
int n,s[10005],size;
void Put(int k) {
s[++size]=k;
int len=size;
while(len>1 && s[len]>1]) {
swap(s[len],s[len>>1]);
len>>=1;
}
}
int Get() {
int now,son,ans;
ans=s[1],s[1]=s[size--];
now=1;
while(now*2<=size) {
son=now*2;
if(son 啊,这里我将Get改了一下,可以返回树根的值。
3.鱼塘钓鱼(fishing):
有N个鱼塘排成一排(N<100),每个鱼塘中有一定数量的鱼,例如:N=5时,如下表:
鱼塘编号 1 2 3 4 5
每1分钟能钓到的鱼的数量(1..1000) 10 14 20 16 9
每1分钟能钓鱼数的减少量(1..100) 2 4 6 5 3
当前鱼塘到下一个相邻鱼塘需要的时间(单位:分钟)3 5 4 4
即:在第1个鱼塘中钓鱼第1分钟内可钓到10条鱼,第2分钟内只能钓到8条鱼,……,第5分
钟以后再也钓不到鱼了。从第1个鱼塘到第2个鱼塘需要3分钟,从第2个鱼塘到第3个鱼塘需
要5分钟,……
给出一个截止时间T(T<1000),设计一个钓鱼方案,从第1个鱼塘出发,希望能钓到最多的
鱼。
假设能钓到鱼的数量仅和已钓鱼的次数有关,且每次钓鱼的时间都是整数分钟。
样例输入: 样例输出:
5 76
10 14 20 16 9
2 4 6 5 3
3 5 4 4
14
思路:
我们依次枚举一下我最多只走到1,2,3…n 鱼塘。然后创建一个大根堆,来保存现在去每个池塘的最大可钓到的鱼,每次去最大可钓到鱼的池塘钓鱼。
代码:
#include
using namespace std;
int n,m,fish[105],fj[105],t[105],size,maxx;
struct node{
int fishes,lake;
}a[105],q;
void Put(node k) {
a[++size]=k;
int len=size;
while(len>1 && a[len].fishes>a[len>>1].fishes) {
swap(a[len],a[len>>1]);
len>>=1;
}
return ;
}
void Get() {
a[1]=a[size--];
int now=1;
while(now*2<=size) {
int son=now*2;
if(sona[son].fishes)
son++;
if(a[now].fishes0 && a[1].fishes>0) {
ans+=a[1].fishes;
q.fishes=a[1].fishes-fj[a[1].lake],q.lake=a[1].lake;
Put(q);
Get();
time--;
}
if(ans>maxx) maxx=ans;
}
printf("%d",maxx);
return 0;
}
4.最小函数值:
有n(n,m≤10000)个函数,分别为F1,F2,...,Fn。定义Fi(x)=A i x 2 +Bix+Ci
(x∈N∗,正整数集合)。给定这些Ai、Bi和Ci,请求出所有函数的所有函数值中最
小的m个(如有重复的要输出多个)。
样例输入: 样例输出:
3 10 9 12 12 19 25 29 31 44 45 54
4 5 3
3 4 5
1 7 1
思路:
首先,我们可以在所有“箭头”指向1的时候,对所有箭头对应的函数值建立小根堆;然后,每次从堆顶取走那个数,并将其所对应的“箭头”指向下一个函数值,然后把这个新的函数值代替那个取走的函数值放在堆顶,并自顶向下维护堆(大家可以证明一下,一直这样操作下去,堆的性质恒成立)。
代码:
#include
using namespace std;
int n,m,k=1,a[10005],b[10005],c[10005],size;
struct node{
int biao_hao,x,z;
}s[10005],q;
void Put(node k) {
s[++size]=k;
int len=size;
while(len>1 && s[len].z>1].z) {
swap(s[len],s[len>>1]);
len>>=1;
}
}
void Get() {
s[1]=s[size--];
int now=1;
while(now*2<=size) {
int son=now*2;
if(sons[son].z)
swap(s[now],s[son]);
else
break;
now=son;
}
}
int main() {
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++) {
scanf("%d %d %d",&a[i],&b[i],&c[i]);
q.biao_hao=i,q.x=1,q.z=a[i]+b[i]+c[i];
Put(q);
}
for(int i=1;i<=m;i++) {
printf("%d ",s[1].z);
q.biao_hao=s[1].biao_hao,q.x=s[1].x+1,q.z=a[s[1].biao_hao]*q.x*q.x+b[s[1].biao_hao]*q.x+c[s[1].biao_hao];
Get();
Put(q);
}
return 0;
}
5.POJ1456 Supermarket:
一家超市出售一套产品。在截止日期dx内,它为每种产品x∈Prod赚取利润px,该截止
日期dx是从开始销售起就以时间单位的整数表示的。每种产品的销售时间正好是一个单
位。销售进度表是产品Sell≤Prod的有序子集,因此,根据Sell的顺序,每个产品
x∈Sell的销售在截止期限dx之前或dx到期时完成。销售计划的利润为Profit(Sell)
=Σx∈Sellpx。最佳销售计划是利润最高的计划。
例如,考虑产品Prod = {a,b,c,d},其中(pa,da)=(50,2),
(pb,db)=(10,1),(pc,dc)=(20 ,2)和(pd,dd)=(30,1)。
表1中列出了可能的销售时间表。例如,时间表Sell = {d,a}显示产品d的销售在时间0
开始并在时间1结束,而产品a的销售在时间1开始并在时间1开始。在时间2结束。这些产
品在截止日期之前已售出。卖出是最佳计划,其利润为80。
编写一个程序,该程序从输入文本文件读取产品集,并为每组产品计算最佳销售计划的
利润。
其中0 <= n <= 10000
样例输入:
4 50 2 10 1 20 2 30 1
7 20 1 2 1 10 3 100 2 8 2 5 20 50 10
样例输出:
80
185
思路:
我们容易想一个贪心策略:在最优解中,对于每一天,应该在保证不卖过期商品的前提下,卖利润前t大的商品。因此,我们可以依次考虑每个商品,动态维护一个满足上述性质的方案。
详细地讲,我们先把商品按过期时间排序,建立一个初始为空的小根堆,然后依次扫描商品。
1.若当前过期时间等于当前堆中的商品的个数,且当前商品的利润大于堆顶权值,则替换掉堆。
2.若当前过期时间大于当前堆中的商品的个数,直接把商品插入堆。
最后,堆中所有商品的利润之和就是答案。
代码:
#include
using namespace std;
int n,s[10005],size;
struct node{
int l,g;
}a[10005];
bool cmp(node x,node y) {
return x.g1 && s[len]>1]) {
swap(s[len],s[len>>1]);
len>>=1;
}
}
void Get() {
s[1]=s[size--];
int now=1;
while(now*2<=size) {
int son=now*2;
if(sons[son])
swap(s[now],s[son]);
else
break;
now=son;
}
}
int main() {
while(scanf("%d",&n)) {
size=0;
for(int i=1;i<=n;i++)
scanf("%d %d",&a[i].l,&a[i].g);
sort(a+1,a+n+1,cmp);//nlogn
for(int i=1;i<=n;i++) {//nlogn
if(a[i].g==size && a[i].l>s[1]) {
Put(a[i].l);
Get();
}
else if(a[i].g>size)
Put(a[i].l);
}
int ans=0;
for(int i=1;i<=size;i++)//n
ans+=s[i];
printf("%d\n",ans);
}
return 0;
}