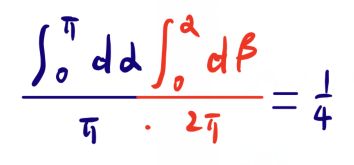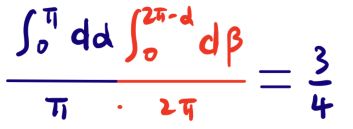概率相关实际问题汇总及解析
目录
1、圆上任意三点组成锐角三角形的概率?
2. 三个鸭子在圆形内游泳,落在同一个半圆内的概率?
3、 四个鸭子在圆形内游泳,落在同一个半圆的概率?
4、 n个骰子扔一下,点数加起来等于m的概率?
5、扔硬币,正面次数大于反面的概率?
6、抛硬币,抛多少次第一次出现连续两次正面,期望?
7、一副扑克牌54张,给3个人发牌,把大小王发到了同一个人的概率?
8、最大值的概率分布函数?
9、有n个人,m个坏人。每次检查一个人无论是不是坏人都会导致这个人死亡。那么查到第一个坏人的死掉好人的期望是多少?
10、某大公司有这么一个规定:只要有一个员工过生日,当天所有员工全部放假一天。但在其余时候,所有员工都没有假期,必须正常上班。这个公司需要雇用多少员工,才能让公司一年内所有员工的总工作时间期望值最大?
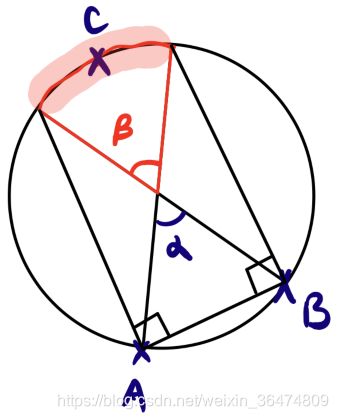
1、圆上任意三点组成锐角三角形的概率?
首先,圆上前两点A,B,与圆心的连线必然构成了一个夹角α,此夹角α是一个[0,180]度数之间的均匀分布。
如果想要构成锐角三角形,第三个点C必须落在α的对角β所对应的弧上。
α与β一样,均为[0,180]度数之间的均匀分布,所以概率是0.25
重积分的视角考虑问题
α角在0-π之间均匀分布,β在0-2π之间均匀分布,但是必须落到0-α之间才能实现构成锐角三角形。
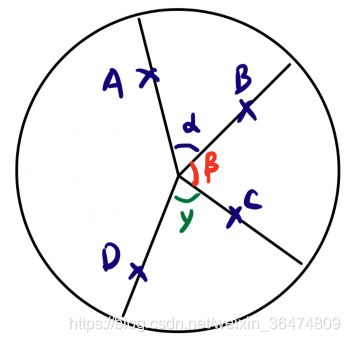
2. 三个鸭子在圆形内游泳,落在同一个半圆内的概率?
两个鸭子A,B,到圆心的夹角是0-180度均匀分布,另一个必须落到180-均匀分布的概率之外,也就是下图红色部分外,才不是同一个半圆。因此答案为0.75
重积分的视角考虑问题
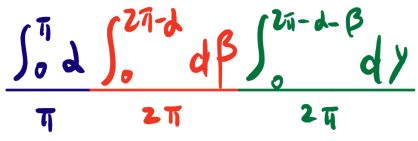
α角在0-π之间均匀分布,β在0-2π之间均匀分布,但是必须落到α的对角之外,即[0,2π-α]之间才能实现构成锐角三角形。
3、 四个鸭子在圆形内游泳,落在同一个半圆的概率?
N只鸭子的概率是 N×(2^N),4只鸭子概率是0.5
略难,重积分相对容易理解一些(暂时看不太懂,需要花时间研究下)。
4、 n个骰子扔一下,点数加起来等于m的概率?
n=m或者m=6n的时候,1/6^n
其他情况的时候分情况讨论。
第一问,掷三个骰子,掷出来的三个值之和为10的概率。可以列举出所有情况算出。
第二问,掷四个骰子,掷出来的四值之和概率最大的是哪一个。14。
5、扔硬币,正面次数大于反面的概率?
奇数次,则只有两种情况,大于或者小于,结果是0.5
偶数次,投了n次,共有2^n种情况,则为:
0.5*(总情况数-正反相等情况数)/总情况数
6、抛硬币,抛多少次第一次出现连续两次正面,期望?
概率是四分之一,期望就是4次? 抛需要两次,就是6次?
7、一副扑克牌54张,给3个人发牌,把大小王发到了同一个人的概率?
三分之一。必然发给其中一个人大王,则小王发给三个人的概率均等。所以发给这个人小王的概率是1/3
8、最大值的概率分布函数?
https://www.jianshu.com/p/0cfc3204af77
注意概念,概率密度函数与概率分布函数。
概率密度函数与概率分布函数的区别。
- max(x)=F(x)^n
- min(x)=1-(1-F(x))^n
注意F(x)是概率分布函数,不是概率密度函数
9、有n个人,m个坏人。每次检查一个人无论是不是坏人都会导致这个人死亡。那么查到第一个坏人的死掉好人的期望是多少?
把E(n,m)定义为,总数n个人,m个坏人,抽到第一个坏人之前死掉的好人的人数。
动态规划,如果抽中是坏人,则概率是m/n,死掉的好人数是0. 如果抽中好人,则概率是(n-m)/n, 期望就是死掉的好人数是 E(n-1,m)+1
10、某大公司有这么一个规定:只要有一个员工过生日,当天所有员工全部放假一天。但在其余时候,所有员工都没有假期,必须正常上班。这个公司需要雇用多少员工,才能让公司一年内所有员工的总工作时间期望值最大?
假设一年恒定365天,每个员工的生日都概率均等地分布在这365天里。
对E求导,得到n约等于365。