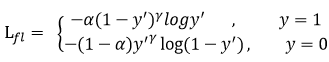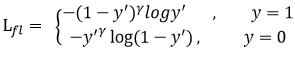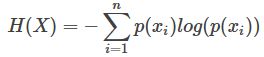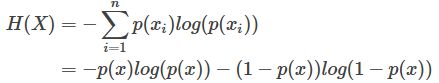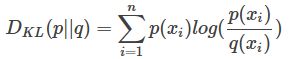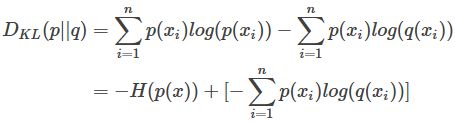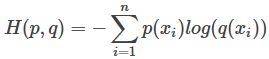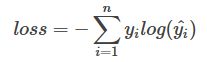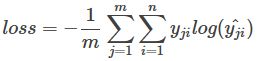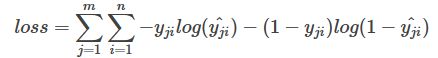机器学习算法基础问题(二)类别不均|尺寸及感受野|Batch Norm|损失函数

相关文章：

机器学习算法基础问题(一)PCA|SVM|贝叶斯|过拟合

机器学习算法基础问题(二)类别不均|尺寸及感受野|Batch Norm|损失函数

机器学习算法基础问题(三)集成学习|adaboost与XGboost| EM算法

目录

一、不均衡类别问题

1.1 问题

1.2 解决类别不均方法

重新采样

re-weight

二、featuremap尺寸与感受野尺寸

2.1 感受野的运算

2.2 featuremap尺寸

三、BN(Batch normalization)

3.1 BN可以缓解过拟合吗？

3.2 BN如何获得参数？

3.3 BN一般用在网络哪个部分？

四、损失函数

4.1 信息熵

4.1 相对熵(KL散度)

4.2 交叉熵cross entropy

4.3 单分类与多分类交叉熵

单分类交叉熵

 多分类交叉熵

代码实现

---

一、不均衡类别问题

不均衡类别问题如何解决?

1.1 问题

类别不均衡问题，比如一个类别占了99%，另一个类别占了1%。下面那些说法正确？

• 精确率和召回率不适用与衡量类别不均衡问题（正确，应该用mAP，即类的平均的准确率）
• 数据重采样可以缓解类别不均衡问题（正确，对少类别多进行采样。）
• 调整不同类别的权重，可以环节不均衡类别问题（正确，re-sample，re-weight）
• 准确度不适合衡量类别不均衡问题（准确度定义不明？）

1.2 解决类别不均方法

re-sample及re-weight

重新采样

欠采样是在多数类中进行部分采样，过采样是在少数类中重复采样。过采样和修改目标函数中正负项系数是等价的，但实际操作中效果一般不会相同。

数据增强

图像数据增强

• 镜像翻转、旋转、平移、缩放、颜色随机扰动、非线性几何变形等；
• GAN生成新样本；

文本增强

• SMOTE过采样方法
• K近邻单词替换

re-weight

• Focal Loss是个值得考虑的目标函数，原文是：Focal Loss for Dense Object Detection。
• https://www.jianshu.com/p/204d9ad9507f
• 增大小量样本的loss的权重

1.3 focal loss

focal loss是什么？

https://www.cnblogs.com/king-lps/p/9497836.html

解决one-stage目标检测中正负样本比例严重失衡的问题。该损失函数降低了大量简单负样本在训练中所占的权重，也可理解为一种困难样本挖掘。

• 解决简单样本对网络影响的比重，使得网络更加关注难样本(gama系数实现)
• 解决正负样本不均衡的问题，使得网络更加关注少量的样本(alpha系数实现)

常规交叉熵

 y'和y哪个是label ？

• y是label，
• y'是网络预测的输出。
• 对于正样本而言，输出概率越小则损失越大，负样本反之。

focal loss

 理解focal loss的物理意义之前，需要一步一步从交叉熵推及focal loss，从而理解focal loss的作用。

focal loss在交叉熵预测的概率前多了一个指数，从而使得预测的时候，gamma>0使得减少易分类样本的损失（注意gama和y不一样）。使得更关注于困难的、错分的样本。

•  网络预测为y'，在0和1之间
• 对于正样本而言，y'越小，则损失越大。
• 在损失之前，加一个系数 (1-y)^gama,，此系数作用在于降低易分样本的比重

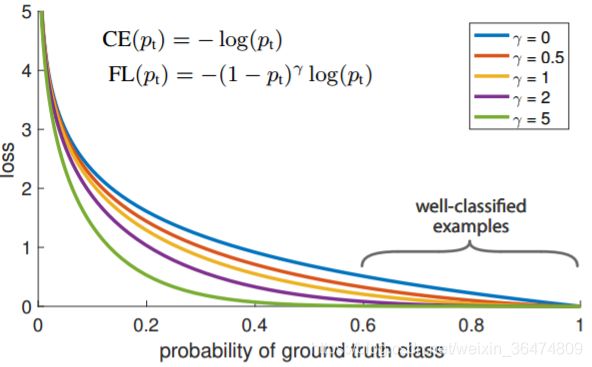
下面就来看一下系数 (1-y)^gama 是怎么起到作用的：

•  如果(1-y‘)^gama的曲线如上，(1-y‘)在0-1之间，则曲线就是上面曲线的一条
• gama值越大，则曲线值越靠下，接近1的部分就被压缩的越严重
• 这表明，如果样本越容易分离，预测概率越接近于1，则前面的系数就越小
• 通过gama函数，将易分样本的loss值比重调小，从而使得其他样本更易分。

平衡因子alpha

•  更进一步，为了解决正负样本不均衡的问题，加上系数alpha
• 少量样本前面的系数大
• 大量样本前的系数小

二、featuremap尺寸与感受野尺寸

2.1 感受野的运算

https://zhuanlan.zhihu.com/p/31004121

Receptive field (RF)

自顶层向底层的感受野运算，即从最高层开始，从上往下推导。

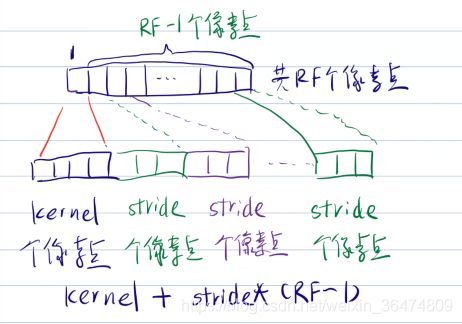
RF(n-1)=  (RF(n) - 1) * stride + kernel   

解释：下一层的感受野是上一层的感受野-1，乘上stride，再加kernel

• RF(n-1)为下一层的感受野像素点的个数，它是由上次一层的感受野的长度RF(n)推导出来
• RF中一个像素点必然是由一个卷积核大小的区域映射过来。所以下一层中需要加上kernel
• RF中除了一个像素点之外的（RF-1）个像素点，这些像素点每个都在下一层区域多感受stride个像素

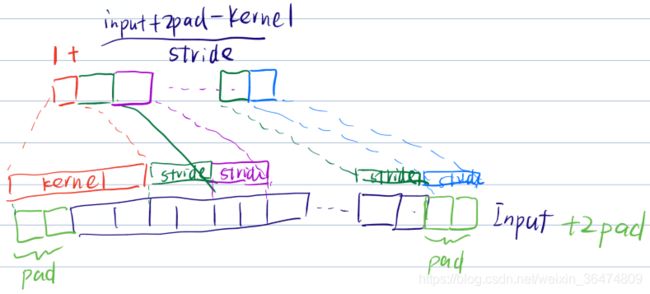
2.2 featuremap尺寸

运算公式

简化的：output=(input+2*pad-kernel)/stride)+1

带dilation较难：output=((input+2*pad-dilation*(kernel-1)+1)/stride)+1

运算结果非整数的方法

 tensorflow里面，valid系数，则运算结果向下取整，same系数则向上取整。

做题时候：卷积则向下取整，pooling则向上取整，

理解为卷积操作已经将信息通过卷积核提取了，没必要加stride重复提取，因此向下取整

pooing操作为了精简信息，已经对信息进行了精简，再向下取整损失信息过多。

三、BN(Batch normalization)

BN非常重要与基础，必须弄懂其中原理。可以详细参见下面这篇解析，BN最早的文章。

批归一化Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift论文详解

3.1 BN可以缓解过拟合吗？

可以。为什么？可以看作一种数据增强的方法。具体详细的解释可以参见原论文，How Does Batch Normalization Help Optimization?

https://arxiv.org/pdf/1805.11604.pdf

粗略讲，就是，BN输入的样本特征不仅取决于自身的样本，也取决于与之同一个batch的特征。经过了BN处理后，可以看作一个样本特征在高维空间上的拉扯，可以看作一种数据增强的过程。

这种数据增强会贯穿神经网络始终，因此BN是可以缓解过拟合。

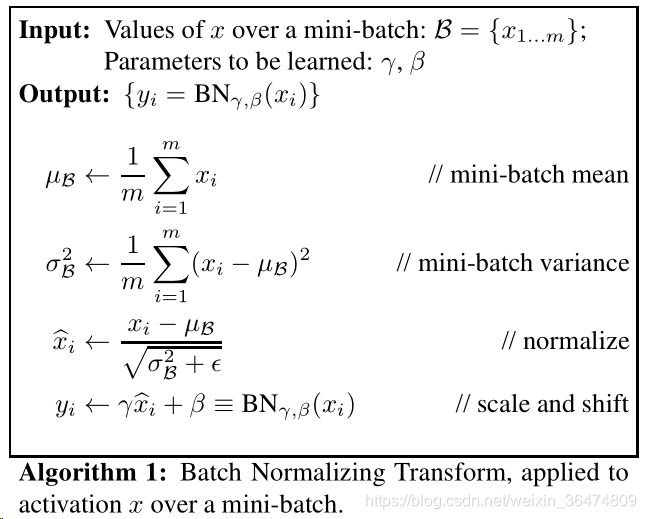
3.2 BN如何获得参数？

BN有两个参数，针对每个feature，有一个均值，和一个标准差。

BN的相应参数，是在训练过程中固定的。一旦开始测试阶段，其参数就固定下来了。

这个参数：

• 均值为均值的期望（均值的均值）
• 方差为方差的无偏估计（为什么分母要m-1，这个是概率论之中的内容 https://blog.csdn.net/qq_16587307/article/details/81328773  粗略的理解为，均值也是一个有偏的量，其中算出的均值也是有方差在里面的，所以方差m-1就要大一些）。

所以测试阶段使用的公式为：均值与标准差是从训练过程中固定下来的。

3.3 BN一般用在网络哪个部分？

激活层前还是激活层后呢？先BN，后激活。

因为我们的目的，就是为了通过BN让网络的传递更顺畅。而加入BN之后，feature更加容易被映射到激活函数的线性区，因此梯度可以更好的传递。因此，先BN，后激活。

z=g(Wu+b)是常规的激活函数，g是激活函数，z是输出。

z=g(BN(Wu+b))偏置会被归一化处理，所以加不加b经过BN之后是一样的映射，简化为下面这样：

z=g(BN(Wu))

3.4 手推一下BN的公式？

            m = K.mean(X, axis=-1, keepdims=True)#计算均值
            std = K.std(X, axis=-1, keepdims=True)#计算标准差
            X_normed = (X - m) / (std + self.epsilon)#归一化
            out = self.gamma * X_normed + self.beta#重构变换

上面四个公式含义分别为：

• 算出mini-batch的均值
• 算出mini-batch的方差
• 将层的输入通过均值方差转变为标准分布
• 将标准分布通过均值与方差线性变换为均值beta，标准差gama的分布

注意ε为常数，用于维持mini-batch的稳定

四、损失函数

https://blog.csdn.net/tsyccnh/article/details/79163834

4.1 信息熵

信息量等于概率的负对数

熵就是平均信息量，即信息量的概率加权：

比如：二项分布的信息熵，需要求和的就是p和1-p的情况：

4.1 相对熵(KL散度)

用相对熵的概念可以衡量两个分布的接近情况：

P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1]

这个反映了一个增量，即q的分布与p的分布接近的程度。即p概率分布下q的熵，与p概率分布下p的熵，相当于H(Q)-H(P) ,两个熵进行相减，就得出了KL散度。KL散度越小，则表明两者越接近。

KL散度是一种信息增量，只有当预测的Q分布完全等同于真实的P分布的时候，KL散度才为0，最小化KL散度就能够尽可能的使Q分布接近于P分布。

4.2 交叉熵cross entropy

对KL散度进行变形：

得到前部分是真实分布P的熵，后部分就是交叉熵：

 作为loss的时候，前面真实的P分布的熵可以忽略掉，直接用交叉熵作为loss。

4.3 单分类与多分类交叉熵

单分类交叉熵

单分类问题即每个样本只有一个分类数。交叉熵在单分类问题上基本是标配的方法。

y为label，y^为网络预测的概率。每个size为m，标签数量为n的batch的loss为：

 多分类交叉熵

多分类问题即标签之间的可能同时出现，因此多分类问题的交叉熵是n个二项分布的交叉熵的和。

每个n分类的batch的loss为：

n为分类数量，即交叉熵需要统计每个类上的正样本和负样本

m为mini-batch的大小

代码实现

cross_entropy=0
for i in range(batch_size)
    for n in range(n_classes)
        cross_entropy+=-label*log(predict)
print(cross_entropy)

https://blog.csdn.net/flyfish1986/article/details/79202397