本文章为原创文章,未经过允许不得转载
运行要求
运行时间限制: 2sec
内存限制: 1024MB
原题链接
题目
小明有N只猫,N为偶数。给每个猫一个编号从1到N。每个猫给一个标牌,标牌上面写着一个非负整数。小明最近在学习异或运算xor。
XOR的定义
对于N个非负整数x1,x2,x3...xN,这些数的异或 x1 xor x2 xor x3...xor xN按照下面的方式定义
x1 xor x2 xor x3 ... xor xn,把他们用2进制表示。对应的位数上的1的个数为奇数的话,那么该位的结果为1,对应的位数的1的个数为偶数的话,该位的结果为0小明在给猫的标牌上写数字的时候,赶快用一下刚刚学到的xor异或运算。
现在给1到N号猫另外一串特殊编号ai。
这里的ai表示,除了i号猫以外,其他的猫的标牌号的xor运算结果。
我们给定1到N号猫的特殊编号a1,a2,a3....aN
请根据ai求出,每个小猫的标牌号。
输入前提条件
- 所有的输入均为整数
- 2 <= N <= 200000
- N为偶数
- 0 <= ai <= 1000000000
- 给出的输入都能够找到相应的输出
输入
N
a1 a2 … aN输出
输出一行,里面包含用空格分开的N个标牌号
从左往右第i个数字代表第i只猫的标牌号
满足条件的结果由多个的话,输出任意的结果
例1
输入
4
20 11 9 24输出
26 5 7 22按照上面输出的标牌号,非自身以外的标牌号的xor结果,满足给定条件ai
- 5 xor 7 xor 22 = 20
- 26 xor 7 xor 22 = 11
- 26 xor 5 xor 22 = 9
- 26 xor 5 xor 7 = 24
读懂题目
xor 用^来代替
相当于给定一串数组a1,a2,a3,a4,a5.....aN
求另外一串数组b1,b2,b3,b4,b5.....bN
要求满足
a1 = b2 ^ b3 ^ b4 ... ^ bN
a2 = b1 ^ b3 ^ b4 ... ^ bN
a3 = b1 ^ b2 ^ b4 ... ^ bN
a4 = b1 ^ b2 ^ b3 ... ^ bN
...
aN = b1 ^ b2 ^ b3 ... ^ bN-1
想到于解xor的多元一次方程
解题思路
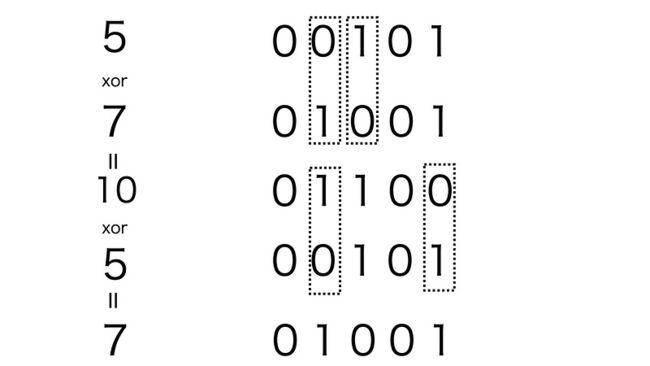
如图所示 5 ^ 7 ^ 5 = 7
在等号左边的运算中5出现了2次,7出现了1次
如图所示
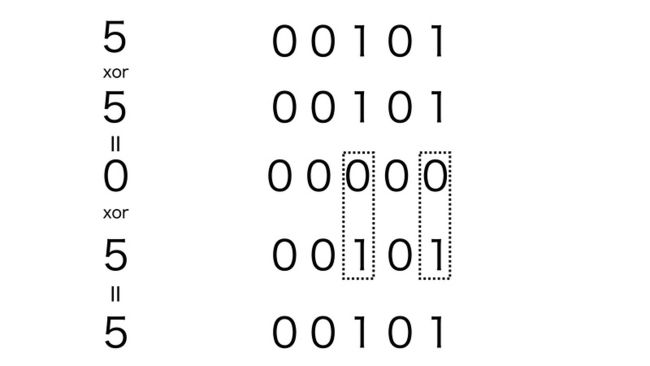
5 ^ 5 = 0
等号左边的5出现了2次,最后5被消掉
5 ^ 5 ^ 5 = 5
等号左边的5出现了3次,最后5被留下
上面两个例子就是,在异或运算中,当某一个元素最后出现的个数是偶数的时候,最后会被消掉,出现的次数是奇数的时候,最后该数字会被留下来
比如下面,最后只有m和t被留在了等号右边
m ^ m ^ m ^ n ^ n ^ t = m ^ t

如图所示,我们已知a1,a2,a3,...aN
如果我们把a1,a2,a3...aN一起做一个XOR运算的话,可以得到
a1 ^ a2 ^ a3 ... ^ aN = b1 ^ b2 ^ b3 ... ^ bN
因为N是偶数,bi都只出现了N-1次,N-1为奇数,所以最后它们bi都会被留下来
bi代表了i号猫标牌上的数字
我们这样就知道了所有的bi的xor结果
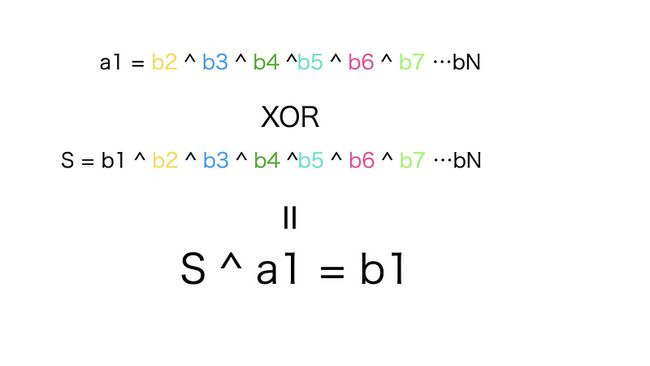
对于每个ai来说,ai ^ (b1 ^ b2 ^ b3 ^...bN) = bi
我们已知ai和(b1 ^ b2 ^ b3 ^...bN),就能求得bi
代码
N = 4
ARR = [20, 11, 9, 24]
N = int(input())
ARR = list(map(int, input().split()))
def calculate(n, arr):
s = arr[0]
for i in range(1, n):
s = s ^ arr[i]
result = []
for i in range(n):
result.append(str(arr[i] ^ s))
print(" ".join(result))
calculate(N, ARR)
总结
这一题考察了对于XOR异或运算的理解
同一个数出现的次数为偶数将会被清洗
同一个数出现的次数为偶数将会被留下
※ 另外,我会在我的微信个人订阅号上推出一些文章,欢迎关注![]()