RMQ问题--------树状数组

前言：

简述一下RMQ问题，就是区间和或者区间最值，当然有很多方法可以做这个RMQ问题，这里主要讲讲树状数组这个结构体来解决此问题。

需要弄懂的知识点：

1. tree[x]代表什么意思 ？
2. lowbit()的运算

最常解决两类问题：

No.1 区间的查询和单点的修改

No.2 区间的最大值和最小值的差值（用两个数组来存，一个存最大值，一个存最小）,也可以是求区间最大值，最小值。

树状数组浅析

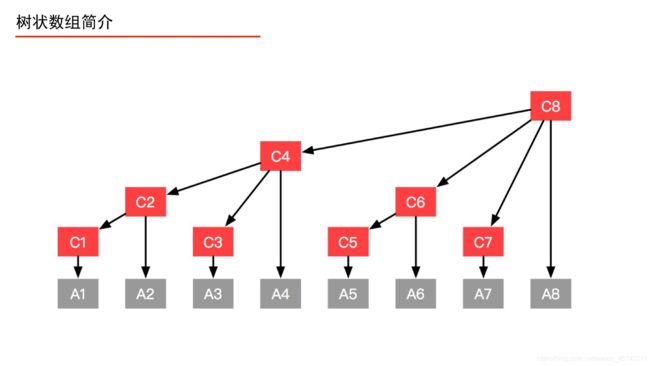
首先我们得知道，这个数据结构其实就是用数组来做的，只不过我们规范数组的用法，就成了解决问题的好帮手，上张图看看，就把此数组理解成树即可

具体说说数组的作用

NO.1
树状数组最基本的功能是加速前缀和的更新。
查询一个数组的前缀和本来是O(1)的复杂度，用树状数组则为O(logn)。
但树状数组优点在于单点更新时复杂度为O(logn)，而正常的为O(n)，这也就使得树状数组能够进行大规模的更新。
维护和查询区间和的算法中，tree[x]中储存的是[x，x-lowbit(x)+1]中每个数的和

NO.2
在求区间最值的算法中，tree[x]储存的是[x，x-lowbit(x)+1]中每个数的最大值。

lowbit运算

lowbit(n)定义为非负整数n在二进制表示下“最低为的1及其后边所有的0”构成的数值。
————摘自《算法竞赛进阶指南》
也就是lowbit(x)是x的二进制表达式中最低位的1所对应的值。
比如，6的二进制是110，所以lowbit(6)=2。

推演：
lowbit(n)的公式为：lowbit(n) = n & (~n + 1) = n & (-n)。下面事推导过程：首先将n的二进制数去反，则原来是1的位置就变成了0，原来是0的位置就变成了1。然后再将取反的数加一。我们知道，二进制数加一，则是一个“遇0变1，遇1进位”过程。那么原来的n的末尾的1以及1后面的一串0，取反变为一个0后面跟一串1时，再加一则会将这一串二进制数的1变成0，最前方的0变为1.比如：~101000 + 1 = 010111 + 1 = 011000。然后得到的数除了lowbit的那一串，其它部分都与原数n不同，所以我们再将n&得到的数，那些不同的部分就会全部变为0，而相同的部分则保持不变，这些不变的部分就是我们要求的lowbit(n)。

lowbit运算在树状数组中，是精髓，最重要的代码块
因为基础版的树状数组无非就是三个函数：
lowbit() , build_tree() , query_tree()
在后两个函数中，建树的过程中，是一直往上走的，如上面的图所示，c5到c6,再到c8，c8下一个就是c16,怎么来的呢？就是lowbit（）运算，如下：

lowbit(5) = 1; 0000 0101
5+lowbit(5)
lowbit(6) = 2; 0000 0110
6+lowbit(6)
lowbit(8) = 8; 0000 1000
8+lowbit(8)
lowbit(x)是x的二进制表达式中最低位的1所对应的值。

那么相对应的查询的时候是往下走的，就是每次迭代减去lowbit(x)，具体实现看代码

——————————————————————————————————————————————————————————

树状数组求区间和值

思路：比如[x,y]这区间的和，该怎么求？
我们先求出1到y之间的和，减去1到x之间的和，即可得到[x,y]区间和，这也是印证了树状数组最基本的功能就是加速前缀和的求法。
当我们对x迭代lowbit（）运算时，即可得到从1到x之间的和。

# include 
# include 
# include 

using namespace std;

int tree[100000],a[100000]n;

inline int lowbit(int x){
    return x&(-x);
}

int query_tree(int x){
    int sum = 0;
    while(x>=1){
        sum+=tree[x];
        x-=lowbit(x);
    }
    
    return sum;
}

void update_tree(int x,int y){  //更新点
    while(x<=n){   //往上，不超过n,为什么呢？这是我们一开始tree的定义所致
        tree[x]+=y;
        x+=lowbit(x);
    }
    return ;
}
int mian(void)
{
    cin>>n;
    srand(unsigned(time(NULL)));
    for(int i=1;i<=n;++i){
        a[i] = rand()%100+1;
        update_tree(i,a[i]);   //建立树状数组
        cout<<a[i]<<' ';
    }cout<<endl;
    
    int t;
    cin>>t;
    while(t--){
        char s[10];
        int x,y;
        cin>>s>>x>>y;
        if(s[0] == 'Q')  //查询
        {
            cout<<query_tree(y) - query_tree(x)<<endl;
        }else{    //更新点
            update_tree(x,y);
        }
    }
    return 0;
}

差分树状数组

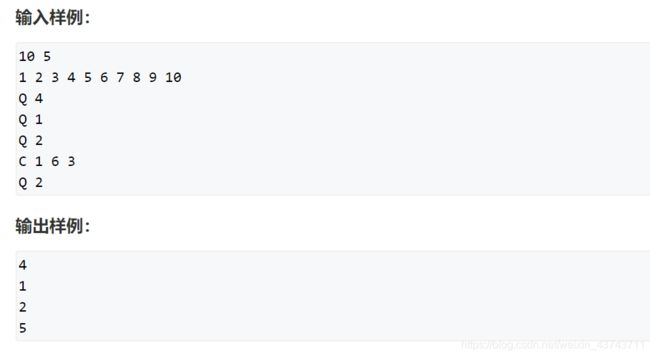
给定长度为N的数列A，然后输入M行操作指令。
第一类指令形如“C l r d”，表示把数列中第l~r个数都加d。
第二类指令形如“Q X”，表示询问数列中第x个数的值。
对于每个询问，输出一个整数表示答案。

输入格式
第一行包含两个整数N和M。
第二行包含N个整数A[i]。
接下来M行表示M条指令，每条指令的格式如题目描述所示。

输出格式
对于每个询问，输出一个整数表示答案。
每个答案占一行。
数据范围
1≤N,M≤105,
|d|≤10000,
|A[i]|≤1000000000

# include 
# include 
# include 
using namespace std;

int n,m;
const int N = 1e5+10;
int a[N],tree[N];

inline int lowbit(int& x){
    return x&(-x);
}

void add(int x,int d){
    while(x<=n){
        tree[x]+=d;
        x+=lowbit(x);
    }
    return ;
}

int query(int x){
    int ans = 0;
    while(x>0){
        ans+=tree[x];
        x-=lowbit(x);
    }
    return ans;
}
int main(void)
{
    cin>>n>>m;
    for(int i=1;i<=n;++i){
        scanf("%d",&a[i]);
        add(i,a[i]-a[i-1]);
    }
    
    while(m--){
        char s[5];
        scanf("%s",s);
        if(s[0]=='Q'){
            int l;
            cin>>l;
            cout<<query(l)<<endl;
        }
        else{
            int x,y,c;
            cin>>x>>y>>c;
            add(x,c);
            add(y+1,-c);
        }
    }
    return 0;
}

树状数组求区间最大值

（原题链接：请点击查阅！）

我们设query(x,y)，表示[x，y]区间的最大值

因为tree[y]表示的是[y,y-lowbit(y)+1]的最大值。
例如：tree[6] ----> 表示区间【5,6】的最大值。

然后，我们可以这样求解：

若y-lowbit(y) > =x ，则query(x,y) = max( tree[y] , query(x, y-lowbit(y)) );

若y-lowbit(y)

#include 
#include 
#include 
using namespace std;
 
const int MAXN = 3e5;
int a[MAXN], h[MAXN];
int n, m;
 
int lowbit(int x)
{
	return x & (-x);
}
void updata(int x)
{
	int lx, i;
	while (x <= n)
	{
		h[x] = a[x];
		lx = lowbit(x);
		for (i=1; i<lx; i<<=1)
			h[x] = max(h[x], h[x-i]);
		x += lowbit(x);
	}		
}
int query(int x, int y)
{
	int ans = 0;
	while (y >= x)
	{
		ans = max(a[y], ans);
		y --;
		for (; y-lowbit(y) >= x; y -= lowbit(y))
			ans = max(h[y], ans);
	}
	return ans;
}
int main()
{
	int i, j, x, y, ans;
	char c;
	while (scanf("%d%d",&n,&m)!=EOF)
	{
		for (i=1; i<=n; i++)
			h[i] = 0;
		for (i=1; i<=n; i++)
		{
			scanf("%d",&a[i]);
			updata(i);
		}
		for (i=1; i<=m; i++)
		{
			scanf("%c",&c);
			scanf("%c",&c);
			if (c == 'Q')
			{
				scanf("%d%d",&x,&y);
				ans = query(x, y);
				printf("%d\n",ans);
			}
			else if (c == 'U')
			{
				scanf("%d%d",&x,&y);
				a[x] = y;
				updata(x);
			}
		}
	}
	return 0;
}