关于Softmax

基本公式：
$$S_i=\frac{e^{z_i}}{{\sum }_{j=0}^C{e}^{z_j}}$$
其中，输入$z$为一个C维向量，输出$S$也是一个C维向量，这里的C通常就是分类里面的类别数量。公式的分母对于每个输出$S_i$都是一样的，区别只在于分子$e^{z_i}$，从这个角度看softmax就有点类似于归一化操作，实际效果也是把任意范围的输入变成[0,1]的输出（维度不变）。图像如下：

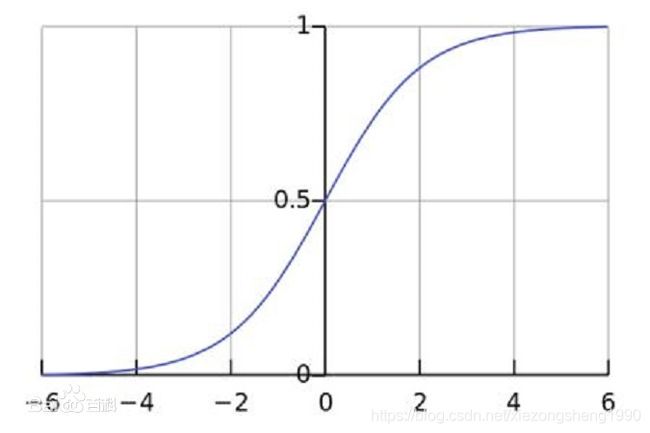
softmax交叉熵损失函数实际上就是通过softmax来计算各个类别的预测得分$\widehat{y_j}$，然后根据得分计算Loss：
$$L_{ce}=-ylog(\hat{y})=-log(\hat{y})$$
其中上式中$y$为标签值，也就是1，$\hat{y}$是根据上面公式算出来的得分（分子为正确类别y对应的特征值$z_y$)：
$$\hat{y}=\frac{e^{z_y}}{{\sum }_{j=0}^C{e}^{z_j}}$$
两式合并：
$$L_{ce}=-log(\frac{e^{z_y}}{{\sum }_{j=0}^C{e}^{z_j}})$$
参考从最优化的角度看待Softmax损失函数，这里对Softmax的更深层次的的含义进行一下探究。
在分类问题中，我们最朴素的目标就是输出一个C维向量，使目标类别（假设为第y类）$z_y$最大，形式化为（这里下标$y$和$j$表示类别编号）：
$$z_y>z_j(\forall j\ne y)$$
在优化的过程中，就是要使$z_y$变大，而其他的$z_{j\ne y}$变小，于是目标函数：
$$L=\sum _{j!=y}^C(z_j-z_y)$$
为了避免$z$无限制的下降，对其进行限制（类似于relu）
$$L=\sum _{j!=y}^{C}max(z_j-z_y,0)$$
这个函数的优化结果将使$L$逐渐下降到0，此时分类边界$z_{j\ne y}=z_y$。

但通常只有平时努力想考100分同学真正考试的时候才能拿到95分，目标是95分的同学只能考90分。于是我们人为的加入一个margin（这个margin得适中，太小了不起作用，太大了模型可能不收敛，一般类别数C较少时margin稍大，反之亦然），强迫不同的类别之间的分数拉大距离，使训练时候的难度更大，这样实际测试的时候泛化能力才更强，于是：
$$L=\sum _{j!=y}^{C}max(z_j-z_y+m,0)$$
这个目标函数中，$L$对所有的类别（j=0,1…C)都将会进行考虑，即计算梯度的时候会对所有的$z_j$进行计算，更新权重的时候梯度也会向所有类别的路径进行传播。这在二分类问题中一般没什么问题（二分类中的CE函数$L=-\frac{1}{m}{\sum }_{i=0}^m[y_{i}log\widehat{y_i}+(1-y_i)log(1-\widehat{y_i})]$，既考虑目标类别，也考虑非目标类别），但在多分类中，特别是类别数特别多的情况下，如果所有类别都进行计算，将会有大量的非目标分数得到优化，这样每次优化时的梯度可能会比较大，且偏向非目标类别，极易梯度爆炸。
所以多分类时一般只考虑目标类别和“个别”非目标类别，达到平衡的目的。而这个“个别”的非目标类别，我们应该怎么挑呢？
无疑，我们应该挑分数最大的那个（分数最大说明错的离谱，类似于hard example mining），于是我们的目标就是：
使目标分数比最大的非目标分数更大
形式化如下：
$$L=max(ma{x}_{j\ne y}(z_j)-z_y+m,0)$$
这里就没有了对所有类别的求和，而是改成了求所有类别里的最大分数值，这样目标类别和非目标类别都只求一个梯度，即优化参数时只有一个+1和一个-1梯度进入网络，达到平衡的目的。
为了兼顾各个非目标类别，可以对max函数做一个smooth：
$$ma{x}_{j\ne y}(z_j)\approx log(\sum _{j=0,j\ne y}^C{e}^{z_j})$$
上式把max smooth成LogSumExp，而其中LogSumExp的梯度刚好就是softmax：
$$\frac{\partial log({\sum }_{j=0,j\ne y}^C{e}^{z_j})}{\partial z_i}=\frac{e^{z_i}}{{\sum }_{j=0,j\ne y}^C{e}^{z_j}}$$
相当于通过softmx的分配方式，给其他非目标类别分一点梯度。
于是目标函数变成：
$$L=max(log(\sum _{j=0,j\ne y}^C{e}^{z_j})-z_y,0)$$
更进一步，还可以把$max(x,0)$smooth成softplus，即$max(x,0)\approx log(1+e^x)$，两者的图像对比如下。

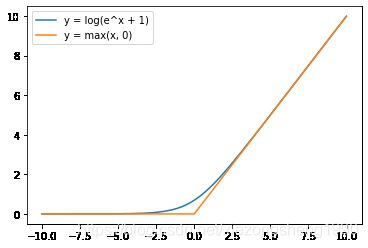
于是：
$$\begin{array}{rl}L& =log(1+e^{log({\sum }_{j=0,j\ne y}^C{e}^{z_j})-z_y})\\ & =log(1+\frac{e^{log({\sum }_{j=0,j\ne y}^C{e}^{z_j})}}{e^{z_y}})\\ & =log(\frac{{\sum }_{j=0,j\ne y}^C{e}^{z_j}+e^{z_y}}{e^{z_y}})\\ & =log(\frac{{\sum }_{j=0}^C{e}^{z_j}}{e^{z_y}})\\ & =-log(\frac{e^{z_y}}{{\sum }_{j=0}^C{e}^{z_j}})\end{array}$$
这个就是softmax交叉熵损失函数了。
从上述分析过程我们可以看到，softmax虽然看起来简单，但实际上从朴素目标函数出发，包含了平滑过程（使优化过程更加通畅）、非目标类别选择（使正负梯度得以平衡）、梯度分配（梯度按softmax方式分配给各个非目标类别）等过程。