图示理解卷积运算、逆卷积运算、Tensorflow、tf.nn.conv2d_transpose、Conv2DSlowBackpropInput: Size of out_backprop doesn

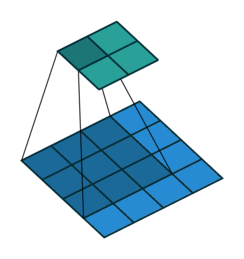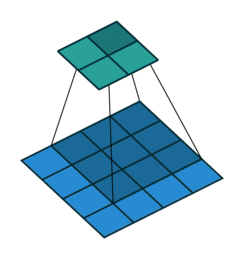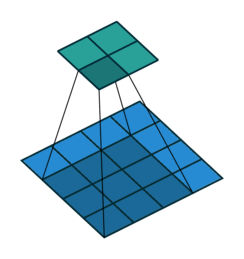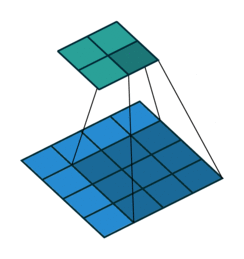
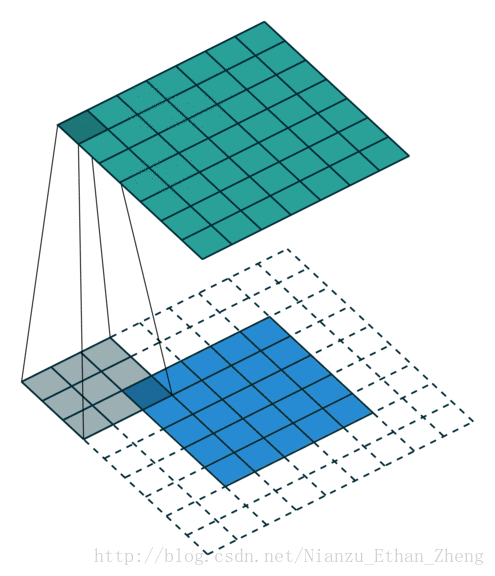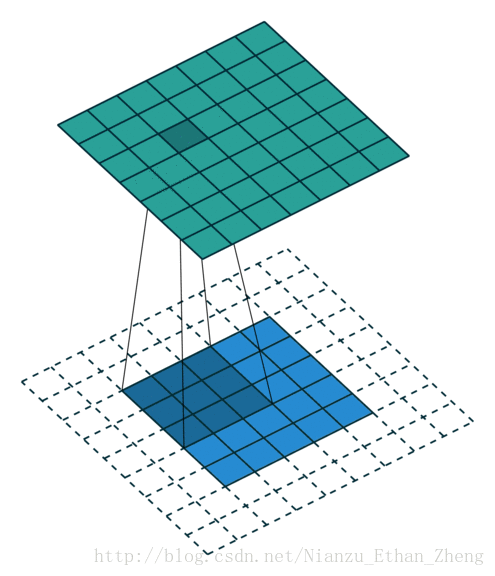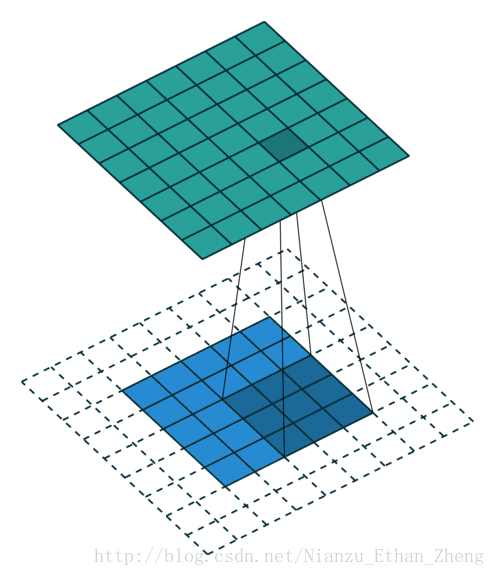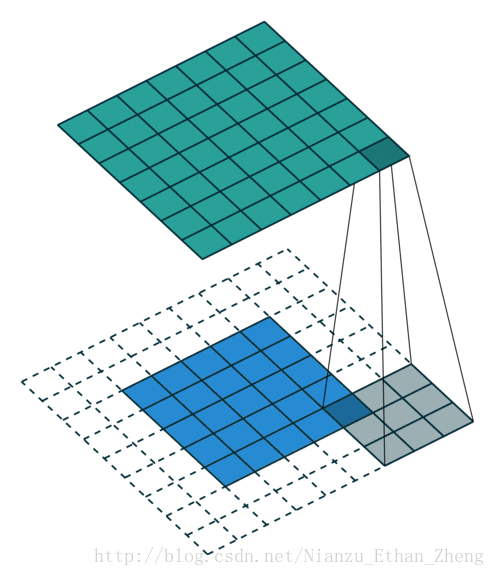
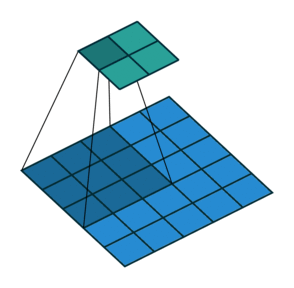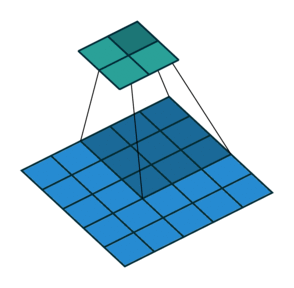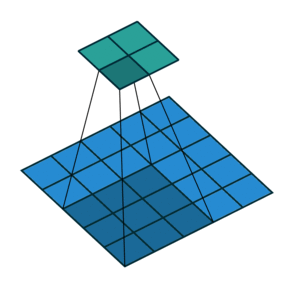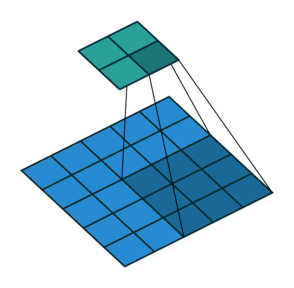
卷积运算

这里以二维卷积为例讨论：

正方形输入( i1=i2=i )

正方形卷积核大小（ k1=k2=k ）

相同的步长（ s1=s2=s ）

相同的零填充（ p1=p2=p ）

第一种情况： s=1,p=0,i=4,k=3

从输入图像的最右边开始，一个步长一个步长直到抵达图像的另外一边
输入图像的大小为：

o=(i−k)+1

第二种情况： s=1,p=2,i=5,k=3

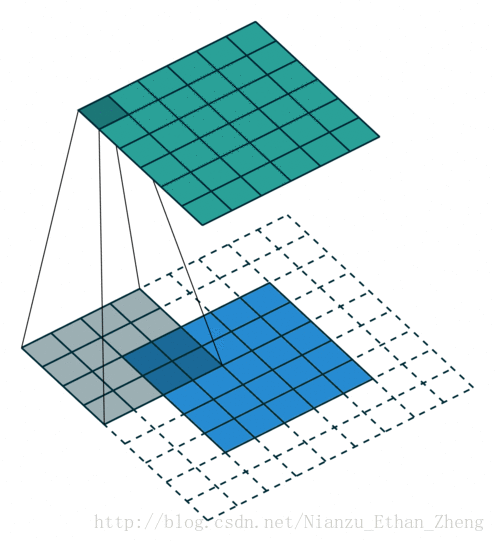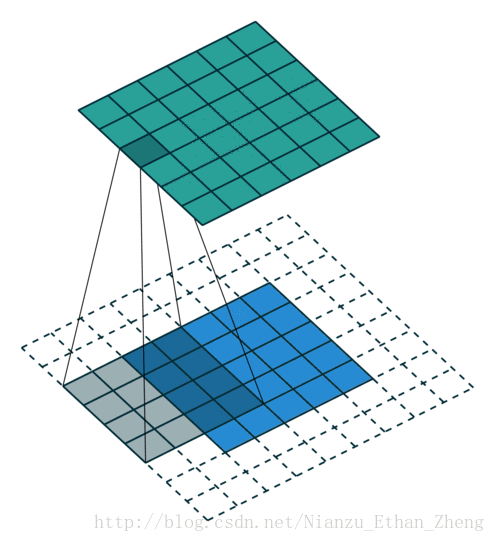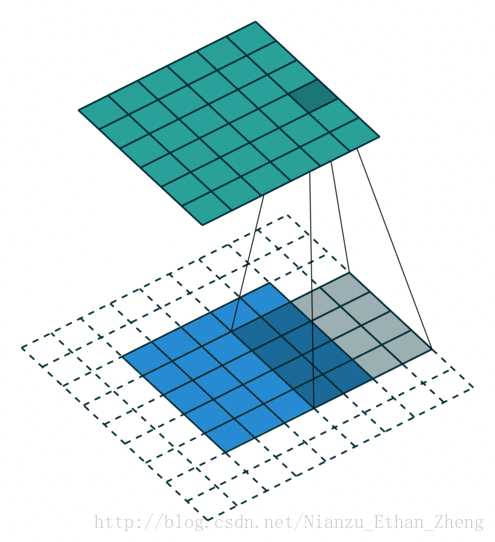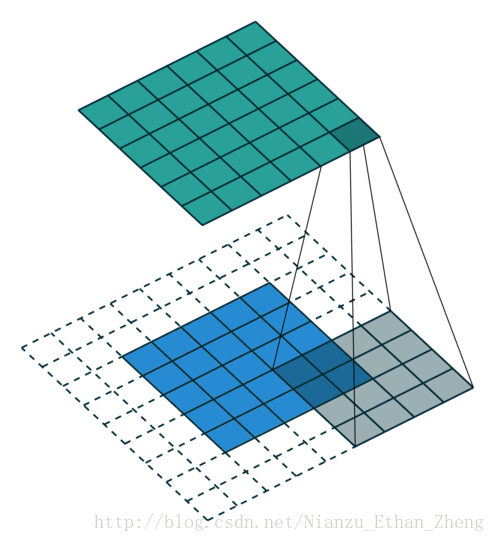
输入图像的大小为：

o=(i−k+2p)+1

第三种情况： 比较特殊，名为Half padding（SAME模式）
即是输出图像大小与输入图像大小相同, 假设 i=5,s=1,k=2n+1 ，
满足 p=[k/2] 有：

o=i+2[k/2]−(k−1)=i+2n−2n=i

第四种情况： Full padding，即输出比原始图像还大的图像，
满足 p=k−1,s=1 情况：

o=i+2(k−1)−(k−1)=i+k−1

第五种情况： s≠1,p=0
s=2,p=0,i=5,k=3

这种情况下输出图像大小为：

o=[i−ks]+1

注意的是：求 下限函数解释了最后一步并不和卷积层抵达输入另外一侧相一致。也就是会遗漏一些输入像素

第六种情况： s≠1,p≠0
输出图像大小为：

o=[i−k+2ps]+1

s=2,p=1,i=5,k=3

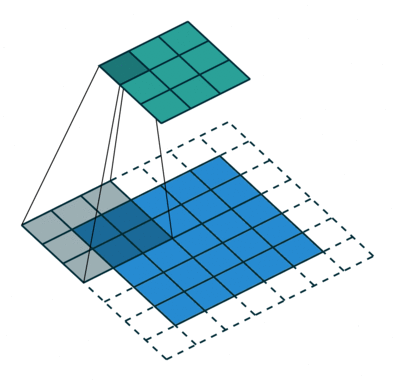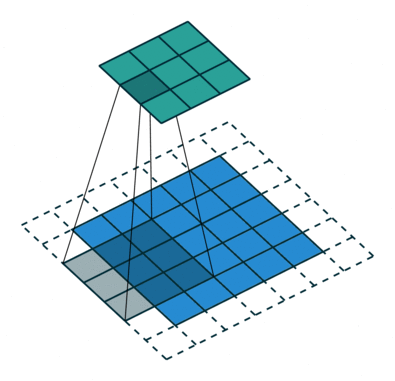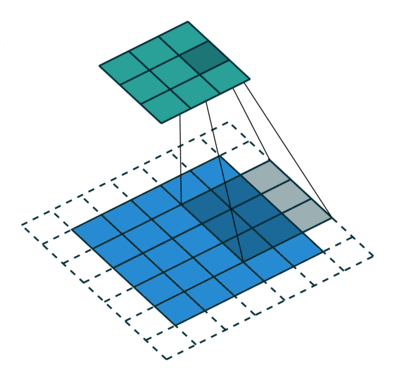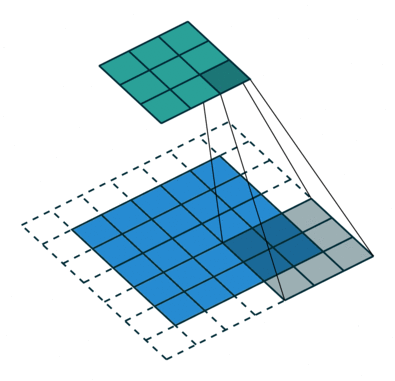
一个有趣的现象是：
假如 i−k+2ps=N 那么 j=i+a,a∈{0,1,...,s−1} 将会输出相同的大小。

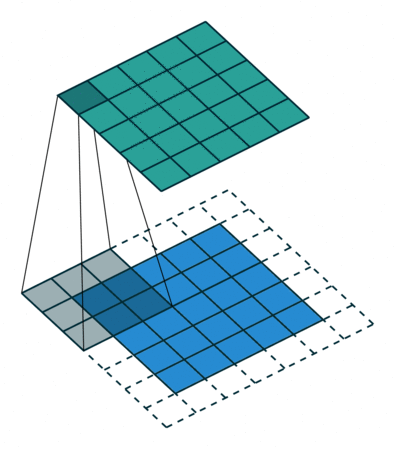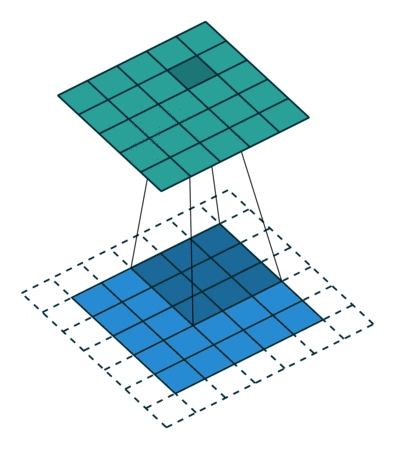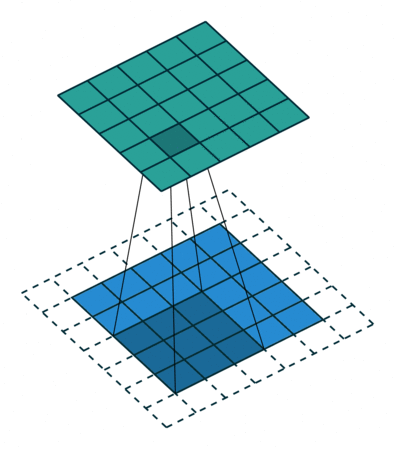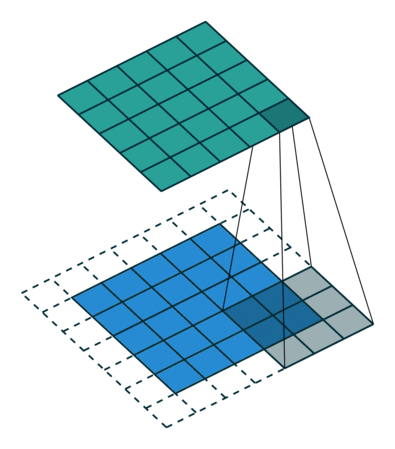
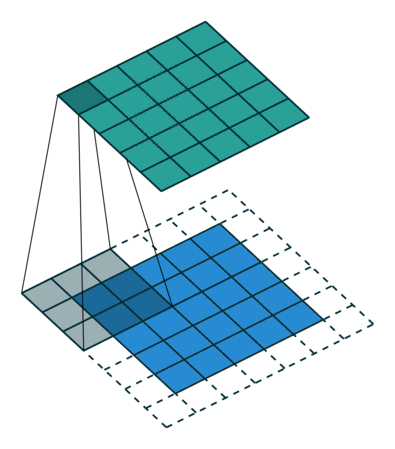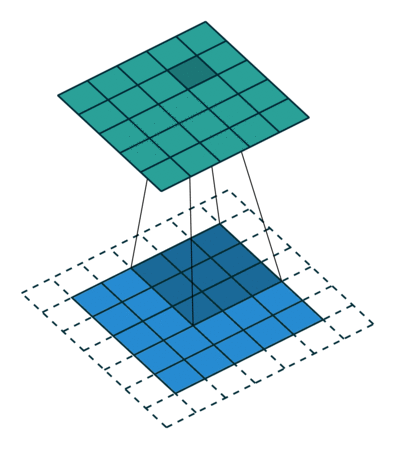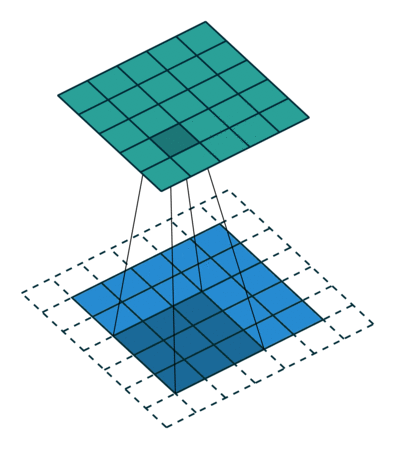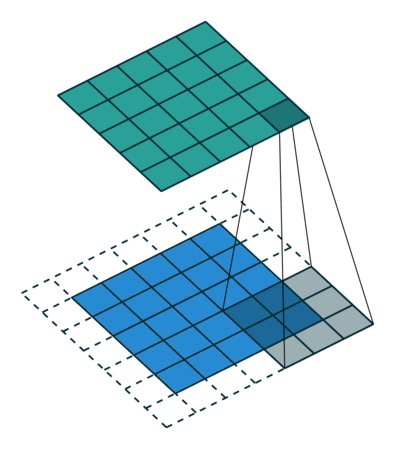
逆卷积过程

第一种情况：卷积操作 s=1,p=0,k

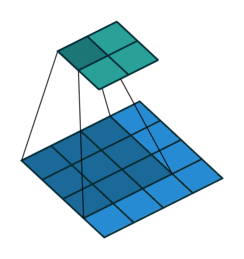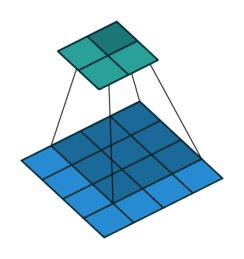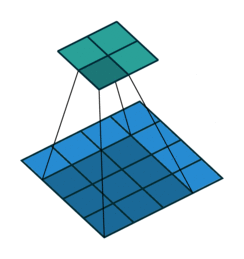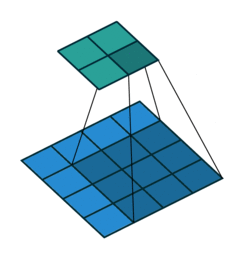
逆卷积操作 k′=k,s′=s,p′=k−1 相当于Full padding全填充模式

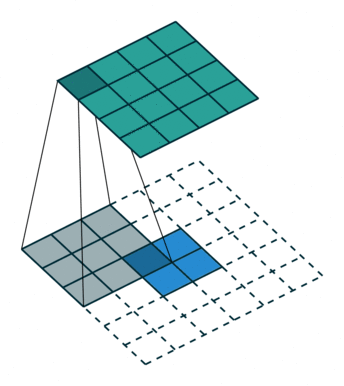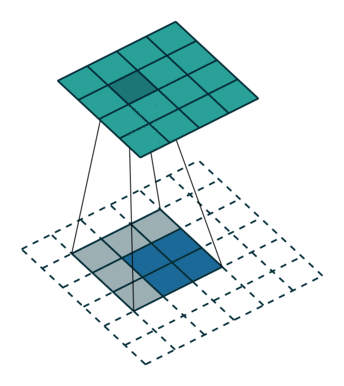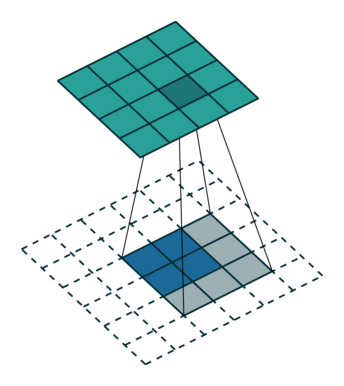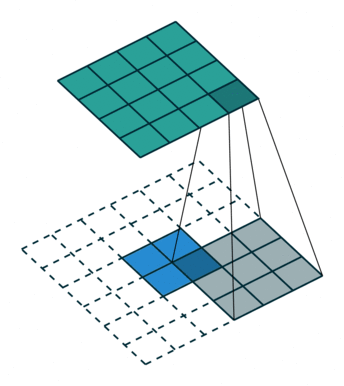
输出图像大小为：

o′=i′+(k−1)

第二种情况：明白上面非填充卷积等价于一个全零填充的逆卷积操作，因此，一般零填充的卷积操作等价于一个更少零填充的逆卷积操作。

i=5,k=4,p=2

开头结尾都减小p个，也就是：
s=1,k,p 可以描述为： k′=k,s′=s,p′=k−p−1

o′=i′+(k−1)−2p

第三种情况： 半填充的卷积（SAME模式情况下）
卷积 k=2n+1,n∈N,s=1 及 p=[k2]=n
逆卷积表示为：
k′=k,s′=s,p′=p

o′=i′+(k−1)−2p=i′+2n−2n=i′

第四种情况： 既然知道一个全填充逆卷积过程对应于无填充的卷积过程，那么可以推断一个全填充卷积过程对应一个无填充卷积过程：
全填充卷积 k，s=1 及 p=k−1
逆卷积表示为：
k′=k,s′=s,p′=0

o′=i′+(k−1)−2(k−1)=i′−(k−1)

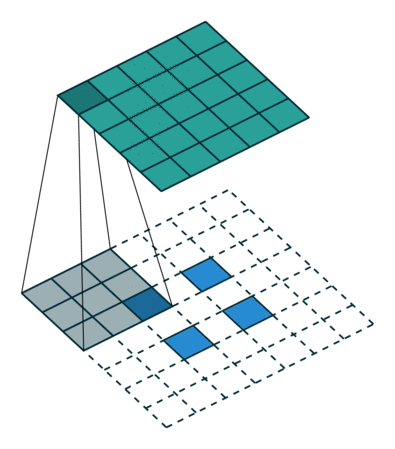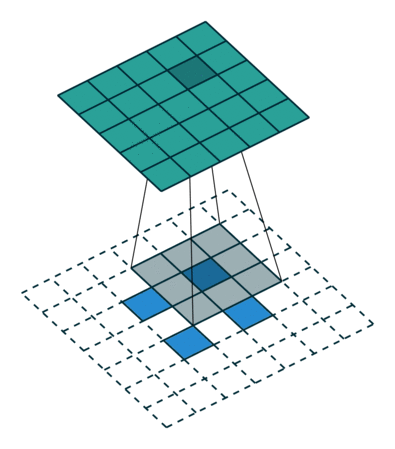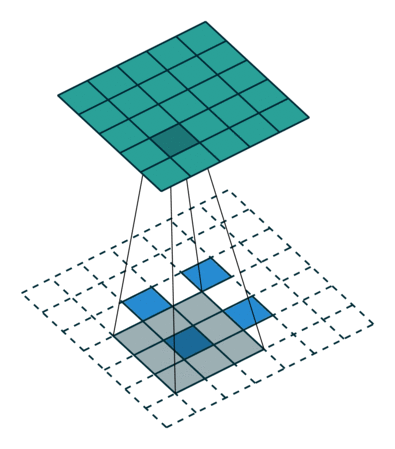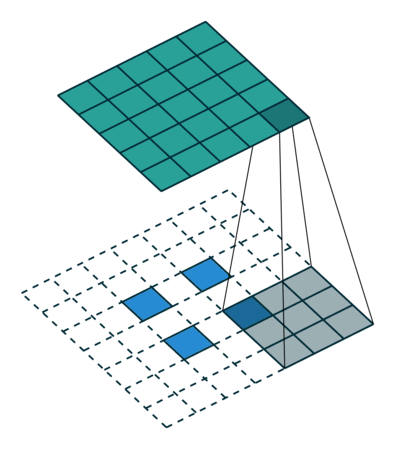
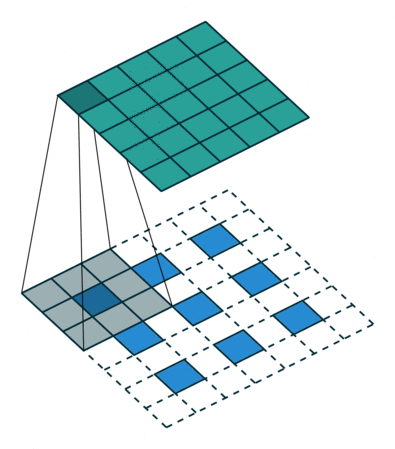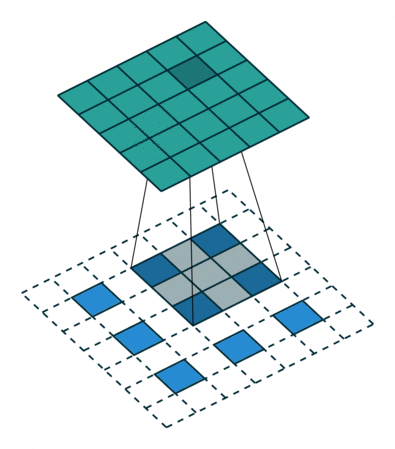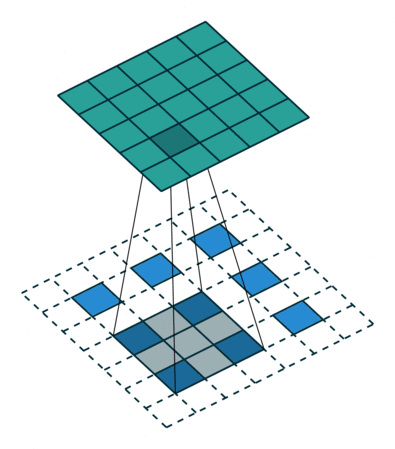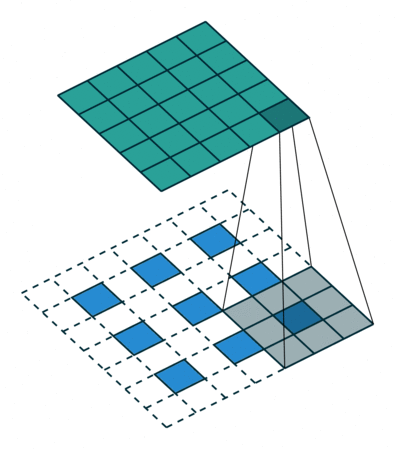
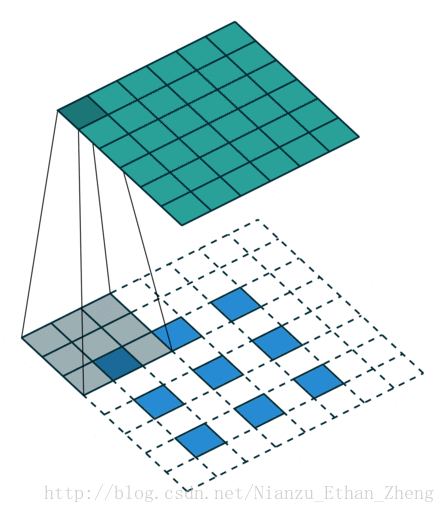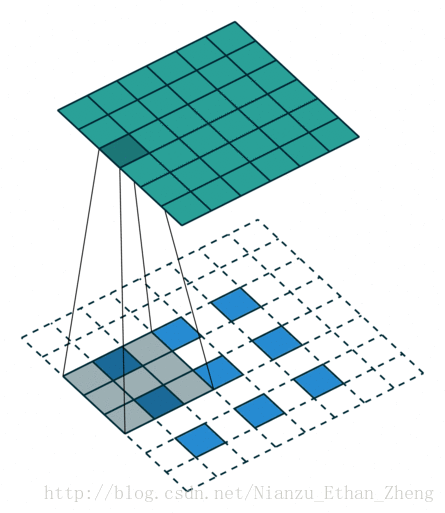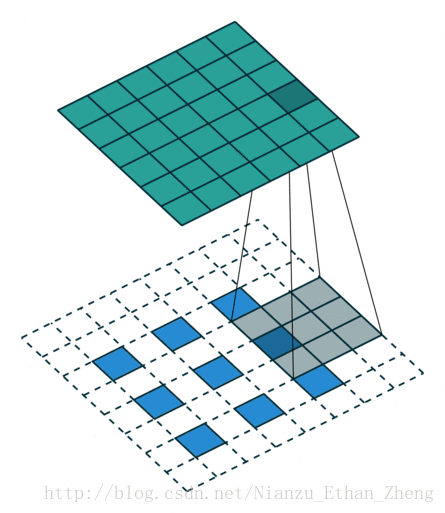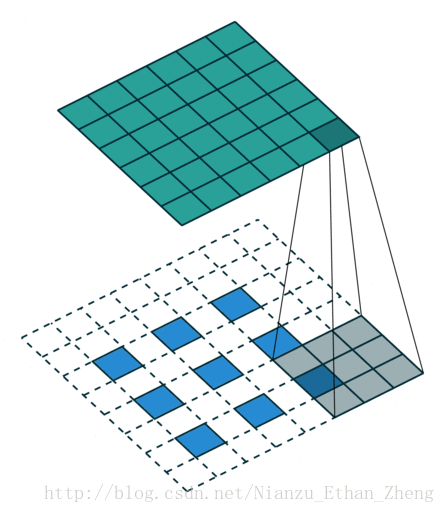
第五种情况： 对于 s>1 的卷积过程的逆过程等价于卷积过程 s<1 , 这要是为什么逆卷积过程被称为分数步长卷积（fractionally stride convolutions）
下面有一个例子：
i=5,k=3,s=2

这可以帮助理解为什么称为分数步长卷积，因为零填充在输入的单元中，让卷积核移动的速度比一个单元步长要慢的多。
可以先假设 p=0 , 输入的大小 i , 满足条件 i−ks=n,n∈N ,
那么逆卷积过程 i^′,k′=k,s′=1,p′=k−1 , 其中 i^′ 表示为在输入 i′ 的每个元素之间添加 s−1 零，也就是其输出大小为：

o′=s′(i′−1)+1+(k−1)=s′(i′−1)+k

第六种情况：零填充，步长 s>1 卷积，
卷积可以描述为： k,s,p 输入大小为： i+2p−ks=n,n∈N ,
与之对应的逆卷积过程表示为： i^′:k′=k,s′=1,p′=k−p−1
同理, i^′ 是在输入 i′ 的每个值间加入 s−1 个零，其输出为：

o′=s(i′−1)+k−2p

第七种情况： 零填充，步长 s>1 卷积，
卷积可以描述为： k,s,p 输入大小为： i+2p−ks≠n,n∈N ,
相当于对引入一个值 a∈{0,1,2,...,s−1} 使得 i+2p−k=ns+a,n∈N
这种情况下：
卷积描述为： k,s,p,a
与之对应的逆卷积过程表示为： i^′:k′=k,s′=1,p′=k−p−1
a=(i+2p−k)%s % 表示取余数
同理, i^′ 是在输入 i′ 的每个值间加入 s−1 个零，其输出为：

o′=s(i′−1)+a+k−2p

i=6,k=3,s=2,p=1

在Tensorflow上的思考：
tensorflow：tf.nn.conv2d_transpose

conv2d_transpose(
    value,             -->[batch, height, width, in_channels] for NHWC
    filter,            -->[height, width, output_channels, in_channels]
    output_shape,      -->A 1-D Tensor representing the output shape 
    strides,           -->A list of ints
    padding='SAME',    -->A string, either 'VALID' or 'SAME'.
    data_format='NHWC',
    name=None
)

其中 在卷积过程中，padding的方式分为两种：SAME与VALID

o={⌈is⌉⌈i−(k−1)s⌉Padding=′SAME′Padding=′VALID′

其实SAME模式下表达为 i−(k−1)+2p ，由于Half padding因此 −(k−1)+2p=0 ，所以表达成上式。
“VALID” only ever drops the right-most columns (or bottom-most rows).
“SAME” tries to pad evenly left and right, but if the amount of columns to be added is odd, it will add the extra column to the right, as is the case in this example (the same logic applies vertically: there may be an extra row of zeros at the bottom).

而在逆卷积过程中，只不过的是 s 为分数而已。
Tensorflow中逆卷积过程中两种方式均是指定卷积过程的Padding方式，可以看到源码中
Tensorflow 源码

gen_nn_ops.conv2d_backprop_input(input_sizes=output_shape_,
                                            filter=filter,
                                            out_backprop=value,
                                            strides=strides,
                                            padding=padding,
                                            data_format=data_format,
                                            name=name)

也就是tf.nn.conv2d_transpose 会根据制定输出大小和其他条件反推出输入大小，而该大小与真实输入大小不一致的话会出现报错。

举例子如下：
设定Valid模式下
i=3,k=3,s=2,p=0 ，设定 o′=4

可以反向计算出 o=⌈o′−(k−1)+2ps⌉=1

与 i=3 不一致因此会报错。

InvalidArgumentError (see above for traceback): Conv2DSlowBackpropInput: Size of out_backprop doesn't match computed: 
     actual = 3, computed = 1
     [[Node: conv2d_transpose_9 = Conv2DBackpropInput[T=DT_FLOAT, data_format="NHWC", padding="VALID", strides=[1, 2, 2, 1], use_cudnn_on_gpu=true, _device="/job:localhost/replica:0/task:0/gpu:0"](conv2d_transpose_9/output_shape, Const_19, Const_18)]]

仅设定 o′=7，8 ，可以通过反向传过去，不会报错

在SAME模式下（Half Padding）：

i=3,k=3,s=2，p=1 ，设定 o′=4

可以反向计算出 o=⌈o′−(k−1)+2ps⌉=2

InvalidArgumentError (see above for traceback): Conv2DSlowBackpropInput: Size of out_backprop doesn't match computed:
     actual = 3, computed = 2
     [[Node: conv2d_transpose_14 = Conv2DBackpropInput[T=DT_FLOAT, data_format="NHWC", padding="VALID", strides=[1, 2, 2, 1], use_cudnn_on_gpu=true, _device="/job:localhost/replica:0/task:0/gpu:0"](conv2d_transpose_14/output_shape, Const_29, Const_28)]]

仅满足 o′=⌈o′−(k−1)+2ps⌉=i ，可以通过反向传过去，不会报错

⌈o′−(k−1)+2ps⌉(i−1)s<o′−(k−1)+(i−1)s+(k−1)−2p<o′≤=s2p≤isis+(k−1)−2p

也就是当 o′=5，6 时可以通过反向传过去，不会报错
Reference:

Theano Manual