经典算法之—模拟退火
一.爬山算法
介绍模拟退火前,先介绍爬山算法。爬山算法是一种简单的贪心搜索算法,该算法每次从当前解的临近解空间中选择一个最优解作为当前解,直到达到一个局部最优解。
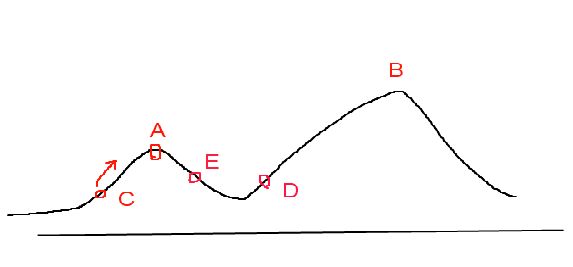
爬山算法实现很简单,其主要缺点是会陷入局部最优解,而不一定能搜索到全局最优解。如图1所示:假设C点为当前解,爬山算法搜索到A点这个局部最优解就会停止搜索,因为在A点无论向那个方向小幅度移动都不能得到更优的解。
图1
二.模拟退火
爬山法是完完全全的贪心法,每次都鼠目寸光的选择一个当前最优解,因此只能搜索到局部的最优值。模拟退火其实也是一种贪心算法,但是它的搜索过程引入了随机因素。
模拟退火算法以一定的概率来接受一个比当前解要差的解,因此有可能会跳出这个局部的最优解,达到全局的最优解。
以图1为例,模拟退火算法在搜索到局部最优解A后,会以一定的概率接受到E的移动。也许经过几次这样的不是局部最优的移动后会到达D点,于是就跳出了局部最大值A。
既然模拟退火具有概率性放弃当前最优解,接受更差的解。那么这个概率如何定义呢。关于模拟退火的定义,其实也是“模拟退火”名称的来源。
模拟退火算法是模拟热力学系统中的退火过程,因此他是一种启发式算法。其原因就是受启发于“热力学的物体高温冷却退火过程”。在退火过程中是将目标函数作为能量函数。大致过程如下:初始高温 => 温度缓慢下降=> 终止在低温 (这时能量函数达到最小,目标函数最小)。
在热力学中的退火过程大致是变温物体缓慢降温而达到分子之间能量最低的状态。设热力学系统S中有有限个且
离散的n个状态,状态i的能量为Ei,在温度Tk下,经过一段时间达到热平衡,这时处于状态i的概率为:
其中Ck为常数。
受热力学启发,我们定义了模拟退火的概率表达式:
所谓能量可大概理解为被优化函数的值,温度理解为自变量。值得注意的是,虽然模拟退火会概率性的接受比当前解更差的解,但是这相对于完全贪心的爬山算法来说,其搜索范围无疑扩大了,以此获得全局最优解的概率大大提高。理论上来说,只要优化过程,满足初始温度足够高、降温速度足够慢、终止温度足够低,那么模拟退火最终会以概率1收敛到全局最优解(因此理论上就不需要记录历史最优解)。
但是这无疑是在极限下的情况,现实中是无法办到的。因此我们在模拟退火的过程一定要记录历史最优解。下面来一个例题:
http://acm.hdu.edu.cn/showproblem.php?pid=2899
Now, here is a fuction:
F(x) = 6 * x^7+8*x^6+7*x^3+5*x^2-y*x (0 <= x <=100)。Can you find the minimum value when x is between 0 and 100.
题目的解为:
input:100;output:-74.4291
input:200;output:-178.8534
下面是代码:
############################
#模拟退火求函数最小值
#by:zkj
#2016年12月17日
############################
from numpy import random
from math import exp
from time import clock
def getFun(x,y): ##获取函数值
return 6*x**7 + 8*x**6 + 7*x**3 + 5*x**2 - x*y
def getRand(): ##获取随机概率
return random.random()
def SA(initT,y,step,overT): ##模拟退火过程
minFunVal = getFun(initT,y)
T = initT
historyMinVal = minFunVal #存放历史最优解
while not((T - overT) >= 0 and (T - overT) <= 10**-3):
T = T * step #更新温度
FunVal = getFun(T,y)
if minFunVal >= FunVal: ##获得更好的解,接受
minFunVal = FunVal
else: ##获得更差的解,一定概率接受
if exp((minFunVal - FunVal) / T) >= getRand():
minFunVal = FunVal
if minFunVal < historyMinVal:
historyMinVal = minFunVal
return historyMinVal
startTime = clock()
initT = 100 #初始温度
y = 200 #初始参数
step = 0.99 #降温步长
overT = 0 #最低温度
print("最小值为:\n",SA(initT,y,step,overT))
runTime = clock() - startTime
print("运行时间为:\n",runTime)参考文献:
http://www.cnblogs.com/heaad/archive/2010/12/20/1911614.html