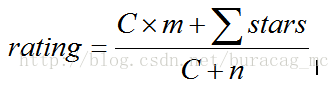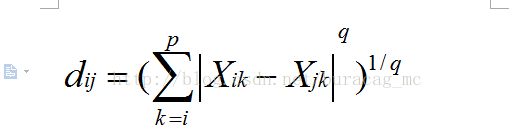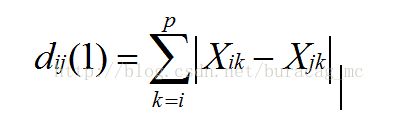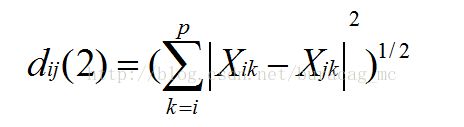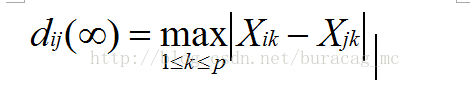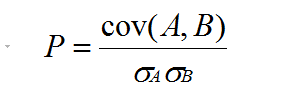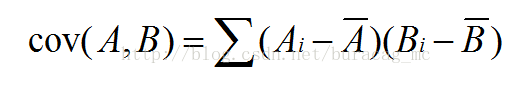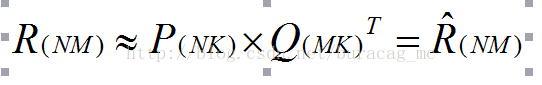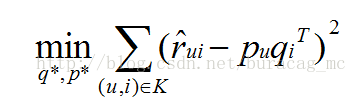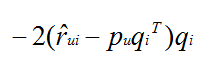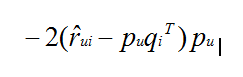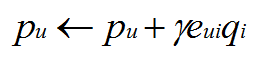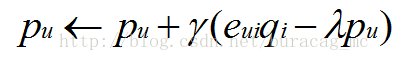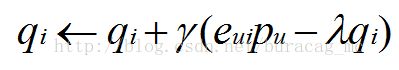【Python】 大规模电影推荐
同步至https://www.runblog.online/2019/03/20/a-simple-collaborative-filtering-framework/
简介
推荐系统把我们从洪水般泛滥的信息中解放出来,为我们制定了个性化的信息流。网易云音乐、电子商务平台等都从推荐系统中获益颇多。推荐系统的实现是如此简单,但是在数据量稀疏师很容易产生怪异的结果和过拟合。
最简单最容易理解的方法就是看一下所信赖的人有哪些偏好,从中得到我们的推荐。协同过滤便是这一类推荐系统技术的基础。简单来说,他是基于这样一个假设:那些和你有共同偏好的人将来也会和你拥有共同偏好;这是从人的角度来看。另一个推论是基于物品的角度——那些被同一个人所喜爱的物品很有可能出现在另一个人喜爱的物品中。这就是我们常说的基于人的协同过滤以及基于物品的协同过滤。
对偏好建模
举个简单例子:两个人A和B,他们对同一个物品有着共同的偏好。如果A对另外一件物品如游戏机感兴趣,那么和任意选一个物品相比,B更有可能也对游戏机感兴趣。而我们相信,A和B的共同偏好可以从他们大量的已有偏好中发现。通过协同过滤的分组特性,我们可以对这个世界的物品进行过滤。
最长用的偏好表达模型把排名的问题简化成对偏好进行数值化的过程。比如:
- 布尔值(是或者否)
- 顶和踩(比如反对、讨厌)
- 加权信息(点击数或者动作数)
- 广泛的分类排名(星数从讨厌到喜爱)。
这些方法都是为了能够对个体的偏好情况进行数值化,以便后面模型的建立。
数据的加载
1.从http://grouplens.org/datasets/movielens/下载数据集100K(ml-100K.ZIP)。
2.解压数据到工作路径。
3.为了了解包括用户评分的u.data和电影详细信息的u.item连个文件。利用windows下的more命令来观察数据。(Mac和Linux下的head命令)
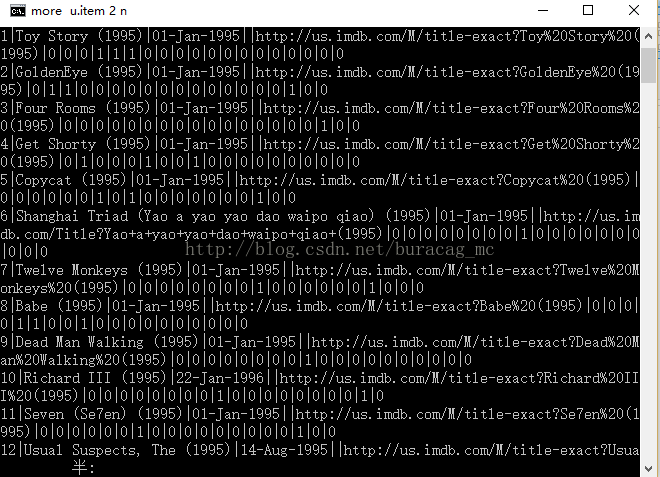
more u.item 2
more u.data
对于u.data,第一列为用户ID,第二列为电影ID,第三列为评分,第四列为时间戳;u.item文中包括电影ID、标题、上映时间和IMDB链接。此外,文件中还用一个布尔值组标识的每部电影的类型,包括动作、探险、动画、儿童、喜剧、犯罪、记录、虚幻、黑丝、恐吓、音乐、推理、浪漫、科幻、惊悚、战争和西部。
OK,下面正式进入正题~~~
1.将电影数据导入
#encoding:utf-8
import os
import csv
import heapq
from operator import itemgetter
from datetime import datetime
from collections import defaultdict
def load_reviews(path, **kwargs):
'''
加载电影数据文件
'''
options = {
'fieldnames': ('userid', 'movieid', 'rating', 'timestamp'),
'delimiter' : '\t'
}
options.update(kwargs)
parse_date = lambda r, k: datetime.fromtimestamp(float(r[k]))
parse_int = lambda r, k: int(r[k])
with open(path, 'rb') as reviews:
reader = csv.DictReader(reviews, **options)
for row in reader:
row['movieid'] = parse_int(row, 'movieid')
row['userid'] = parse_int(row, 'userid')
row['rating'] = parse_int(row, 'rating')
row['timestamp'] = parse_date(row, 'timestamp')
yield row
2.创建一个辅助函数来辅助函数导入:
def relative_path(path):
'''
辅助数据导入
'''
dirname = os.path.dirname(os.path.realpath('__file__'))
path = os.path.join(dirname, path)
return os.path.normpath(path)
3.导入电影信息
def load_movies(path, **kwargs):
'''
读取电影信息
'''
options = {
'fieldnames': ('movieid', 'title', 'release', 'video', 'url'),
'delimiter' : '|',
'restkey' : 'genre'
}
options.update(**kwargs)
parse_int = lambda r,k: int(r[k])
parse_date = lambda r,k: datetime.strptime(r[k], '%d-%b-%Y') if r[k] else None
with open(path, 'rb') as movies:
reader = csv.DictReader(movies, **options)
for row in reader:
row['movieid'] = parse_int(row, 'movieid')
#print row['movieid']
row['release'] = parse_date(row, 'release')
#print row['release']
#print row['video']
yield row4.创建一个类,在之后的分析中将会反复用到
class MovieLens(object):
def __init__(self, udata, uitem):
self.udata = udata
self.uitem = uitem
self.movies = {}
self.reviews = defaultdict(dict)
self.load_dataset()
def load_dataset(self):
#加载数据到内存中,按ID为索引
for movie in load_movies(self.uitem):
self.movies[movie['movieid']] = movie
for review in load_reviews(self.udata):
self.reviews[review['userid']][review['movieid']] = review
#print self.reviews[review['userid']][review['movieid']]
5.测试
输入以下代码进行测试。
if __name__ == '__main__':
data = relative_path('data/ml-100k/u.data')
item = relative_path('data/ml-100k/u.item')
model = MovieLens(data, item)
寻找高评分电影
函数reviews_for_movie()遍历所有评分字典中的值(通过userid进行索引),并检查用户是否对当前的movieid进行过评分,如存在,则将评分结果返回.
def reviews_for_movie(self, movieid):
for review in self.reviews.values():
if movieid in review: #存在则返回
yield review[movieid]函数average_reviews(),返回电影ID、平均得分以及评分的个数。
def average_reviews(self):
#对所有的电影求平均水平
for movieid in self.movies:
reviews = list(r['rating'] for r in self.reviews_for_movie(movieid))
average = sum(reviews) / float(len(reviews))
yield (movieid, average, len(reviews)) #返回了(movieid,评分平均分,长度(即评价人数))toprated函数利用heapq对结果根据平均分进行排序。
def top_rated(self, n=10):
#返回一个前n的top排行
return heapq.nlargest(n, self.bayesian_average(), key=itemgetter(1))基于贝叶斯的电影评分算法,由于朴素的贝叶斯平均值算法无法对那些有较多评分数的电影之间产生有意义的比较。我们需要给每个电影一个统一 的标准分数:
这里n是预设值,C是我们通过
C = float(sum(num for mid, avg, num in model.average_reviews())) / len(model.movies)得到的,这里直接给出m为3,C为59。
def bayesian_average(self, c=59, m=3):
#返回一个修正后的贝叶斯平均值
for movieid in self.movies:
reviews = list(r['rating'] for r in self.reviews_for_movie(movieid))
average = ((c * m) + sum(reviews)) / float(c + len(reviews))
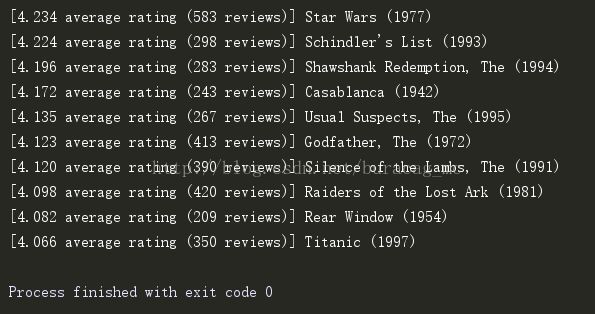
yield (movieid, average, len(reviews))输出排名前十的电影
if __name__ == '__main__':
data = relative_path('data/ml-100k/u.data')
item = relative_path('data/ml-100k/u.item')
model = MovieLens(data, item)
for mid, avg, num in model.top_rated(10):
title = model.movies[mid]['title']
print "[%0.3f average rating (%i reviews)] %s" % (avg, num,title)
计算用户在偏好空间中的距离
基于用户的协同过滤以及基于物品的协同过滤是推荐系统中最常用的两种协同过滤方式。我们把偏好空间想象成一组用户或物品的N维特征空间,这样我们就可以比较用户或者物品在向量空间中是否邻近,因此这类协同过滤系统又被称为最近邻推荐系统。
显然,构建这类系统最关键的一步就是找到一种相似性或者距离的度量标准,我们可以根据这类标准衡量对物品的偏好程度。常见的这类标准有欧式距离、曼哈顿距离、余弦距离、皮尔逊相关系数等、斯皮尔曼相关度等。
下面我们利用欧式距离来构建。
函数share_preferences()将找出两个用户A和B共同评分过的电影。
def share_preferences(self, criticA, criticB):
'''
找出两个评论者之间的交集
'''
if criticA not in self.reviews:
raise KeyError("Couldn't find critic '%s' in data " % criticA)
if criticB not in self.reviews:
raise KeyError("Couldn't find critic '%s' in data " % criticB)
moviesA = set(self.reviews[criticA].keys())
moviesB = set(self.reviews[criticB].keys())
shared = moviesA & moviesB
#创建一个评论过的的字典返回
reviews = {}
for movieid in shared:
reviews[movieid] = (
self.reviews[criticA][movieid]['rating'],
self.reviews[criticB][movieid]['rating'],
)
return reviews函数euclidean_distance()通过他们的共同电影偏好作为向量来计算两个用户之间的欧式距离
在这里我补充一下:
*闵可夫斯基距离,简称闵氏距离;
按q值的不同又分成
(1)绝对距离,即曼哈顿距离(q=1)
(2)欧几里得距离(q=2)
(3)切比雪夫距离(q=无穷)
def euclidean_distance(self, criticA, criticB, prefs='users'):
'''
通过两个人的共同偏好作为向量来计算两个用户之间的欧式距离
'''
#创建两个用户的交集
preferences = self.share_preferences(criticA,criticB)
#没有则返回0
if len(preferences) == 0: return 0
#求偏差的平方的和
sum_of_squares = sum([pow(a-b,2) for a,b in preferences.values()])
#修正的欧式距离,返回值的范围为[0,1]
return 1 / (1 + sqrt(sum_of_squares))最后,照例输入代码测试一下。
if __name__ == '__main__':
data = relative_path('data/ml-100k/u.data')
item = relative_path('data/ml-100k/u.item')
model = MovieLens(data, item)
print model.euclidean_distance(631,532) #A,B结果为0.240253073352。
计算用户相关性
这部分将利用皮尔逊相关系数来作为度量指标。函数pearson_correlation计算用户A和用户B的皮尔逊相关系数。
这里给出皮尔逊相关系数的计算公式:
经过整理我们具体计算相关系数是,可以用如下公式:
def pearson_correlation(self, criticA, criticB, prefs='users'):
'''
返回两个评论者之间的皮尔逊相关系数
'''
if prefs == 'users':
preferences = self.share_preferences(criticA, criticB)
elif prefs == 'movies':
preferences = self.shared_critics(criticA, criticB)
else:
raise Exception("No preferences of type '%s'." % prefs)
length = len(preferences)
if length == 0 :return 0
#循环处理每一个评论者之间的皮尔逊相关系数
sumA = sumB = sumSquareA = sumSquareB = sumProducts = 0
for a, b in preferences.values():
sumA += a
sumB += b
sumSquareA += pow(a, 2)
sumSquareB += pow(b, 2)
sumProducts += a * b
#计算皮尔逊系数
numerator = (sumProducts * length) - (sumA * sumB)
denominator = sqrt(((sumSquareA*length) - pow(sumA,2)) * ((sumSquareB*length) - pow(sumB,2)))
if denominator == 0:return 0
return abs(numerator/denominator)同理,用如下代码测试一下:
if __name__ == '__main__':
data = relative_path('data/ml-100k/u.data')
item = relative_path('data/ml-100k/u.item')
model = MovieLens(data, item)
print model.pearson_correlation(232,532)结果为0.062025793538385047
为特定用户寻找最好的影评人
在已经有两种不同的衡量指标来计算两个用户之间的相似程度,接下来我们为一个特定用户寻找最适合他的影片人,看一下两者在洗好空间上的相似程度。
函数similar_critics()来寻找最匹配的用户。
def similar_critics(self,user, metric='euclidean', n=None):
'''
为特定用户寻找一个合适的影评人
'''
metrics = {
'euclidean': self.euclidean_distance,
'pearson': self.pearson_correlation
}
distance = metrics.get(metric, None)
#解决可能出现的状况
if user not in self.reviews:
raise KeyError("Unknown user, '%s'." % user)
if not distance or not callable(distance):
raise KeyError("Unknown or unprogrammed distance metric '%s'." % metric)
#计算对用户最合适的影评人
critics = {}
for critic in self.reviews:
#不能与自己进行比较
if critic == user:
continue
critics[critic] = distance(user,critic)
if n:
return heapq.nlargest(n, critics.items(), key=itemgetter(1))
return critics下面利用如下代码分别测试一下两种度量指标的结果:
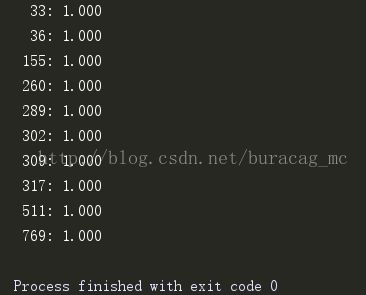
for item in model.similar_critics(232, 'pearson', n=10):
print "%4i: %0.3f" % item for item in model.similar_critics(232, 'euclidean', n=10):
print "%4i: %0.3f" % item结论
皮尔逊系数会比欧式距离找到更多的相似用户。欧式距离更倾向于那些评分完全一致的用户,而皮尔逊相关性更倾向于线性相关用户的相似性,因此能纠正分数膨胀现象:两个一个用户总是比另一个用户评分高一星;
因此仅仅用那些相似用户的评分无法预测一个用户对一个新电影的评分,我们必须通过所有用户的打分情况才能对用户的评分做出预测。
预测用户评分
为了预测一个电影的评分,我们需要计算评论过这个电影的用户的评分相对当前用户的加权平均值。权重为那些评论过分的用户和当前用户的相似程度,很显然,我们认为和当前用户相似程度越高的用户的评分应被给予更大的权重。
predict_ranking函数基于其他用户的评分预测当前用户对电影可能的评分。
def predict_ranking(self, user,movie, metric='euclidean', critics=None):
'''
预测一个用户对一部电影的评分,相当于评论过这部电影的用户对当前用户的加权均值
并且权重取决与其他用户和该用户的相似程度
'''
critics = critics or self.similar_critics(user,metric=metric)
total = 0.0
simsum = 0.0
for critic, similarity in critics.items():
if movie in self.reviews[critic]:
total += similarity * self.reviews[critic][movie]['rating']
simsum += similarity
if simsum == 0.0 :return 0.0
return total / simsum接下predict_all_rankings函数来就可以预测所有电影的评分。
def predict_all_rankings(self,user,metric='euclidean', n=None):
'''
为所有的电影预测评分,返回前n个评分的电影和它们的评分
'''
critics = self.similar_critics(user, metric=metric)
movies = {
movie:self.predict_ranking(user, movie, metric, critics)
for movie in self.movies
}
if n:
return heapq.nlargest(n, movies.items(), key=itemgetter(1))
return movies同理,接下来输入以下代码进行测试:
print model.predict_ranking(422, 50,'euclidean')
print model.predict_ranking(422,50,'pearson')结果如下:
predict_all_rankings函数根据传入的度量指标预测一个特定用户对所有电影的排名,并接受一个参数n来返回排名前n的电影。
for mid ,rating in model.predict_all_rankings(578,'pearson',10):
print '%0.3f: %s' % (kerating, model.movies[mid]['title'])基于物品的协同过滤
前文都是基于用户间的相似度来进行预测,然而相似度空间我们知道可以从两个角度去探索。以用户为中心的协同过滤的洗好空间中以用户为数据点,比较用户之间的相似程度,并利用相似程度寻找和用户相似的用户作为预测的因素;另一种以物品为中心的协同过滤洗好空间中以物品为数据点,推荐系统根据一组物品和另一组物品的相似程度做推荐。
另外,由于物品之间的相似性变化较为缓慢,因此基于物品的协同过滤是一种常用的推荐优化方案。
函数shared_critics类似于函数shared_preferences,不同的是函数shared_preferences将找出两个用户A和B共同评分过的电影。而函数shared_critics将找出两部电影有共同的用户。函数similar_items与函数similar_critics类似,是为了寻找最合适的电影而不是寻找合适的用户。
def shared_critics(self, movieA, movieB):
'''
返回两部电影的交集,即两部电影在同一个人观看过的情况
'''
if movieA not in self.movies:
raise KeyError("Couldn't find movie '%s' in data" % movieA)
if movieB not in self.movies:
raise KeyError("Couldn't find movie '%s' in data" % movieB)
criticsA = set(critic for critic in self.reviews if movieA in self.reviews[critic])
criticsB = set(critic for critic in self.reviews if movieB in self.reviews[critic])
shared = criticsA & criticsB #和操作
#创建一个评论过的字典以返回
reviews = {}
for critic in shared:
reviews[critic] = (
self.reviews[critic][movieA]['rating'],
self.reviews[critic][movieB]['rating']
)
return reviews
def similar_items(self, movie, metric='eculidean', n=None):
metrics = {
'euclidean': self.euclidean_distance,
'pearson': self.pearson_correlation,
}
distance = metrics.get(metric, None)
#解决可能出现的状况
if movie not in self.reviews:
raise KeyError("Unknown movie, '%s'." % movie)
if not distance or not callable(distance):
raise KeyError("Unknown or unprogrammed distance metric '%s'." % metric)
items = {}
for item in self.movies:
if item == movie:
continue
items[item] = distance(item, movie,prefs='movies')
if n:
return heapq.nlargest(n, items.items(), key=itemgetter(1))
return items同理,输入以下代码进行测试:
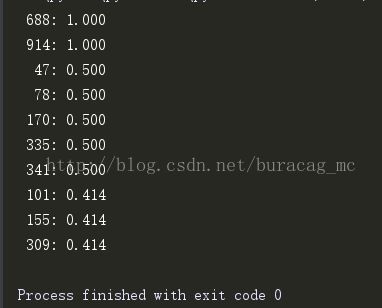
for movie, similarity in model.similar_items(631, 'pearson').items():
print '%0.3f : %s' % (similarity, model.movies[movie]['title'])结果如下:
同理按照前面预测用户评分的思想,基于已经计算好的相似性,我们可以按照下面 的方法进行推荐。
def predict_items_recommendation(self, user, movie, metric='euclidean'):
movie = self.similar_items(movie, metric=metric)
total = 0.0
simsum = 0.0
for relmovie, similarity in movie.items():
if relmovie in self.reviews[user]:
total += similarity * self.reviews[user][relmovie]['rating']
simsum += similarity
if simsum == 0.0:return 0.0
return total / simsum同理,输入以下代码进行测试:
print model.predict_items_recommendation(232, 52, 'pearson')结果为3.980443976。
OK,宿舍马上熄灯了,暂且写到这儿吧,后面还有一些内容,再更新吧~~
=======================================4.24更新========================================
建立并训练SVD模型
算法原理简介
由于协同过滤方法或者不能处理非常大的数据集,或者处理不好用户评论非常少的情况(即我们所说的数据比较稀疏的情况)。矩阵分解方法可以方便地随着观测数据进行线性扩展。
矩阵分解(SVD)的目的是将原有矩阵拆解为两个矩阵,通过它们的点技(内积、向量积)和原有矩阵相似。在这里,我们的训练矩阵为用户到电影评分的一个NxM矩阵,用户没用评分的电影的值为空或者0。我们希望通过矩阵分解模型能够以点积填补那些空值,作为用户对电影评分的预测值。即:
并用下面的公式对用户u对电影i的评分进行估计:
为了实现对P和Q的估计,仅需要对qi和pu进行估计,可以最优化有一下目标函数完成:
式中,K为训练集当中所有的已知的用户、电影评分(即观测到的评分部分)
有很多方法对以上目标函数进行求解,通常我们采用随机梯度下降法(SGD,网上很多相关的~后面再写下对SGD的总结吧)求解,通过不断迭代更新参数和预测值的方法进行参数估计,使得误差逐步变小。通过这种方法希望能找到一个局部最优解,使得误差在可接受的范围内。
所以参数更新方向朝梯度相反方向前进一小步:
通常,随机梯度下降方法同样可以对改进后的模型进行参数估计,其具体迭代更新公式为:
其中是一个惩罚参数。
矩阵分解算法对内存的利用效率极高,可以并行,支持多特征向量。并且可以设置不同的置信级别。优点是显而易见的~
训练SVD模型
下面附上训练SVD模型的代码:
def factor2(R, P=None, Q=None, K=2, steps=5000, alpha=0.0002, beta=0.02):
"""
依靠给定的参数训练矩阵R.
:param R: N x M的矩阵,即将要被训练的
:param P: 一个初始的N x K矩阵
:param Q: 一个初始的M x K矩阵
:param K: 潜在的特征
:param steps: 最大迭代次数
:param alpha: 梯度下降法的下降率
:param beta: 惩罚参数
:returns: P 和 Q
"""
if not P or not Q:
P, Q = initialize(R, K)
Q = Q.T
rows, cols = R.shape
for step in xrange(steps):
eR = np.dot(P, Q) # 一次性内积即可
for i in xrange(rows):
for j in xrange(cols):
if R[i,j] > 0:
eij = R[i,j] - eR[i,j]
for k in xrange(K):
P[i,k] = P[i,k] + alpha * (2 * eij * Q[k,j] - beta * P[i,k])
Q[k,j] = Q[k,j] + alpha * (2 * eij * P[i,k] - beta * Q[k,j])
eR = np.dot(P, Q) # Compute dot product only once
e = 0
for i in xrange(rows):
for j in xrange(cols):
if R[i,j] > 0:
e = e + pow((R[i,j] - eR[i,j]), 2)
for k in xrange(K):
e = e + (beta/2) * (pow(P[i,k], 2) + pow(Q[k,j], 2))
if e < 0.001:
break
return P, Q.T导出SVD模型至硬盘
由于SVD模型训练需要很长的时间,我们可以先创建一个从硬盘导入导出模型的机制。如果可以把矩阵分解的系数进行保存,并在需要的时候进行服用。这时我们就要利用Python的pickle模块来进行方便地处理了~
class Recommender(object):
@classmethod
def load(klass, pickle_path):
'''
接受磁盘上包含pickle序列化后的文件路径为参数,并用pickle模块载入文件。
由于pickle模块在序列化是会保存导出时对象的所有属性和方法,因此反序列
化出来的对象有可能已经和当前最新代码中的类不同。
'''
with open(pickle_path, 'rb') as pkl:
return pickle.load(pkl)
def __init__(self, udata):
self.udata = udata
self.users = None
self.movies = None
self.reviews = None
# 描述性工程
self.build_start = None
self.build_finish = None
self.description = None
self.model = None
self.features = 2
self.steps = 5000
self.alpha = 0.0002
self.beta = 0.02
self.load_dataset()
def dump(self,pickle_path):
'''
序列化方法、属性和数据到硬盘,以便在未来导入
'''
with open(pickle_path, 'wb' ) as pkl:
pickle.dump(self,pkl)
def load_dataset(self):
'''
加载用户和电影的索引作为一个NxM的数组,N是用户的数量,M是电影的数量;标记这个顺序寻找矩阵的价值
'''
self.users = set([])
self.movies = set([])
for review in load_reviews(self.udata):
self.users.add(review['userid'])
self.movies.add(review['movieid'])
self.users = sorted(self.users)
self.movies = sorted(self.movies)
self.reviews = np.zeros(shape=(len(self.users), len(self.movies)))
for review in load_reviews(self.udata):
uid = self.users.index(review['userid'])
mid = self.movies.index(review['movieid'])
self.reviews[uid, mid] = review['rating']
def build(self, output=None):
'''
训练模型
'''
options = {
'K' : self.features,
'steps' : self.steps,
'alpha' : self.alpha,
'beta' : self.beta
}
self.build_start = time.time()
nnmf = factor2
self.P, self.Q = nnmf(self.reviews, **options)
self.model = np.dot(self.P, self.Q.T)
self.build_finish = time.time()
if output :
self.dump(output)在做完以上步骤后,就慢慢等着模型训练吧~
最后,利用数据集测试一下SVD模型,输入以下代码利用模型来访问预测的评分:
#利用模型来访问预测的评分
def predict_ranking(self, user, movie):
uidx = self.users.index(user)
midx = self.movies.index(movie)
if self.reviews[uidx, midx] > 0:
return None
return self.model[uidx, midx]并将电影做一个排名系统:
#预测电影的排名
def top_rated(self, user, n=12):
movies = [(mid, self.predict_ranking(user, mid)) for mid in self.movies]
return heapq.nlargest(n, movies, key=itemgetter(1))
至此,一个完整的电影推荐系统的框架基本搭建完成,后面就是数据集(库)的更新,以及定期训练SVD模型了~~