数据结构与算法分析-C++描述 第5章 散列ADT（开放定址法）

开放定址法：  

     在上一篇数据结构与算法分析-C++描述 第5章 散列ADT（分离链接法）中提出散列的基本思想、散列函数以及解决冲突的两种方法：分离链接法和开放定址法，完成了分离链接法的实例应用，本篇承接上篇，实现开放定址法的实例应用。

    分离链接法的缺点是使用了一些链表，由于给新单元分配地址需要时间（特别是在高级语言中），因此这导致了算法速度的下降，同时算法还要求第二种数据结构的实现。使用链表解决冲突的另一个方法是当冲突发生时尝试选择另一个存储单元，直到找到空的单元。更正式的，,依次进行尝试，其中,函数成为冲突解决函数。开放定址法法是不使用链表的散列实现，通常通常装填因子,这样的表称为探测散列表（probing hash tables）,探测散列表解决冲突的常见方法：线性探测、平方探测、双散列。

线性探测：

平方探测： 

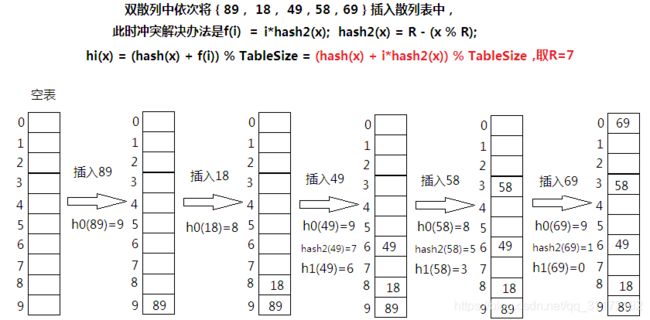
双散列：

注：

     1）探测散列表的删除是懒惰删除（只是简单的标记要删除的节点是为已删除DELETED,然后在查找等例程里面都人为的忽视标记过的节点. ），虽然这种情况下并不存在懒惰的意味；

     2）定理：如果使用平方探测，且表的大小是素数，那么当表至少有一半为空时，总能够插入一个新的元素【反证法】；

     3）如果双散列正确实现，预期的探测次数和随机冲突解决的情形相同，这使得双散列理论上很有吸引力。然而，平方探测不需要使用第二个散列函数，从而实践中可能更简单且快速，当键为字符串时其散列函数的计算将更加耗时；

 实例：建立开放定址法的散列表，完成插入、删除、再散列、查询、清除等功能。

1、 hash.h

//hash.h
#ifndef HASH_H_
#define HASH_H_

#include
#include
#include
#include
#include
#include
#include

using std::cout;
using std::endl;
using std::string;
using std::ostream;
using std::vector;
using std::list;
using std::setw;

class Student{
private:
	string name;
	string course;
	double score;
public:
	//Student constructor
	Student(const string &n, const string &c, double s):name(n), course(c), score(s){
	};
	//non parameter constructor
	Student():name(""), course(""), score(0.0){
	
	}
	
	//Student destructor
	~Student(){
	};
	
	//get name 
	const string & getName() const{
		return name;
	};
	
	//overload operator==
	bool operator==(const Student &stu) const{
		return name == stu.name;
	};
	
	//overload operator!=
	bool operator!=(const Student &stu) const{
		return !(*this == stu);
	};
	
	//overload operator<<
	friend ostream & operator<<(ostream &os, const Student &stu){
		cout << " name : " << stu.name << setw(8) << " course : " << setw(8) << stu.course << " score : " << stu.score << endl;
		return os;
	}	
};

//hash function
int hash(const string &key){
	int hashVal = 0;
	for(int i = 0; i < key.length(); i++){
		hashVal = 37 * hashVal + key[i];
	}
	
	return hashVal;
};

//overload hash function
int hash(const Student &stu){
	return hash(stu.getName());
};

template
class HashTable{
public:
	//define the EntryType 
	enum EntryType{ACTIVE, EMPTY, DELETED};
private:
	struct Entry{
		T element;
		EntryType info;
		//Entry constructor
		Entry(const T &obj = T(), EntryType i = EMPTY):element(obj), info(i){
		}
	};	
	
	vector table;
	int currentSize;
public:
	//HashTable constructor
	HashTable(int num = 7):table(nextPrime(num)), currentSize(0){
		makeEmpty();
	};
	
	//HashTable destructor
	~HashTable(){
	};
	
	//judge whether the table contain obj return T obj
	T findElement(const T &obj){
		int currentPos = findPos(obj);
		if(isActive(currentPos)){
			return table[currentPos].element;
		}else{
			T temp;
			return temp;
		}
	};
	
	//find the position of obj
	int findPos(const T &obj){
		/*
			linear prober : f(i) = i, delta = 1;
			square prober : f(i) = i * i, delte = 2 * i - 1;
			double hash : f(i) = i * hash2(x), 
						  hash2(x) = R - (x % R) whether R is prime and R < currentSize 
						  delta = hash2(x)
		*/
		int offSet = 1;
		int currentPos = myhash(obj);
		while((table[currentPos].info != EMPTY) && (table[currentPos].element != obj)){
			//linear prober currentPos += offSet;
			//square prober 
			//currentPos += 2 * offSet - 1;
			//double hash
			currentPos = prePrime(table.size()) - currentPos % prePrime(table.size());
			offSet++;
		}
		if(currentPos >= table.size()){
			currentPos -=  table.size();
		}
		return currentPos;
	};
	
	//judge whether table contain obj reutrn bool
	bool contain(const T &obj){
		return isActive(findPos(obj));
	};
	
	//empty the table
	void makeEmpty(){
		for(int i = 0; i < table.size(); i++){
			table[i].info = EMPTY;
		}
		currentSize = 0;
	};
	
	//judge whether table is empty
	bool isEmpty(){
		return currentSize == 0;
	};
	
	//insert obj into table
	bool insert(const T &obj){
		int currentPos = findPos(obj);
		if(isActive(currentPos)){
			return false;
		}
		table[currentPos] = Entry(obj, ACTIVE);
		if(++currentSize >= table.size() / 2){
			rehash();
		}
		return true;
	};
	
	//remove obj outof table
	bool remove(const T &obj){
		int currentPos = findPos(obj);
		if(!isActive(currentPos)){
			return false;
		}
		table[currentPos].info = DELETED;
		currentSize--;
		return true;
	};
	
	//print the table
	void print(){
		cout << " the table info as follows : " << endl;
		for(int i = 0; i < table.size(); i++){
			if(isActive(i)){
				cout << i << " : " << table[i] << endl;
			}
		}
	};
	
	friend ostream & operator<<(ostream &os, const Entry &e){
		os << "element : " << e.element << setw(8) << " info : " << e.info << endl;
		return os; 
	};
	
private:
	//rehash operation
	void rehash(){
		vector temp = table;
		table.resize(nextPrime(2 * table.size()));
		for(int i = 0; i < table.size(); i++){
			table[i].info = EMPTY;
		}
		currentSize = 0;
		for(int i = 0; i < temp.size(); i++){
			if(temp[i].info == ACTIVE){
				insert(temp[i].element);
			}
		}
	};
	
	//hash function
	int myhash(const T &obj) const{
		int hashVal = hash(obj);
		hashVal %= table.size();
		if(hashVal < 0){
			hashVal += table.size();
		}
		return hashVal;
	};
	
	//judge whether the obj at currentPos is actived or not 
	bool isActive(int currentPos) const{
		return table[currentPos].info == ACTIVE;
	};
	
	//find next prime which is bigger than currentSize
	int nextPrime(int n){
		//set flag
		bool flag = true;
		for(int i = n; ; i++) {
			for(int j = 2;j < i; j++) {
				if(i % j == 0) {
					//not a prime
					flag = false;
					break;
				}
			}
			//find the prime
			if(flag) {
				return i;
				break;
			}
			flag = true;
		}
	};
	
	//find previous prime which is smaller than currentSize
	int prePrime(int n){
		//set flag
		bool flag = true;
		for(int i = n; i > 1; i--) {
			for(int j = i - 1;j  > 1; j--) {
				if(i % j == 0) {
					//not a prime
					flag = false;
					break;
				}
			}
			//find the prime
			if(flag) {
				return i;
				break;
			}
			flag = true;
		}
	}; 
};

#endif

2、main.cpp

//main.cpp
#include
#include"hash.h"

using namespace std;

int main(){
	Student stu[6] = {
		Student("Aimi", "python", 80.6),
		Student("Brone", "C++", 90.3),
		Student("Cver", "python", 85.6),
		Student("David", "C++", 89.7),
		Student("Eular", "java", 85.0),
		Student("Frank", "C++", 92.1)
	};
	
	vector vstu;
	for(int i = 0; i < 6; i++){
		vstu.push_back(stu[i]);
	}
	
	for(int i = 0; i < 6; i++){
		cout << vstu[i];
	}
	
	cout << "******** insert ********" << endl;
	HashTable hashTable;
	for(int i = 0; i < 6; i++){
		hashTable.insert(vstu[i]);
	}
	
	cout << "******** print ********" << endl;
	hashTable.print();
	
	cout << "******** contain ********" << endl;	
	if(hashTable.contain(stu[0])){
		cout << " contain " << stu[0] << endl;
	}else{
		cout << "does not exist the object !" << endl;
	}
	
	cout << "******** findElement ********" << endl;
	cout << hashTable.findElement(stu[1]) << endl;
	
	cout << "******** insert ********" << endl;
	hashTable.insert(Student("Furier", "java", 89.0));
	hashTable.print();
	
	cout << "******** remove ********" << endl;	
	hashTable.remove(stu[3]);
	hashTable.print();	
	return 0;
}

practice makes perfect !

参考博客： 数据结构与算法——散列表类的C++实现(探测散列表)