【论文笔记】Continual Relation Learning via Episodic Memory Activation and Reconsolidation
Continual Relation Learning via Episodic Memory Activation and Reconsolidation
Abstract
持续关系学习:不遗忘以前关系的同时继续学习新关系
新关系的出现会忘记旧的关系,虽然有证明在新的关系训练序列中添加遗忘的训练样本可以避免这个问题,但是又容易陷入over-fitting
因此本文根据人类的长期记忆构成,设计了EMAR框架。
1 Introduction
-
OpenRE
-
ContinualRE
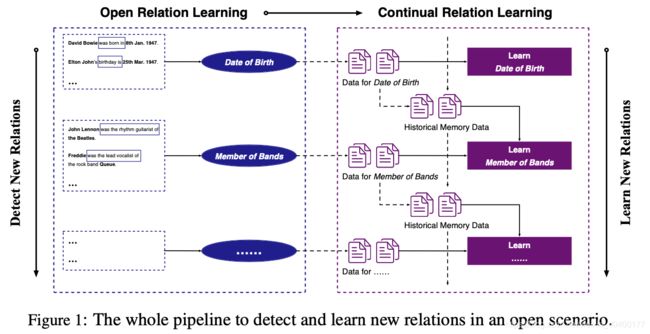
Continual RE最大的问题就是 灾难性遗忘,很难在学习新关系的同时避免忘记旧关系。这两个问题都是在开放场景下,pipeline是这样的:
memory-based方法,保留片段记忆,在继续训练新样本的过程中保留一部分以往的训练样本,是一个非常有效的解决灾难性遗忘的问题,但是这种方法依然不能解决过拟合的问题:
当模型在持续关系学习的环境下,会快速的改变以往关系的特征分布,逐渐过拟合于几个记忆中的样本,最终对旧的关系变得疑惑 (我认为这里似乎是想说停留的那一部分以往训练样本会过拟合。虽然不至于灾难性以往,但还是识别率下降了,瞧瞧,科研的话术多么的抽象)
这边有一段丢失了,不写了。包含related work和部分introduction(真烦死了
3 Methodogy
3.1 Task Definition and Overall Framework
持续关系学习在一个序列的任务上训练,每一个任务都有其训练集,验证集和测试集,Relation set。
任务要求模型在第 k k k个和前 k − 1 k-1 k−1个上都表现优异,模型会验证全部的测试集。因此,验证过程会越来越难。
片段记忆模块 M = { M 1 , M 2 , . . . } \mathcal{M}=\{\mathcal{M}_1, \mathcal{M}_2,...\} M={M1,M2,...}是一个集合,用于存储历史任务中的一些样例,每一个记忆模块 M k = { ( x 1 M k , y 1 M k ) , . . . , ( x B M k , y B M k ) } \mathcal{M}_k = \{(x_1^{\mathcal{M}_k}, y_1^{\mathcal{M}_k}),...,(x_B^{\mathcal{M}_k}, y_B^{\mathcal{M}_k})\} Mk={(x1Mk,y1Mk),...,(xBMk,yBMk)}
总之就是包含第 k k k个任务中的 B B B个训练样本。 B B B是constrained memory size。应该是一个比较有效的超参数,相同的情况下,记忆的越少,模型应该越有效果。
模型包含3个步骤来学习新关系并且避免遗忘:
- fine-tune encoder,让模型注意新关系的pattern
- 对于当前任务的关系集合中的每一个关系,都选去其中最有信息的样例(类似于prototype那种,存储在 M k \mathcal{M}_k Mk中。
- 迭代地采用记忆回放和激活,以及记忆再合并去学习新关系同时维持旧关系。
3.2 Example Encoder
BiLSTM,用于encode,额外添加了entity的开始和结束position。
3.3 Learning for New Tasks
对应模型fine tune于新任务的新关系,
L ( θ ) = − ∑ i = 1 N ∑ j = 1 ∣ R ~ k ∣ δ y i τ k = r j × log exp ( g ( f ( x i T k ) , r j ) ) ∑ l = 1 ∣ R ~ k ∣ exp ( g ( f ( x i T k ) , r l ) ) \begin{aligned} \mathcal{L}(\boldsymbol{\theta})=-\sum_{i=1}^{N} \sum_{j=1}^{\left|\tilde{\mathcal{R}}_{k}\right|} \delta_{y_{i}^{\tau_{k}}=r_{j}} \times \log \frac{\exp \left(g\left(f\left(x_{i}^{\mathcal{T}_{k}}\right), \boldsymbol{r}_{j}\right)\right)}{\sum_{l=1}^{\left|\tilde{\mathcal{R}}_{k}\right|} \exp \left(g\left(f\left(x_{i}^{\mathcal{T}_{k}}\right), \boldsymbol{r}_{l}\right)\right)} \end{aligned} L(θ)=−i=1∑Nj=1∑∣R~k∣δyiτk=rj×log∑l=1∣R~k∣exp(g(f(xiTk),rl))exp(g(f(xiTk),rj))
- r j \boldsymbol{r}_j rj是第 j j j个关系的embedding( r j ∈ R ~ k r_j \in \tilde{\mathcal{R}}_k rj∈R~k。注意 R ~ k \tilde{\mathcal{R}}_k R~k是在执行第 k k k个任务时,所有已知任务的关系合集(包含前面 k − 1 k-1 k−1个任务中的关系集合。
- g ( ⋅ , ⋅ ) g(\cdot, \cdot) g(⋅,⋅)时计算embedding相似度的。
- δ \delta δ时信号函数,当 y i T k = r j y_{i}^{\mathcal{T}_{k}}=r_{j} yiTk=rj 时成立,为1,其他为0
负对数似然函数嘛,其实就是希望当类别为 r j r_j rj的时刻,其encoder f ( x i T k ) f(x_i^{\mathcal{T}_k}) f(xiTk)的embedding与relation embedding r j \boldsymbol{r}_j rj 尽可能的接近(相似度为1)并且与其他relation embedding尽可能的相似度为0
对于每一个关系,会随机初始化relation embedding. i.e. r j \boldsymbol{r}_j rj
3.4 Selecting Examples for Memory
按照上面的整体步骤,对新任务fine tune了之后,要为 k + 1 k+1 k+1任务做准备了,留几个训练样例了要。因此选择 informative 和 diverse的examples。尽可能的覆盖这个任务中的关系模式。
在encoding第 k k k个任务中的examples之后,用K-Means去聚类,聚类中心个数就是上面所说的 B B B,对每一个聚类来说,选择最接近中心的样本。通过中心点的样本数量以及其本身的关系类别的数量,数量越多显现关系越重要。通过关系的重要程度来分配选择记录关系。
对于重要的关系,至少选取 ⌊ B ∣ R k ∣ ⌋ \left\lfloor\frac{B}{\left|\mathcal{R}_{k}\right|}\right\rfloor ⌊∣Rk∣B⌋ 个样本,对于不那么重要的,最多选取 ⌈ B ∣ R k ∣ ⌉ \left\lceil\frac{B}{\left|\mathcal{R}_{k}\right|}\right\rceil ⌈∣Rk∣B⌉个样本。
有趣的一点,如果任务样本小于 B B B,那么会填充其他关系的样例。(我猜是历史关系的样例
知道了每一个关系的选择数量之后,再次使用K-Means对类内样本进行聚类。中心数量由上面分配的数量决定的,尽可能选取接近中心点的。
3.5 Replay, Activation and Reconsolidation
最重要的第三步来了。
Computing Prototypes
通过结合所有的在片段记忆之中的样本,得到有完整的记忆 M ~ k = ⋃ i = 1 k M i \tilde{\mathcal{M}}_k=\bigcup_{i=1}^{k} \mathcal{M}_{i} M~k=⋃i=1kMi,然后从中对每一个关系 r i r_i ri,获取其全部的样例,把当前关系下的样例的encoded embedding平均一下,就得到了prototype embedding
p i = ∑ j = 1 ∣ P i ∣ f ( x j P i ) ∣ P i ∣ \boldsymbol{p}_{i}=\frac{\sum_{j=1}^{\left|\mathcal{P}_{i}\right|} f\left(x_{j}^{\mathcal{P}_{i}}\right)}{\left|\mathcal{P}_{i}\right|} pi=∣Pi∣∑j=1∣Pi∣f(xjPi)
Memory Replay and Activation
所有记忆中的样例 M ~ k \tilde{\mathcal{M}}_k M~k和第 k k k个任务的样例 T k \mathcal{T}_k Tk合并起来,得到 A k = M ~ k ∪ T k = { ( x 1 A k , y 1 A k ) , … , ( x M A k , y M A k ) } \mathcal{A}_{k}=\tilde{\mathcal{M}}_{k} \cup \mathcal{T}_{k}= \left\{\left(x_{1}^{\mathcal{A}_{k}}, y_{1}^{\mathcal{A}_{k}}\right), \ldots,\left(x_{M}^{\mathcal{A}_{k}}, y_{M}^{\mathcal{A}_{k}}\right)\right\} Ak=M~k∪Tk={(x1Ak,y1Ak),…,(xMAk,yMAk)}
持续的激活模型去学习新关系和记住就关系。损失函数为:
L A ( θ ) = − ∑ i = 1 M ∑ j = 1 ∣ R ~ k ∣ δ y i A k = r j × log exp ( g ( f ( x i A k ) , r j ) ) ∑ l = 1 ∣ R ~ k ∣ exp ( g ( f ( x i A k ) , r l ) ) \begin{aligned} \mathcal{L}^{\mathcal{A}}(\boldsymbol{\theta})=-\sum_{i=1}^{M} \sum_{j=1}^{\left|\tilde{\mathcal{R}}_{k}\right|} \delta_{y_{i}^{\mathcal{A}_{k}}=r_{j}} \times \log \frac{\exp \left(g\left(f\left(x_{i}^{\mathcal{A}_{k}}\right), \boldsymbol{r}_{j}\right)\right)}{\sum_{l=1}^{\left|\tilde{\mathcal{R}}_{k}\right|} \exp \left(g\left(f\left(x_{i}^{\mathcal{A}_{k}}\right), \boldsymbol{r}_{l}\right)\right)} \end{aligned} LA(θ)=−i=1∑Mj=1∑∣R~k∣δyiAk=rj×log∑l=1∣R~k∣exp(g(f(xiAk),rl))exp(g(f(xiAk),rj))
其实没什么变化,就是训练集合引入了之前记忆中的一些关系。
Memory Reconsolidation
文章主要的重点应该是在此处,reconsolidation
对于每一个已知的关系 r i ∈ R ~ k r_i \in \tilde{\mathcal{R}}_k ri∈R~k,采样它的样例集合,其中每一个样本也都是来源于 M ~ k \tilde{\mathcal{M}}_k M~k。
L R ( θ ) = − ∑ i = 1 ∣ R ~ k ∣ ∑ j = 1 ∣ I i ∣ log exp ( g ( f ( x j I i ) , p i ) ) ∑ l = 1 ∣ R ~ k ∣ exp ( g ( f ( x j I i ) , p l ) ) \begin{aligned} \mathcal{L}^{\mathcal{R}}(\boldsymbol{\theta}) &=-\sum_{i=1}^{\left|\tilde{\mathcal{R}}_{k}\right|} \sum_{j=1}^{\left|\mathcal{I}_{i}\right|} \\ \log & \frac{\exp \left(g\left(f\left(x_{j}^{\mathcal{I}_{i}}\right), \boldsymbol{p}_{i}\right)\right)}{\sum_{l=1}^{\left|\tilde{\mathcal{R}}_{k}\right|} \exp \left(g\left(f\left(x_{j}^{\mathcal{I}_{i}}\right), \boldsymbol{p}_{l}\right)\right)} \end{aligned} LR(θ)log=−i=1∑∣R~k∣j=1∑∣Ii∣∑l=1∣R~k∣exp(g(f(xjIi),pl))exp(g(f(xjIi),pi))
其中 p l \boldsymbol{p}_l pl是 prototype embedding。通过上面的公式计算出来的
3.6 Training and Prediction
对于第 k k k个任务,首先使用 L ( θ ) \mathcal{L}(\boldsymbol{\theta}) L(θ) 优化几个epoch。
然后迭代优化 L A ( θ ) \mathcal{L}^{\mathcal{A}}(\boldsymbol{\theta}) LA(θ)和 L B ( θ ) \mathcal{L}^{\mathcal{B}}(\boldsymbol{\theta}) LB(θ) 直到拟合
这就牛了,由于文章的核心思想,其实主要就是想突出在片段记忆的时刻,对人脑来说,记忆很容易被修改和删除。但是通过这样采样迭代训练的方式,让之前的relation和现在的relation都达到一个比较稳定的状态,难怪作者会说stable的情况下开始下一个任务。
在完成第 k k k个任务之后,对于每一个关系,抽取出一个样例数量为 S S S的集合称为 E i \mathcal{E}_i Ei,计算最终的关系prototype如下:
p ~ i = r i + ∑ j = 1 S f ( x j E i ) 1 + S \tilde{\boldsymbol{p}}_{i}=\frac{\boldsymbol{r}_{i}+\sum_{j=1}^{S} f\left(x_{j}^{\mathcal{E}_{i}}\right)}{1+S} p~i=1+Sri+∑j=1Sf(xjEi)
所以在最终的预测中,只需要将instance放进来,和prototype的关系进行对比就可以了。
结果可以看下表:
4 Experiments
Datasets and Experimental Settings
文章一共准备了三个数据集
-
FewRel: 80个关系分成10个task (自家出品,稳定涨引用)
-
SimpleQuestions: knowledge base 数据集 分成了20个task
-
TACRED: 42中关系分成10中数据集。其中删除掉了n/a 类型的关系
Average Performance可以看到 EMAR在随着任务增加的情况下,性能还是比较稳定的,那个紫色的叫EWC,大家做实验的时候,一定要带上它。
这边设计的比较巧妙,比较了:
- whole performance,就是经过了所有的task之后最终的evaluation。
- average performance,就是平均了所有看见过的task的性能。这一个方法会严重的突出遗忘的问题。
任务的顺序这些也会影响性能,所有作者用了相当多一样的setting来使得对照非常的公平,大部分都参照了 continual relation learning的第一篇文章:
Sentence Embedding Alignment for Lifelong Relation Extraction
Effect of Memory Size
表格结果如下:
记忆单元的增加有效的提升模型性能
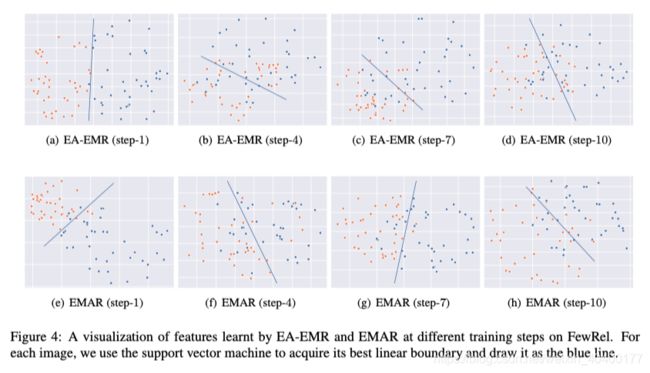
Effect of Prototypes and Reconsolidation
这一部分主要强调了学的prototype和feature非常有用,使用SVM决策效果更好。图与表格如下