POJ 1625 Censored!（AC自动机+dp+高精度）

Censored! Time Limit: 5000MS   Memory Limit: 10000K Total Submissions: 10864   Accepted: 2978 Description The alphabet of Freeland consists of exactly N letters. Each sentence of Freeland language (also known as Freish) consists of exactly M letters without word breaks. So, there exist exactly N^M different Freish sentences. But after recent election of Mr. Grass Jr. as Freeland president some words offending him were declared unprintable and all sentences containing at least one of them were forbidden. The sentence S contains a word W if W is a substring of S i.e. exists such k >= 1 that S[k] = W[1], S[k+1] = W[2], ...,S[k+len(W)-1] = W[len(W)], where k+len(W)-1 <= M and len(W) denotes length of W. Everyone who uses a forbidden sentence is to be put to jail for 10 years. Find out how many different sentences can be used now by freelanders without risk to be put to jail for using it. Input The first line of the input file contains three integer numbers: N -- the number of letters in Freish alphabet, M -- the length of all Freish sentences and P -- the number of forbidden words (1 <= N <= 50, 1 <= M <= 50, 0 <= P <= 10). The second line contains exactly N different characters -- the letters of the Freish alphabet (all with ASCII code greater than 32). The following P lines contain forbidden words, each not longer than min(M, 10) characters, all containing only letters of Freish alphabet. Output Output the only integer number -- the number of different sentences freelanders can safely use. Sample Input 2 3 1 ab bb Sample Output 5 Source Northeastern Europe 2001, Northern Subregion

        大致题意，给你n个字符，和一个长度m，所有的单词都由m个这些字符构成，于是总的单词数目为n^m。然后再给你一些单词（长度不一定是m），所有包含这些单词的单词都不算是合法的单词，现在问你总共有多少个合法的单词。

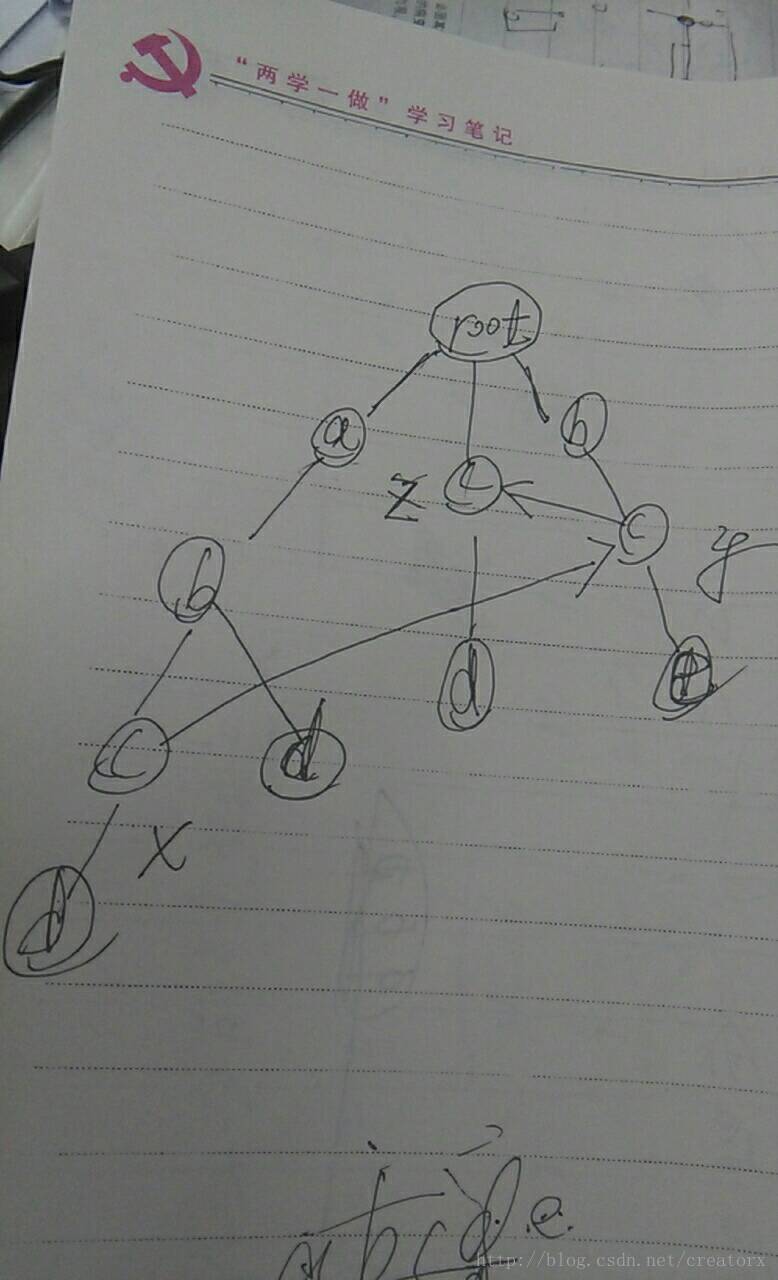
        这种题目用dp的话还是挺明显的，但是普通的dp并不能够判断是否已经构成了合法单词，缺少判断的手段。于是只能借助于AC自动机。我们把所有给出的不合法单词构造AC自动机，当然要注意的是，对于fail指针，我们得做出一些修改。在Trie中，如果一个节点x无法到达字母a，但是它的fail能够到达a，那么我们要连边x到它fail的a。然后有状态转移方程dp[i][x]=dp[i][x]+dp[i-1][y]，其中x是y的后继节点。具体来说，我们还是可以拿之前那个图来说说。

                 

        比如说到了左边的c点，然后我要找e，发现没有，于是通过fail指针到了右边的c下面那个e，相当于长度增加了一个e，然后在判断不合法的时候舍弃了前面的a。这样一来，我们在累加的时候，首先判断那个点是否为AC自动机中的单词结尾的关键点，如果不是那么可以累加，否则不累加。然后，我们再说说AC自动机中没有出现的字符，比如所在这个图中，我没有z，那么是在可选字符中有z，我们当然要考虑这个z的影响。AC自动机中没有z，那么便是空指针，指向root，于是所有的，以这类字符结尾的合法串的数目就都统计到root节点中去了，并不会影响最后的结果，而且恰好符合这个dp的过程。最后结果就是每一个非单词结尾节点的方案数之和。

        然后此题数据还比较大，需要用到高精度，由于仅仅只是加法，所以就用c++来写了。具体见代码：

#include 
#include 
#include 
#include 
#include 
#include 
#define INF 0x3f3f3f3f
#define LL long long
#define N 110

using namespace std;

int h[256];

struct AC_automation
{
    struct node{int fail,cnt,ch[N];}T[N];
    int tot,root;

    void init()
    {
        tot=root=0;
        memset(T,0,sizeof(T));
    }

    void ins(unsigned char* x)
    {
        int o=root;
        for(int k=0;x[k];k++)
        {
            int c=h[x[k]];
            if(!T[o].ch[c]) T[o].ch[c]=++tot;
            o=T[o].ch[c];
        }
        T[o].cnt++;
    }

    void get_fail()
    {
        queue q;
        q.push(root);
        while(!q.empty())
        {
            int o=q.front();
            T[o].cnt=T[o].cnt|T[T[o].fail].cnt;
            for(int i=0;i<100;i++)
            {
                if (!T[o].ch[i])
                {
                    T[o].ch[i]=T[T[o].fail].ch[i];
                    continue;
                }
                if (o!=root)
                {
                    int fa=T[o].fail;
                    while(fa&&!T[fa].ch[i]) fa=T[fa].fail;
                    T[T[o].ch[i]].fail=T[fa].ch[i];
                } else T[T[o].ch[i]].fail=root;
                q.push(T[o].ch[i]);
            } q.pop();
        }
    }

} AC;

struct BigInteger
{
    int A[25];
    enum{MOD = 10000};
    BigInteger(){memset(A,0,sizeof(A)); A[0]=1;}
    void Set(int x){memset(A,0,sizeof(A)); A[0]=1; A[1]=x;}

    void print()
    {
        printf("%d",A[A[0]]);
        for (int i=A[0]-1;i>0;i--)
        {
            if (A[i]==0){printf("0000"); continue;}
            for (int k=10;k*A[i]0) C[0]++;
        return C;
    }

    BigInteger operator * (const BigInteger& B)
    {
        BigInteger C;
        C[0]=A[0]+B[0];
        for (int i=1;i<=A[0];i++)
            for (int j=1;j<=B[0];j++)
                C[i+j-1]+=A[i]*B[j],C[i+j]+=C[i+j-1]/MOD,C[i+j-1]%=MOD;
        if (C[C[0]]==0) C[0]--;
        return C;
    }

};

int main()
{
    int n,m,p;
    while(~scanf("%d%d%d",&n,&m,&p))
    {
        AC.init();
        unsigned char s[100];
        scanf("%s",s);
        for(int i=0;i

        现在回过头来看AC自动机上的dp，其实无非就是在AC自动机上面做dp，与树形dp类似，AC自动机提供了一个dp的大体方向和转移的顺序。与此同时，由于其记录单词的特殊性，所以对于一些连续性的检测统计起来也很方便。