树状数组总结(转)
转载链接:传送门
目录:
① 单点修改、区间查询 树状数组
原理
② 区间查询、单点修改 树状数组
③ 区间查询、区间修改 树状数组
④ 二维树状数组
单点修改、区间查询 二维树状数组
区间修改、单点查询 二维树状数组
区间修改、区间查询 二维树状数组
①单点修改、区间查询BIT:
首先当然是最基础的树状数组了,单点修改、区间查询的树状数组代码:
//BIT - 单点增加,区间查询 - st
struct _BIT{
int N,C[MAXN];
int lowbit(int x){return x&(-x);}
void init(int n)//初始化共有n个点
{
N=n;
for(int i=1;i<=N;i++) C[i]=0;
}
void add(int pos,int val)//在pos点加上val
{
while(pos<=N)
{
C[pos]+=val;
pos+=lowbit(pos);
}
}
int sum(int pos)//查询1~pos点的和
{
int ret=0;
while(pos>0)
{
ret+=C[pos];
pos-=lowbit(pos);
}
return ret;
}
}BIT;
//BIT - 单点增加,区间查询 - ed
原理:
假设我们现在要维护的是a数组,我们实际存储的是c数组,他们两者的关系如图:
有:
C1 = A1
C2 = A1+A2
C3 = A3
C4 = A1+A2+A3+A4
C5 = A5
C6 = A5+A6
C7 = A7
C8 = A1+A2+A3+A4+A5+A6+A7+A8c[i]不再是简单的存储a[i],而是存储了a[i]+a[i-1]+…+a[k],它存储了从a[i]往前若干个元素的和,那么如何确定k呢?这就关系到lowbit函数……
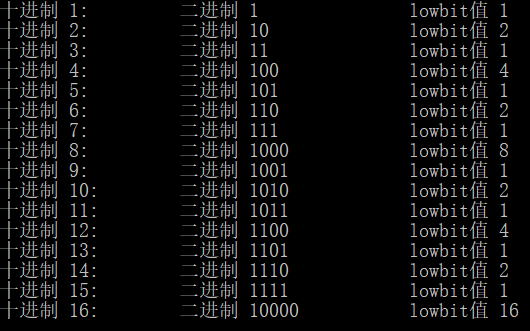
lowbit(x)函数返回的是什么?先看下图:
不难看出,lowbit(x)返回的是:若二进制下数字 xx 的尾部的零的个数为 k ,则lowbit(x) = 2k2k;
也就是说,c数组中,
若i为奇数,c[i]=a[i]c[i]=a[i];
若i为偶数,而其最多能整除k次2,c[i]=a[i]+a[i−1]+⋯+a[i−2k+1]c[i]=a[i]+a[i−1]+⋯+a[i−2k+1];
这样一来,对于某个pos点的增加xx,只要不断令pos+=lowbit(pos),就相当于一直往父亲节点走,所以我们在每个父亲节点都要增加xx。
②区间修改、单点查询BIT:
其实这个的原理就是:通过差分把这个区间修改、单点查询的问题转化为①;
首先,假设我们要记录的数组是a[1:n]a[1:n],那么我们假设有d[i]=a[i]−a[i−1]d[i]=a[i]−a[i−1],且d[1]=a[1]d[1]=a[1],
显然,就有a[i]=d[1]+d[2]+⋯+d[i]a[i]=d[1]+d[2]+⋯+d[i],
我们在BIT中实际存储的是数组d[1:n]d[1:n](准确的说是d数组的树状数组);
先说修改:
我们目标是给a[L:R]a[L:R]全部加上xx,那么我们不难发现,其实d[L+1],d[L+2],⋯,d[R]d[L+1],d[L+2],⋯,d[R]都没有变化,
而变化的只有:d[L]d[L]增加了xx,d[R+1]d[R+1]减少了xx;
所以只需要add(L,x),add(R+1,-x)即可。
再说查询:
我们要单点查询a[pos]a[pos],由上可知a[pos]=d[1]+d[2]+⋯+d[pos]a[pos]=d[1]+d[2]+⋯+d[pos],
那么原来的sum(pos)函数不用修改,就正好能返回a[pos]a[pos]的值。
代码:
//BIT - 区间修改,单点查询 - st
struct _BIT{
int N,C[MAXN];
int lowbit(int x){return x&(-x);}
void init(int n)//初始化共有n个点
{
N=n;
for(int i=1;i<=N;i++) C[i]=0;
}
void add(int pos,int val)
{
while(pos<=N) C[pos]+=val,pos+=lowbit(pos);
}
void range_add(int l,int r,int x)//区间[l,r]加x
{
add(l,x);
add(r+1,-x);
}
int ask(int pos)//查询pos点的值
{
int ret=0;
while(pos>0)
{
ret+=C[pos];
pos-=lowbit(pos);
}
return ret;
}
}BIT;
//BIT - 区间修改,单点查询 - ed③区间修改,区间查询BIT:
这个就很骚气了,这样的BIT可以很轻松地应付线段树模板题。
我们看到,由于我们目标记录的是数组a[1:n]a[1:n],而实际存储的是d[1:n]d[1:n],
那么已经实现了区间修改,如何完成区间查询呢?显然,区间查询的基础是快速求数组a[1:n]a[1:n]的前缀和,
显然数组a[1:n]a[1:n]的前缀和:
a[1]+a[2]+⋯+a[i]=d[1]×i+d[2]×(i−1)+⋯+d[i]×1a[1]+a[2]+⋯+a[i]=d[1]×i+d[2]×(i−1)+⋯+d[i]×1
不难发现右侧可以化成:
d[1]×i+d[2]×(i−1)+⋯+d[i]×1=[d[1]×(i+1)+d[2]×(i+1)+⋯+d[i]×(i+1)]−[d[1]×1+d[2]×2+⋯+d[i]×i]=(i+1)×(d[1]+d[2]+⋯+d[i])−(d[1]×1+d[2]×2+⋯+d[i]×i)d[1]×i+d[2]×(i−1)+⋯+d[i]×1=[d[1]×(i+1)+d[2]×(i+1)+⋯+d[i]×(i+1)]−[d[1]×1+d[2]×2+⋯+d[i]×i]=(i+1)×(d[1]+d[2]+⋯+d[i])−(d[1]×1+d[2]×2+⋯+d[i]×i)
这样一来,我们就可以想到,在原来的数组C[i]C[i]记录d[i]d[i]的基础上,
再搞一个数组C2[i]C2[i]记录d[i]×id[i]×i即可。(当然,实际写代码的时候要明确,C数组和C2数组都是树状数组,不是原数组)
代码:
//BIT - 区间修改,区间查询 - st
struct _BIT{
int N;
ll C[MAXN],C2[MAXN];//分别记录d[i]和d[i]*i
int lowbit(int x){return x&(-x);}
void init(int n)//初始化共有n个点
{
N=n;
memset(C,0,sizeof(C));
memset(C2,0,sizeof(C2));
}
void add(int pos,ll val)
{
for(int i=pos;i<=N;i+=lowbit(i)) C[i]+=val,C2[i]+=val*pos;
}
void range_add(int l,int r,ll x)//区间[l,r]加上x
{
add(l,x);
add(r+1,-x);
}
ll ask(int pos)
{
ll ret=0;
for(int i=pos;i>0;i-=lowbit(i)) ret+=(pos+1)*C[i]-C2[i];
return ret;
}
ll range_ask(int l,int r)//查询区间[l,r]的和
{
return ask(r)-ask(l-1);
}
}BIT;
//BIT - 区间修改,区间查询 - ed
④二维树状数组:
在一维树状数组中,数组C[x]记录了的是右端点为x、长度为lowbit(x)的区间的区间和(具体参见原理)。
那么我们也可以类似地定义C[x][y]记录的是右下角为(x,y),高为 lowbit(x),宽为 lowbit(y) 的区间的区间和。
这就是二维树状数组最基本的原理。
④-①单点修改、区间查询 二维树状数组:
对于一维的树状数组稍加修改,就能得到:
#include
using namespace std;
typedef long long ll;
const int maxn=1005;
const int maxm=1005;
struct BIT_2D
{
int n,m;
ll C[maxn][maxm];
int lowbit(int x){return x&(-x);}
void init(int n,int m) //初始化n行m列矩阵
{
this->n=n;
this->m=m;
memset(C,0,sizeof(C));
}
void add(int x,int y,ll val) //在点(x,y)加上val
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j)) C[i][j]+=val;
}
ll ask(int x,int y) //求左上角为(1,1)右下角为(x,y)的矩阵和
{
ll ret=0;
for(int i=x;i>0;i-=lowbit(i))
for(int j=y;j>0;j-=lowbit(j)) ret+=C[i][j];
return ret;
}
}BIT;
int main()
{
int n=10,m=10;
BIT.init(n,m);
BIT.add(1,1,2);
BIT.add(3,6,7);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++) cout< ④-②区间修改、单点查询 二维树状数组:
和之前的一维树状数组一样,仿照②区间查询、单点修改树状数组的操作,同样用差分的方法,将本问题转化为④-①,
由于数组a[i][j]a[i][j]的前缀和有这样的公式:
sum[i][j]=(sum[i−1][j]+sum[i][j−1]−sum[i−1][j−1])+a[i][j]sum[i][j]=(sum[i−1][j]+sum[i][j−1]−sum[i−1][j−1])+a[i][j]
套用求前缀和的形式,假设差分数组为d[i][j]d[i][j],可以有:
a[i][j]=(a[i−1][j]+a[i][j−1]−a[i−1][j−1])+d[i][j]a[i][j]=(a[i−1][j]+a[i][j−1]−a[i−1][j−1])+d[i][j]
就能得到:
d[i][j]=a[i][j]−(a[i−1][j]+a[i][j−1]−a[i−1][j−1])d[i][j]=a[i][j]−(a[i−1][j]+a[i][j−1]−a[i−1][j−1])
那么,同样先说修改:
目标是给(x1,y1)(x1,y1)到(x2,y2)(x2,y2)的矩阵全部加上xx,不难发现,差分数组变动的只有四个点:
d[x1][y1]+=x,d[x1][y2+1]−=x,d[x2+1][y1]−=x,d[x2+1][y2+1]+=xd[x1][y1]+=x,d[x1][y2+1]−=x,d[x2+1][y1]−=x,d[x2+1][y2+1]+=x
这个可以自己举个栗子验证一下。
再说查询:
同一维树状数组一样,求左上角为(1,1)(1,1)右下角为(x,y)(x,y)的矩阵和就是d[x][y]的前缀和,正好就是要查询的a[x][y]。
代码:
#include
using namespace std;
typedef long long ll;
const int maxn=1005;
const int maxm=1005;
struct BIT_2D
{
int n,m;
ll C[maxn][maxm];
int lowbit(int x){return x&(-x);}
void init(int n,int m) //初始化n行m列矩阵
{
this->n=n;
this->m=m;
memset(C,0,sizeof(C));
}
void add(int x,int y,ll val)
{
for(int i=x;i<=n;i+=lowbit(i))
for(int j=y;j<=m;j+=lowbit(j)) C[i][j]+=val;
}
void range_add(int x1,int y1,int x2,int y2,ll x) //左上角为(x1,y1)右下角为(x2,y2)的矩阵全部加上x
{
add(x1,y1,x);
add(x1,y2+1,-x);
add(x2+1,y1,-x);
add(x2+1,y2+1,x);
}
ll ask(int x,int y) //查询点(x,y)的值
{
ll ret=0;
for(int i=x;i>0;i-=lowbit(i))
for(int j=y;j>0;j-=lowbit(j)) ret+=C[i][j];
return ret;
}
}BIT;
int main()
{
int n=10,m=10;
BIT.init(n,m);
BIT.range_add(2,2,4,4,1);
BIT.range_add(5,6,8,8,2);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++) cout< ④-②区间修改、区间查询 二维树状数组:
又到了最亦可赛艇的部分了!依然仿照③区间查询、区间修改 树状数组的操作。
首先sum[i][j]=∑x=1i∑y=1ja[x][y]sum[i][j]=∑x=1i∑y=1ja[x][y],
又由于a[x][y]=∑u=1x∑v=1yd[u][v]a[x][y]=∑u=1x∑v=1yd[u][v],
所以有:
sum[i][j]=∑x=1i∑y=1j(∑u=1x∑v=1yd[u][v])sum[i][j]=∑x=1i∑y=1j(∑u=1x∑v=1yd[u][v])
可以说是非常复杂了……
但模仿③的操作,我们依然可以统计d[u][v]出现次数:
不难想象,从a[1][1]a[1][1]到a[i][j]a[i][j],d[1][1]d[1][1]全部都要出现一次,所以有i×ji×j个d[1][1]d[1][1],即d[1][1]×i×jd[1][1]×i×j
类似的,有d[1][2]×i×(j−1),d[2][1]×(i−1)×j,d[2][2]×(i−1)×(j−1)d[1][2]×i×(j−1),d[2][1]×(i−1)×j,d[2][2]×(i−1)×(j−1) 等等等等……
所以我们不难把式子变成:
sum[i][j]=∑x=1i∑y=1j[d[x][y]×(i+1−x)×(j+1−y)]sum[i][j]=∑x=1i∑y=1j[d[x][y]×(i+1−x)×(j+1−y)]
展开得到:
sum[i][j]=∑x=1i∑y=1j[d[x][y]⋅(i+1)(j+1)−d[x][y]⋅x(j+1)−d[x][y]⋅(i+1)y+d[x][y]⋅xy]sum[i][j]=∑x=1i∑y=1j[d[x][y]⋅(i+1)(j+1)−d[x][y]⋅x(j+1)−d[x][y]⋅(i+1)y+d[x][y]⋅xy]
也就相当于把这个式子拆成了四个部分:
(i+1)(j+1)×∑x=1i∑y=1jd[x][y]−(j+1)×∑x=1i∑y=1j(d[x][y]⋅x)−(i+1)×∑x=1i∑y=1j(d[x][y]⋅y)∑x=1i∑y=1j(d[x][y]⋅xy)(i+1)(j+1)×∑x=1i∑y=1jd[x][y]−(j+1)×∑x=1i∑y=1j(d[x][y]⋅x)−(i+1)×∑x=1i∑y=1j(d[x][y]⋅y)∑x=1i∑y=1j(d[x][y]⋅xy)
所以我们需要在原来 C1[i][j]C1[i][j] 记录 d[i][j]d[i][j] 的基础上,再添加三个树状数组:
C2[i][j]C2[i][j] 记录 d[i][j]⋅id[i][j]⋅i
C3[i][j]C3[i][j] 记录 d[i][j]⋅jd[i][j]⋅j
C4[i][j]C4[i][j] 记录 d[i][j]⋅ijd[i][j]⋅ij
这样一来,就能通过数组a[i][j]a[i][j]的差分数组d[i][j]d[i][j]来得到a[i][j]a[i][j]的前缀和数组sum[i][j]sum[i][j],
最后,易知(x1,y1)(x1,y1)到(x2,y2)(x2,y2)的矩阵和就等于sum[x2][y2]−sum[x2][y1−1]−sum[x1−1][y2]+sum[x1−1][y1−1]sum[x2][y2]−sum[x2][y1−1]−sum[x1−1][y2]+sum[x1−1][y1−1]。
代码:
#include
using namespace std;
typedef long long ll;
const int maxn=1005;
const int maxm=1005;
struct BIT_2D
{
int n,m;
ll C1[maxn][maxm],C2[maxn][maxm],C3[maxn][maxm],C4[maxn][maxm];
int lowbit(int x){return x&(-x);}
void init(int n,int m) //初始化n行m列矩阵
{
this->n=n;
this->m=m;
memset(C1,0,sizeof(C1));
memset(C2,0,sizeof(C2));
memset(C3,0,sizeof(C3));
memset(C4,0,sizeof(C4));
}
void add(int x,int y,ll val)
{
for(int i=x;i<=n;i+=lowbit(i))
{
for(int j=y;j<=m;j+=lowbit(j))
{
C1[i][j]+=val;
C2[i][j]+=val*x;
C3[i][j]+=val*y;
C4[i][j]+=val*x*y;
}
}
}
void range_add(int x1,int y1,int x2,int y2,ll x) //左上角为(x1,y1)右下角为(x2,y2)的矩阵全部加上x
{
add(x1,y1,x);
add(x1,y2+1,-x);
add(x2+1,y1,-x);
add(x2+1,y2+1,x);
}
ll ask(int x,int y) //查询左上角为(1,1)右下角为(x,y)的矩阵和
{
ll ret=0;
for(int i=x;i>0;i-=lowbit(i))
{
for(int j=y;j>0;j-=lowbit(j))
{
ret+=(x+1)*(y+1)*C1[i][j];
ret-=(y+1)*C2[i][j]+(x+1)*C3[i][j];
ret+=C4[i][j];
}
}
return ret;
}
ll range_ask(int x1,int y1,int x2,int y2) //查询左上角为(x1,y1)右下角为(x2,y2)的矩阵和
{
return ask(x2,y2)-ask(x1-1,y2)-ask(x2,y1-1)+ask(x1-1,y1-1);
}
}BIT;
int main()
{
int n=10,m=10;
BIT.init(n,m);
BIT.range_add(2,2,4,4,1);
BIT.range_add(5,6,8,8,2);
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++) cout<