牛客 - sequence(笛卡尔树+线段树)

题目链接：点击查看

题目大意：给出一个长度为 n 的数列 a 和数列 b ，求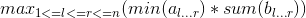

题目分析：不算难的题目，对于每个 a[ i ] 求一下贡献然后维护最大值就好，具体思路就是，先找出每个 a[ i ] 左右两侧分别小于 a[ i ] 的位置，分别记为 l 和 r，再对数列 b 维护一下前缀和 sum，比较显然的就是 ( l , r ) 这段区间内，凡是跨过位置 i 的区间最小值一定是 a[ i ]，然后分类讨论一下：

1. 如果 a[ i ] > 0：在 [ l - 1 , i - 1 ] 中找到 sum 的最小值，在 [ i , r ] 中找到 sum 的最大值，贡献为 a[ i ] * ( mmax - mmin )
2. 如果 a[ i ] < 0：在 [ l - 1 , i - 1 ] 中找到 sum 的最大值，在 [ i , r ] 中找到 sum 的最小值，贡献为 a[ i ] * ( mmin - mmax )

区间最大值可以用 st 表或者线段树来维护，现在的问题就是如何快速找到每个 a[ i ] 的 l 和 r，用单调栈 O( n ) 扫一遍显然是没问题的，但为了练习笛卡尔树，可以利用笛卡尔树的性质，O( n ) 无脑建树后，dfs 扫一遍每个节点计算贡献也是一样的

代码：
 

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include