入门者笔记·Dijkstra与SPFA

Dijkstra

Dijkstra主要处理无负环（环上各条边的权值之和为负）的连通图，时间复杂度为n*n，有STL的优化方法可以减少时间复杂度。
其主要思想为每次寻找距离出发点最近且未被遍历的点，并对其进行松弛处理。

例题：P1339 [USACO09OCT]热浪Heat Wave

原题地址

题目描述

The good folks in Texas are having a heatwave this summer. Their Texas Longhorn cows make for good eating but are not so adept at creating creamy delicious dairy products. Farmer John is leading the charge to deliver plenty of ice cold nutritious milk to Texas so the Texans will not suffer the heat too much.

FJ has studied the routes that can be used to move milk from Wisconsin to Texas. These routes have a total of T (1 <= T <= 2,500) towns conveniently numbered 1…T along the way (including the starting and ending towns). Each town (except the source and destination towns) is connected to at least two other towns by bidirectional roads that have some cost of traversal (owing to gasoline consumption, tolls, etc.). Consider this map of seven towns; town 5 is the

source of the milk and town 4 is its destination (bracketed integers represent costs to traverse the route):

                          [1]----1---[3]-
                         /               \
                  [3]---6---[4]---3--[3]--4
                 /               /       /|
                5         --[3]--  --[2]- |
                 \       /        /       |
                  [5]---7---[2]--2---[3]---
                        |       /
                       [1]------

Traversing 5-6-3-4 requires spending 3 (5->6) + 4 (6->3) + 3 (3->4) = 10 total expenses.

Given a map of all the C (1 <= C <= 6,200) connections (described as two endpoints R1i and R2i (1 <= R1i <= T; 1 <= R2i <= T) and costs (1 <= Ci <= 1,000), find the smallest total expense to traverse from the starting town Ts (1 <= Ts <= T) to the destination town Te (1 <= Te <= T).

输入输出格式

输入格式：
第一行: 4个由空格隔开的整数: T, C, Ts, Te

第2到第C+1行: 第i+1行描述第i条道路。有3个由空格隔开的整数: Rs, Re和Ci

输出格式：
一个单独的整数表示从Ts到Te的最小总费用。数据保证至少存在一条道路。

输入输出样例

输入样例#1：
7 11 5 4
2 4 2
1 4 3
7 2 2
3 4 3
5 7 5
7 3 3
6 1 1
6 3 4
2 4 3
5 6 3
7 2 1
输出样例#1：
7
说明

【样例说明】
5->6->1->4 (3 + 1 + 3)

代码：

#include 
#include
#include
#include
#include
#include
#include
using namespace std;
int di[10010],book[10010];
int n,m,a,b;
struct node
{
    int r,dis;
}t;
vector<node>ww[10010];
void dijk(int x)
{
    int i,j,mi,t;
    for(i=0;i<ww[x].size();i++)
        di[ww[x][i].r]=min(di[ww[x][i].r],ww[x][i].dis);
    for(i=1;i<=n-1;i++)
    {
        int mi=1e9;
        for(j=1;j<=n;j++)
        {
            if(di[j]<mi&&!book[j])
            {
                mi=di[j];
                t=j;
            }
        }
        book[t]=1;
        for(j=0;j<ww[t].size();j++)
            if(!book[ww[t][j].r]) di[ww[t][j].r]=min(di[ww[t][j].r],di[t]+ww[t][j].dis);//松弛处理
    }
}
int main()
{
    int i,c,d,e;
    scanf("%d%d%d%d",&n,&m,&a,&b);
    for(i=1;i<=m;i++)
    {
        scanf("%d%d%d",&c,&d,&e);
        t.r=d;
        t.dis=e;
        ww[c].push_back(t);
        t.r=c;
        ww[d].push_back(t);
    }
    memset(book,0,sizeof(book));
    for(i=1;i<=n;i++)
        di[i]=1e9;
    di[a]=0;
    dijk(a);
    printf("%d\n",di[b]);
    return 0;
}

SPFA

主要处理有负环的连通图，可先用BFS或DFS判断是否有负环，易被各种变态数据卡，详情可百度“卡SPFA”（可怜我小破交好容易发明一个算法，还被各种丧心病狂的出题人针对）。
时间复杂度为m，但SPFA算法稳定性较差，在稠密图中SPFA算法时间复杂度会退化，比方说：

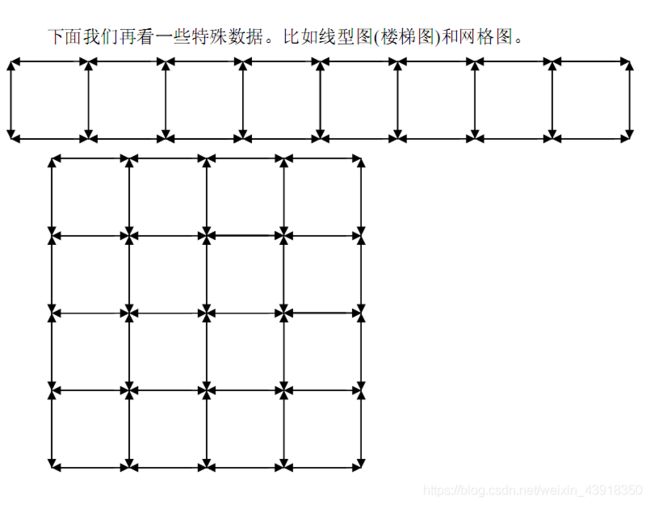
主要思想为每次对于一个路径，判断其是否可以松弛，如果可以，将其列入队列，再依次判断与队列中点相连的点与路径。
过程演示：
详细讲解

例题：P1396 营救

原题地址

题目描述

“咚咚咚……”“查水表！”原来是查水表来了，现在哪里找这么热心上门的查表员啊！小明感动的热泪盈眶，开起了门……

妈妈下班回家，街坊邻居说小明被一群陌生人强行押上了警车！妈妈丰富的经验告诉她小明被带到了t区，而自己在s区。

该市有m条大道连接n个区，一条大道将两个区相连接，每个大道有一个拥挤度。小明的妈妈虽然很着急，但是不愿意拥挤的人潮冲乱了她优雅的步伐。所以请你帮她规划一条从s至t的路线，使得经过道路的拥挤度最大值最小。

输入输出格式

输入格式：
第一行四个数字n，m，s，t。

接下来m行，每行三个数字，分别表示两个区和拥挤度。

（有可能两个区之间有多条大道相连。)

输出格式：
输出题目要求的拥挤度。

输入输出样例

输入样例#1：
3 3 1 3
1 2 2
2 3 1
1 3 3
输出样例#1：
2
说明

数据范围

30% n<=10

60% n<=100

100% n<=10000,m<=2n，拥挤度<=10000

题目保证1<=s,t<=n且s<>t，保证可以从s区出发到t区。

样例解释：

小明的妈妈要从1号点去3号点，最优路线为1->2->3。

代码：

#include
#include
#include
#include
#include
#include
#include
using namespace std;
int n,m,sl,tl;
struct nod
{
    int r,di;
}t;
vector<nod>qq[10010];
queue<int>s;
int dis[10010],vi[10010];
void SPFA(int x)
{
    int i,t;
    s.push(x);
    vi[x]=1;
    while(!s.empty())
    {
        t=s.front();
        s.pop();//出队，以后还可能再进队
        vi[t]=0;
        for(i=0;i<qq[t].size();i++)
        {
            if(dis[qq[t][i].r]>max(dis[t],qq[t][i].di))
            {
                dis[qq[t][i].r]=max(dis[t],qq[t][i].di);//松弛处理
                if(!vi[qq[t][i].r])//如果未进队，则入队
                {
                    s.push(qq[t][i].r);
                    vi[qq[t][i].r]=1;
                }
            }
        }
    }
}
int main()
{
    int i,a,b,c;
    scanf("%d%d%d%d",&n,&m,&sl,&tl);
    for(i=1;i<=m;i++)
    {
        scanf("%d%d%d",&a,&b,&c);
        t.r=b;
        t.di=c;
        qq[a].push_back(t);
        t.r=a;
        qq[b].push_back(t);
    }
    memset(vi,0,sizeof(vi));
    for(i=1;i<=n;i++) dis[i]=1e9;
    dis[sl]=0;
    SPFA(sl);
    printf("%d\n",dis[tl]);
    return 0;
}

附：
一篇讲优化的文章
文章地址