【manacher】【回文树】回文算法小结
1.manacher
manacher是一个求出以每一个字符为回文中心的回文半径的算法。其中,我们用r[i]表示以第i位为回文中心的回文半径。
鉴于回文串如果为偶数长度就不存在回文中心,我们就在每两个字符之间插入一个在原字符串里不会出现的字符:
eg.abccba——>#a#b#c#c#b#a#
显而易见的是,插入的字符不会影响原字符串的回文性质。那么我们就考虑如何处理r数组。考虑我们已经处理了i-1位,正在处理第i位。我们定义mx为当前处理过的回文串里末尾最靠后(即i+r[i]最大)的位置,p为mx对应的回文串的回文中心。那么我们会出现下面的两种情况。
case1: mx case2: mx>i 此时我们就要好好利用p的回文串的性质了。
我们就要利用i关于p的对称点j的性质了。此时我们已经知道了j的r,如果以j为中心的回文串被以p为中心的回文串包含,那么i的r就是j的r,因为i和j是对称的。如果以j为中心的回文串没有被包含,即j左端点在p的左端点的左边,那么我们依然可以利用i,j对称部分的性质,即i的r至少是mx-i,接着往后暴力更新。
由于我们暴力更新的时候都会影响mx,且mx单调不减,故算法的时间复杂度为O(N)。(代码中将case1,case2合并起来一起考虑)
代码:
char s[N],t[N];//s为原串,t为插入后的串
inline void insert()
{
int len=strlen(s),k=0;
t[0]='@';//在开头和末尾插入不同的字符防止访问越界
for(int re i=0;i<len;i++)
{
t[++k]='#';
t[++k]=s[i];
}
t[++k]='#';
t[++k]='~';
t[++k]='\0';
}
inline void work()
{
int p=0,mx=0;
int len=strlen(t);
for(int re i=0;i<len;i++)
{
r[i]=(mx>i)?(min(r[2*p-i],mx-i)):1;
while(t[i-r[i]]==t[i+r[i]])++r[i];
if(mx<r[i]+i)mx=i+r[i],p=i;
}
}
mannacher基础例题主要包括计数问题和求解最优字符串问题。
例题及更深入的应用可参考:2014年信息学奥林匹克中国国家队候选队员徐毅论文。
2.回文树
回文树是一个近年出现的新算法。
回文树是相对于一个字符串s的森林。它由两颗树构成,一颗是长度为奇数的回文子串构成的树(我们把它的root叫做odd),另一颗为长度为偶数的回文子串构成的树(我们把它的root叫做even)。其中每一个节点代表了本质不同的回文子串。u—a—>v边的含义:表示v代表的回文子串是在u的基础上分别两端增加了一个a,就是说父亲是儿子的子串。当然odd—a—>son是例外,odd直接到达的儿子就是a。如babbab对应的树(黑色边是树边):
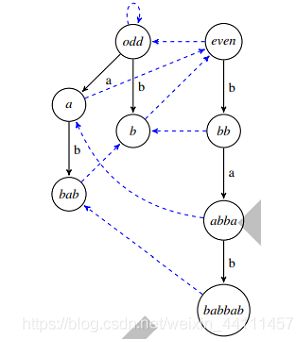
对于一个字符串的回文树的构造我们采用增量法构造。即假设我们已经构造出串s的回文树,现在我们要在s后面增加一个字符c,即构造sc的回文树。
1.首先,我们增加一个字符c,只会增加一个本质不同的字符串。这里就不赘述证明过程了,可以用反证法简单证明一下。
2.fail指针:上图中的蓝色虚线是fail指针,指向当前串的最长回文后缀,规定odd的fail是自己,even的fail是odd。
3.所以我们需要找到增加c后需要增加的节点。假设我们要增加的节点是ctc,显然t是一个回文串。所以我们就从当前字符串s的最长后缀回文串t‘开始,每次跳跃到t’的最长回文后缀上(即fail[t’]),同时每次判断t‘是否是合法的t。如果合法,则新建节点,那么我们现在只需要维护当前节点的fail即可。显而易见的,我们只需要继续跳t的fail找到第二个合法的t即是ctc的fail了。同时更新当前字符串的最长回文后缀。
4.根据势能分析,我们可以认为构造一个串s的回文树的时间复杂度是O(|s|)的。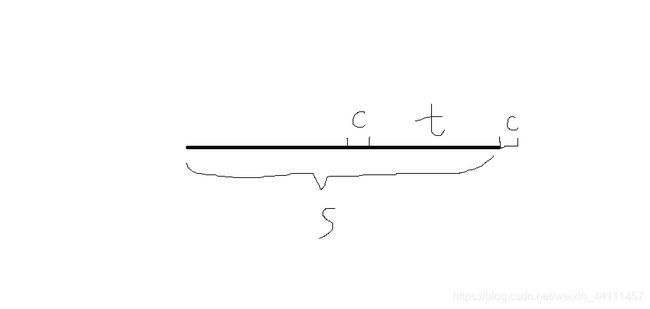
代码:
#include另外,如果存在删除操作,我们发现势能分析就可能失效。此时我们就需要一个不依靠于势能分析的插入算法。大概思路和ac自动机差不多,维护一个quick[u][c]数组直接找到插入c的合法t。这里给出代码,就不赘述更新过程了:
#include参考文献及例题:2017年国家候选队员翁文涛论文