链接
loj
luogu太水不要去了。
思路
二分。
每个军队在一定的时间内越往上越好。
注意一个军队可以跨过1去帮别的。
把能到1脚下的点都存下来特判。
有一种情况是这个子树内只有一个军队,但这个军队跑去帮别人了。
其他军队来帮这个子树。
就像这样。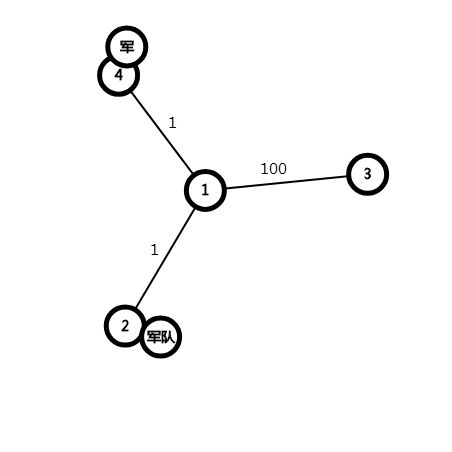
四号点的军队还有2秒钟,而且四号点有两个军队。
2号点有一个军队,还有101秒钟。
三号点没有军队。
四号点的一个军队到2,二号点的的军队到三。
这样的2号点放弃内部去外部的条件是什么?
答案是两倍的边权<剩余时间。
不然的话,四号店可以直接去拯救三号点了。
代码R的范围小了点,卡场过loj
代码
#include
#include
#include
#include
#include
#define ll long long
using namespace std;
const int _=3e5+7;
const ll oo=0x3f3f3f3f3f3f3f;
char buf[10000001],*p1=buf,*p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,10000000,stdin),p1==p2)?EOF:*p1++)
int read() {
int x=0,f=1;char s=getchar();
for(;s>'9'||s<'0';s=getchar()) if(s=='-') f=-1;
for(;s>='0'&&s<='9';s=getchar()) x=x*10+s-'0';
return x*f;
}
int n,m,pos[_],fa[_][19],vis[_],head[_],tot,ok[_];
ll sum[_],nb[_],cb[_];
struct node {int v,nxt,q;}e[_<<1];
void add(int u,int v,int q) {e[++tot].v=v,e[tot].q=q,e[tot].nxt=head[u],head[u]=tot;}
void init(int u,int f,ll tot) {
fa[u][0]=f,sum[u]=tot;
for(int i=head[u];i;i=e[i].nxt)
if(e[i].v!=f) init(e[i].v,u,tot+e[i].q);
}
bool dfs(int u,int fa) {
if(vis[u]) return 1;
int siz=0;
for(int i=head[u];i;i=e[i].nxt) {
int v=e[i].v;
if(v==fa) continue;
siz++;
if(!dfs(v,u)) return 0;
} return siz;
}
vector dsr[_];
bool cmp(int a,int b) {return sum[a]=0;--j)
if(sum[pos[i]]-sum[fa[p][j]]<=mid)
p=fa[p][j];
if(fa[p][0]!=1) vis[p]++;
else dsr[p].push_back(pos[i]);
}
for(int i=head[1];i;i=e[i].nxt) ok[e[i].v]=dfs(e[i].v,1);
for(int i=head[1];i;i=e[i].nxt) sort(dsr[e[i].v].begin(),dsr[e[i].v].end(),cmp);
for(int i=head[1];i;i=e[i].nxt) {
int v=e[i].v;
if(!ok[v] && dsr[v].size()) {
ll x=mid-sum[dsr[v][dsr[v].size()-1]];
if(e[i].q*2LL>=x) dsr[v].pop_back(),ok[v]=1;
}
}
int cnt=0,gs=0;
for(int i=head[1];i;i=e[i].nxt) {
int v=e[i].v;
for(int j=0;j<(int)dsr[v].size();++j)
nb[++cnt]=mid-sum[dsr[v][j]];
if(!ok[v]) cb[++gs]=e[i].q;
}
sort(nb+1,nb+1+cnt,greater());
sort(cb+1,cb+1+gs,greater());
if(cntnb[i]) return 0;
return 1;
}
int main() {
n=read();
for(int i=1;i=0;--i)
if(check(ans-(1LL<