PR17.10.4:Q-Prop: Sample-Efficient Policy Gradient with An Off-Policy Critic
What’s problem?
- A major obstacle facing deep RL in the real world is their high sample complexity. Batch policy gradient methods offer stable learning, but at the cost of high variance, which often requires large batches.
- TD-style methods, such as off-policy actor-critic and Q-learning, are more sample-efficient but biased, and often require costly hyperparameter sweeps to stabilize.
- The on-policy method provides an almost unbiased, but high variance gradient, while the off-policy method provides a deterministic, but biased gradient.
What’s the challenges?
(1) The standard form of Monte carlo policy gradient methods is shown below:
- The gradient is estimated using Monte Carlo samples in practice and has very high variance. A proper choice of baseline b(st) is necessary to reduce the variance sufficiently such that learning becomes feasible.
- Another problem with the policy gradient is that it requires on-policy samples. This makes policy gradient optimization very sample intensive.
(2) Policy gradient methods with function approximation or actor-critic methods, include a policy evaluation step, which often uses temporal difference (TD) learning to fit a critic Qw for the current policy π(θ) , and a policy improvement step which greedily optimizes the policy π against the critic estimate Qw .
The gradient in the policy improvement phase is given below:
These properties make DDPG and other analogous off-policy methods significantly more sample-efficient than policy gradient methods. Howerver, the biased policy gradient estimator makes analyzing its convergence and stability properties difficult.
What’s the STOA?
In this paper, they propose Q-Prop, a step in this direction that combines the advantages of on-policy policy gradient methods with the efficiency of off-policy learning. Q-Prop can reduce the variance of gradient estimator without adding bias.
What’s the proposed solution?
(1) To derive the Q-Prop gradient estimator, we start by using the first-order Taylor expansion of an arbitrary function f(st,at) .
A sensible choice is to use the critic Qw for f and μθ(st) for at to get:
In practice, we estimate advantages A^(st,a) , we write the Q-Prop estimator in terms of advantages to complete the basic derivation.

(2) Control variate analysis and adaptive Q-prop
A weighing variable that modulates the strength of control variate. This additional variable η(st) does not introduce bias to the estimator.
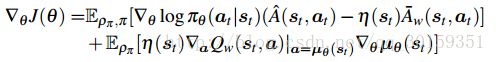

注:(10)的推导没有看明白,但从公式(11)可以看到variance的大小可以由协方差前的 −2η(st) 控制。
Additionally, the paper introduce two additional variants of Q-Prop. (Adaptive Q-Prop, Conservative and Aggressive Q-Prop. See paper for details)
Pseudo-code:

source code:
https://github.com/shaneshixiang/rllabplusplus
What’s the performance of the proposed solution?

Figure 2b shows the performance of conservative Q-Prop against TRPO across different batch sizes. Due to high variance in gradient estimates, TRPO typically requires very large batch sizes.

Figure 3a shows that c-Q-Prop methods significantly outperform the best TRPO and VPG methods. DDPG on the other hand exhibits inconsistent performances. With proper reward scaling, i.e. “DDPG-r0.1”, it outperforms other methods as well as the DDPG results reported in prior work (Duan et al., 2016; Amos et al., 2016). This illustrates the sensitivity of DDPG to hyperparameter settings, while Q-Prop exhibits more stable, monotonic learning behaviors when compared to DDPG.

They evaluate Q-Prop against TRPO and DDPG across multiple domains.
Conclusion
They presented Q-Prop, a policy gradient algorithm that combines reliable, consistent, and potentially unbiased on-policy gradient estimation with a sample-efficient off-policy critic that acts as a control variate. The method provides a large improvement in sample efficiency compared to stateof-the-art policy gradient methods such as TRPO, while outperforming state-of-the-art actor-critic methods on more challenging tasks such as humanoid locomotion.