leetcode经典堆相关题目(思路、方法、code)

用于回顾数据结构与算法时刷题的一些经验记录
堆的题目大多还是较为复杂的

215. 数组中的第K个最大元素

在未排序的数组中找到第 k 个最大的元素。请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

示例 1:
输入: [3,2,1,5,6,4] 和 k = 2
输出: 5

分析：Topk问题，属于堆的非常基础的应用了。

如果采用排序的方式，然后返回对应位置元素，则时间复杂度为 $O(nlogn)$

采用堆的方法：

• 维护一个K大小的最小堆
• 将数组中元素按顺序push进入堆
• push时，如果堆中元素小于K个，则新元素直接进入堆；否则，如果堆顶小于新元素，则弹出堆顶，将新元素加入堆

通过该操作，我们可知，最终堆中的K个元素，是最大的K个元素(因为任何比较小的元素，都会被弹出堆顶)，且堆的顶部就是要求的第K大的数。

算法复杂度为 $O(nlogk)$

class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) 
	{
		priority_queue<int,vector<int>,greater<int> > Q;//创建一个最小堆
		for(int i=0;i<k;i++)
			Q.push(nums[i]);
		for(int i=k;i<nums.size();i++)
		{
			if(Q.top()<nums[i]) //Q的顶部小于当前元素,将堆顶pop,将新元素push
			{
				Q.pop(); 
				Q.push(nums[i]);
			}
		}
		return Q.top();
    }
};

347. 前 K 个高频元素

给定一个非空的整数数组，返回其中出现频率前 k 高的元素。

示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]

分析：首先利用MAP的方式对元素进行计频，即形成 (元素->次数) 的映射关系，将该映射关系存放到一个结构体中，方便利用该结构体对堆进行排序。然后通过最小堆找到前k个高频元素 。我在这个题用到了 结构体、重构operator，map ，堆等多种方式，也算是一个很好的温习。

struct Node{  //用来存数字->频率的映射
	int x,y;
	Node(int a=0, int b=0):
		x(a), y(b) {}
};

struct cmp{
	bool operator()(Node a, Node b)
	{
		return a.y>b.y;
	}
};

class Solution {
public:
    vector<int> topKFrequent(vector<int>& nums, int k) 
	{
		priority_queue<Node,vector<Node>,cmp> Q;//创建一个最小堆
		map<int,int> MAP;
		vector<int> result;
		for(int i=0;i<nums.size();i++)
			MAP[nums[i]]++;
		map<int, int>::iterator iter;
		int kk=0;
		for(iter = MAP.begin();iter!=MAP.end();iter++)
		{
			if(kk<k)
			{
				Q.push(Node(iter->first,iter->second));
				kk++;
			}
			else if(Q.top().y<iter->second)
			{
				Q.pop();
				Q.push(Node(iter->first,iter->second));
			}
		}
		while(!Q.empty())
		{
			result.push_back(Q.top().x);
			Q.pop();
		}
		return result; 
    }
};

295. 数据流的中位数

中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。

例如， [2,3,4] 的中位数是 3 ； [2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：

void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。

示例：
addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3) 
findMedian() -> 2

分析： 动态维护数据的中位数(意味着添加数据后中位数也将动态改变)

比较直观的方法：

用数组存数据，每次添加元素或者查询中位数时对数组排序，然后计算结果

• 如果添加元素时排序(插入排序)，则添加元素复杂度为 $O(n)$ 找中位数复杂度为 $O(1)$
• 如果查询中位数时候排序(查询时可以快排之类的)，则插入元素复杂度 $O(1)$ 找中位数复杂度为 $O(nlogn)$

一个很棒的方法是：巧妙利用堆的性质，实现该功能

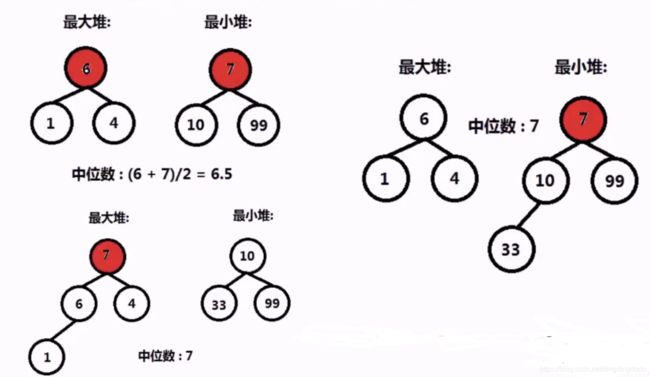
动态维护一个最大堆和最小堆，每个堆存储一半数据，且维持最大堆的堆顶比最小堆的堆顶小

如图所示，当两个堆数量相同时，中位数就是两个堆顶的平均，否则就是数量多1的那个堆的堆顶。

因此，如何维持这两个堆呢？

分为三种情况，两堆元素数量相同，最大堆元素数量小于最小堆元素数量，最大堆元素数量大于最小堆元素数量。

当两个堆数量相同时，如果新加入的元素小于最大堆的堆顶，则将其放入最大堆，如果其大于最大堆的堆顶，则将其放入最小堆

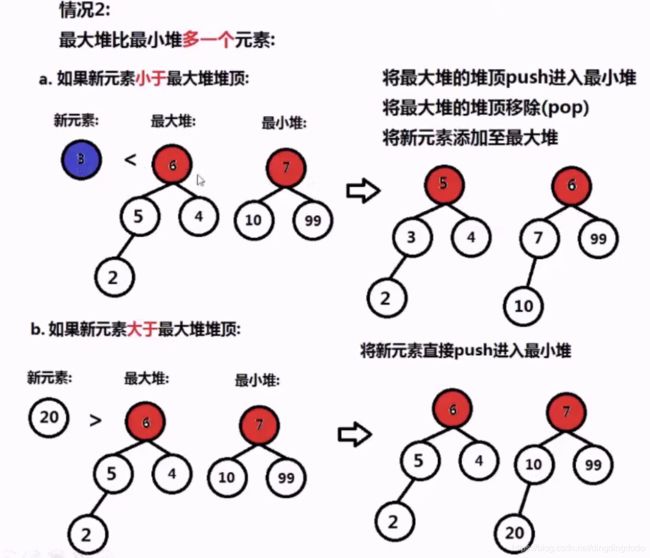
如果最大堆比最小堆多一个元素：

• 如果新元素小于最大堆的堆顶，则将最大堆的堆顶移到到最小堆，将新元素加入到最大堆
• 如果新元素大于最大堆的堆顶，则将其加入到最小堆即可

如果最大堆比最小堆少一个元素：

• 如果新元素小于最小堆的堆顶，则将其加入最大堆
• 如果新元素大于最小堆的堆顶，将最小堆堆顶移到最大堆，将新元素加入最小堆即可

class MedianFinder {
public:
    /** initialize your data structure here. */
    priority_queue<int,vector<int>,greater<int> > small;
        priority_queue<int,vector<int>,less<int> > big;
    MedianFinder() 
	{

    }
    
    void addNum(int num) 
	{
		if(big.empty())  //最大堆为空，将其加入
		{
			big.push(num);
			return;
		}
		if(big.size()==small.size()) //两个堆元素数量相同
		{
			if(num<big.top())
				big.push(num);
			else
				small.push(num);
		}
		else if(big.size()>small.size()) //最大堆元素数量大于最小堆元素数量
		{
			if(num>big.top())
				small.push(num);
			else{
				small.push(big.top());
				big.pop();
				big.push(num);	
			 }
		}
		else  //最大堆元素数量小于最小堆元素数量
		{
			if(num<small.top())
				big.push(num);
			else{
				big.push(small.top());
				small.pop();
				small.push(num);
			}
				
		}
    }
    
    double findMedian()  //根据两个堆的元素数量判断
	{
	 	if(small.size()==big.size())
	 	return (double(small.top())+big.top())/2;
	 	else if(small.size()<big.size())
	 	return big.top();
		else
		return small.top();
    }
};

871. 最低加油次数

汽车从起点出发驶向目的地，该目的地位于出发位置东面 target 英里处。

沿途有加油站，每个 $station[i]$ 代表一个加油站，它位于出发位置东面 $station[i][0]$ 英里处，并且有 $station[i][1]$ 升汽油。

假设汽车油箱的容量是无限的，其中最初有 $startFuel$ 升燃料。它每行驶 1 英里就会用掉 1 升汽油。

当汽车到达加油站时，它可能停下来加油，将所有汽油从加油站转移到汽车中。

为了到达目的地，汽车所必要的最低加油次数是多少？如果无法到达目的地，则返回 -1 。

注意：如果汽车到达加油站时剩余燃料为 0，它仍然可以在那里加油。如果汽车到达目的地时剩余燃料为 0，仍然认为它已经到达目的地。

示例 1：

输入：target = 1, startFuel = 1, stations = []
输出：0
解释：我们可以在不加油的情况下到达目的地。

分析：

将问题换个角度想，汽车每经过一个加油站 $i$ ,实际上便等价于获得了一次在任何时候都能加 $station[i][1]$单位汽油的权利。则在之后需要加油的时候，可以加上之前经过的加油站可加的油。 因此利用贪心的思想，**每次等到汽油没时候，加可加的最大的油量。因此便可以将路过的加油站可加的油量加入到优先队列
当油量空时候：如果优先队列为空，则无法到达终点 否则，取出优先队列的最大元素加入油箱

尽可能不加油，每路过一个地方即将该地点的加油量加入到最大堆，如果汽车没油了且还没有到达终点，则在此时加最大堆堆顶的油(等价于路过该加油站时候加了油)，继续前进，直至不能到达或者达到。
首先遍历每个加油站，将能路过的加油站的油量加入到heap中。遍历完加油站还没有到达终点的话则直接一直加最大的油量并判断即可。

class Solution {
public:
    int minRefuelStops(int target, int startFuel, vector<vector<int> >& stations) 
	{
		int pos=0; //当前位置 
		int fuel=startFuel; //油量
		int times=0; //加油次数
		priority_queue<int,vector<int>,less<int> > big_heap; //最大堆
		int nums=stations.size();//加油站数量
		for(int i=0;i<nums;i++) //先遍历加油站，能路过则将其加入heap中
		{
			if(pos>=target) return times;
			int d=stations[i][0]-pos;//到下一个加油站的距离
			while(fuel-d<0)    //当前到不了下一个加油站 
			{
			if(big_heap.empty())   //没油了			
				return -1;
			fuel+=big_heap.top(); //将最大的油量加入
			big_heap.pop();  //pop出最大值
			times++;     //加油次数加1 
		   	} //退出循环意味着走过了这个加油站 
		   	big_heap.push(stations[i][1]);
		   	pos=stations[i][0];
		   	fuel-=d;	   
		}
		//走完加油站了 
		pos+=fuel;
		if(pos>=target) 
		 	return times;
    	while(!big_heap.empty()) //耗完油还没到，那就直接一直pop一直判断
		{
			pos+=big_heap.top();
			big_heap.pop(); 
			times++;
			if(pos>=target) 
		 		return times;
		}
		return -1;
    }
};