43. Multiply Strings(字符串相乘)解法(C++ & 注释)
43. Multiply Strings(字符串相乘)
- 1. 题目描述
- 2. 乘法(Multiplication)
- 2.1 解题思路
- 2.2 实例代码
1. 题目描述
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
示例 1:
输入: num1 = “2”, num2 = “3”
输出: “6”
示例 2:
输入: num1 = “123”, num2 = “456”
输出: “56088”
说明:
- num1 和 num2 的长度小于110。
- num1 和 num2 只包含数字 0-9。
- num1 和 num2 均不以零开头,除非是数字0 本身。
- 不能使用任何标准库的大数类型(比如 BigInteger)或直接将输入转换为整数来处理。
题目链接:中文题目;英文题目
2. 乘法(Multiplication)
2.1 解题思路
这题和415. 字符串相加非常像,之前的题目可以先反转两个字符串,然后从序号0到序号max(字符串大小1,字符串大小2) - 1,如果访问的字符串序号越界,则相当于加0,然后同序号的两数相加。最后从左往右检查进位,如果多出来数字则在新数组末尾添加一个,之后从右往左跳过0,将数字转化成字符,组合成最终答案即可。
这题的思路有一部分和415. 字符串相加是一样的,因为乘法是先错位相乘,然后每位数相加,然后检查进位。后面相加部分都是字符串加法是一致。所以这里我们着重讨论一下错位相乘。我们以下面这个例子为例:
[“123”, “45”], ans = “5535”
首先我们先来看看数字乘法和字符串乘法的流程图:
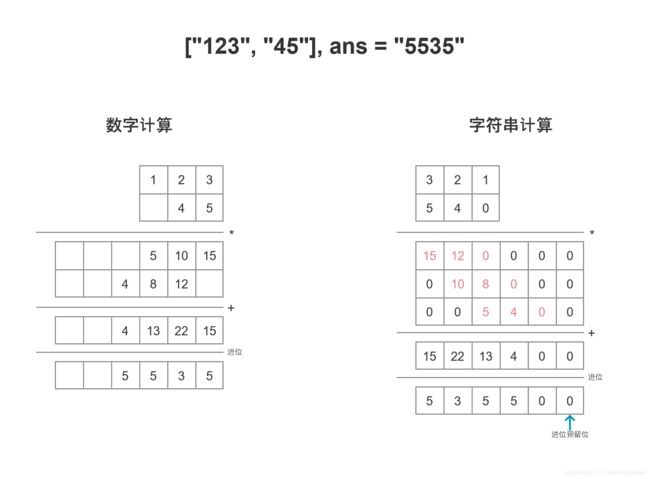
左边就是我们都会的乘法计算,而右边是字符串乘法。对于字符串乘法,有一个问题需要先解决:如果两数的位数不相等。这种情况,我们用0补齐长度小的字符串,然后进行翻转,因为我们要对齐两个字符串,这样就可以使用序号判断来补齐0,而不用实际往字符串中添加0。之后就是错位乘法了,我们观察上面的例子发现,字符串长度为3时,第一次相乘(3 * 54),对应需要叠加的数字序号为:0,1,2,然后回到1,开始下一次相乘(2 * 54) :1,2,3,然后再回到2,继续下一次相乘(1 * 54):2,3,4,所以每次相乘后,序号需要回溯len - 1个位置。
我这里初始化叠加数组的时候,预留了一个进位预留位,保证相加的时候不会序号越界。那么叠加数组的长度怎么来的呢?因为两个长度为len的数相乘,会错位n - 1个位置,所以最后的长度为:n + ( n - 1),然后 + 1个进位预留位。那么这样最后进位的时候会不会越界呢?我们考察一下最大的两数相乘,假设字符串最大长度为3:999 * 999 = 998001,就是说3位数相乘,不会超过6位数,所以我们初始化2 * maxLen个位置的叠加数组,是一定不会越界的。
最后需要提醒一下:和字符串加法不同,乘法进位会大于1,而加法不会;
2.2 实例代码
class Solution {
public:
string multiply(string num1, string num2) {
int len1 = num1.size(), len2 = num2.size(), maxLen = max(len1, len2), idx = 0, moves = maxLen - 1,
lenAns = 2 * maxLen; // lenAns = maxLen + (maxLen - 1) + 1
if (!len1 || !len2) return ""; // corner cases: [", ""], ["1", ""], ["", "1"]
vector<int> nums(lenAns, 0);
reverse(num1.begin(), num1.end());
reverse(num2.begin(), num2.end());
for (int i = 0; i < maxLen; i++) {
for (int j = 0; j < maxLen; j++) {
int temp = (i >= len1 ? 0 : num1[i] - '0') * (j >= len2 ? 0 : num2[j] - '0');
nums[idx++] += temp;
}
idx -= moves;
}
// 进位检查
for (int i = 0; i < lenAns - 1; i++)
if (nums[i] > 9) { int temp = nums[i]; nums[i] = temp % 10; nums[i + 1] += temp / 10; }
string ans;
idx = lenAns - 1;
while (idx >= 0 && !nums[idx]) idx--; // 去掉前面多余的0
if (idx == -1) idx++; // corner case: ["0", "0"]
for (; idx >= 0; idx--) ans.push_back(nums[idx] + '0');
return ans;
}
};