94. Binary Tree Inorder Traversal（二叉树的中序遍历）两种解法（C++ & 注释）

1. 题目描述

给定一个二叉树，返回它的中序 遍历。

示例:

进阶: 递归算法很简单，你可以通过迭代算法完成吗？

题目链接：中文题目；英文题目

2. 递归（Recursion）

2.1 解题思路

我推荐大家把二叉树的三种遍历方式一起看了，对比理解，加深记忆（链接更新中，可先到个人主页查看）：

1. 二叉树三种遍历实现串讲（前中后序遍历） - 推荐；
2. Binary Tree Preorder Traversal（二叉树的前序遍历）；
3. Binary Tree Postorder Traversal（二叉树的后序遍历）；

递归方法非常的简单，首先我们先来看看中序遍历的顺序：

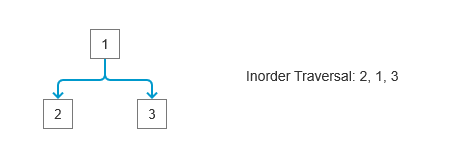
可以看到，中序遍历先找到左节点，然后打印当前节点，再找到右节点，所以整个递归访问顺序为：

inorderRecursion(root->left); // 往左走
ans.push_back(root->val); // 加入数组
inorderRecursion(root->right); // 往右走

2.2 实例代码

class Solution {
    vector<int> ans;

    void inorderRecursion(TreeNode* root) {
        if (!root) return;

        inorderRecursion(root->left);
        ans.push_back(root->val);
        inorderRecursion(root->right);
    }

public:
    vector<int> inorderTraversal(TreeNode* root) {
        inorderRecursion(root);
        return ans;
    }
};

3. 迭代（Iteration）

3.1 解题思路

迭代的方法稍微要难一些，我们还是使用列队（Queue）来实现，主要思路和之前说的前序遍历是基本一样的，只是和前序遍历不同，我们要先加入左节点，然后把当前节点放在左节点之后，最后才是右节点。

但是这样做也会遇到一个问题：1之前已经处理过了，之后再遇到1会造成无限循环，所以需要对之前处理过的节点进行修改。我们先简化一下二叉树，深度限制为2，即节点仅有1、2、3；按照上述方法处理，queue的元素为：2、1、3，我们发现2和3不会出现重复处理的问题，因为它们为叶节点，而1因为不为叶节点，所以可以考虑添加左右节点之后，把该节点的左右指针指向空，避免之后重复处理的问题；其他思路和前序遍历保持一致，思路流程图如下图所示：

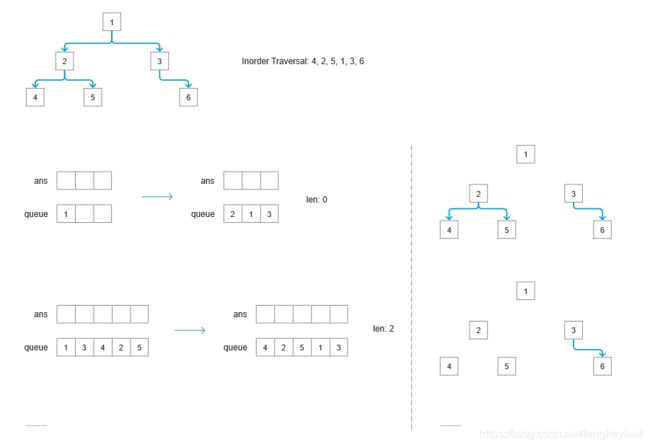
另外，也可以使用stack来实现，思路差异不大，大家可以自己尝试做做，或者参考这篇文章的代码：Golang iterative solution using a stack with docs. 100% runtime.

3.2 实例代码

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
   	 	vector<int> ans;
        if (!root) return ans;
        
        queue<TreeNode*> q;
        q.push(root);

        while (q.size()) {
            TreeNode* temp = q.front();
            q.pop();
            int len = q.size();

            if (!temp->left && !temp->right) { ans.push_back(temp->val); continue; }

			// 中序遍历节点顺序重组
            if (temp->left) { q.push(temp->left); temp->left = nullptr; }
            q.push(temp);
            if (temp->right) { q.push(temp->right); temp->right = nullptr; }

            for (int i = 0; i < len; i++) { q.push(q.front()); q.pop(); }
        }
        
        return ans;
    }
};