二叉树三种遍历实现串讲（前中后序遍历 & C++）

1. 递归（Recursion）

1.1 解题思路

这篇文章把二叉树三种遍历的实现方法连贯起来讲解一下，这样利于大家进行对比，更利于理解；三种遍历方法的单独讲解文章链接：

1. Binary Tree Preorder Traversal（二叉树的前序遍历）；
2. Binary Tree Inorder Traversal（二叉树的中序遍历）；
3. Binary Tree Postorder Traversal（二叉树的后序遍历）；

我们从前序遍历开始，先看看前序遍历的访问顺序：

可以看到，前序遍历走到哪个节点，就先把打印出该节点的值；所以加入数组的操作为第一步（ans.push_back(root->val)）。那么剩下的问题就是先往左还是先往右了，从上面的例子很明显是先往左再往右，所以整个递归访问顺序为：

ans.push_back(root->val); // 先加入数组
preorderRecursion(root->left); // 向左走
preorderRecursion(root->right); // 向右走

接着是中序遍历：

可以看到，中序遍历先找到左节点，然后打印当前节点，再找到右节点，所以整个递归访问顺序为：

inorderRecursion(root->left); // 往左走
ans.push_back(root->val); // 加入数组
inorderRecursion(root->right); // 往右走

最后是后序遍历：

后序遍历和中序遍历比较相似，不同的是后序遍历走完左边，再走右边，最后才打印当前节点，所以整个递归访问顺序为：

postorderRecursion(root->left); // 往左走
postorderRecursion(root->right); // 往右走
ans.push_back(root->val); // 添加当前节点

三种遍历顺序的递归方法，都是先左后右，只是添加当前节点的顺序不一样：

1. 前序：先于寻找左右节点添加；
2. 中序：在左节点之后添加，但先于右节点；
3. 后序：在寻找左右节点之后添加；

1.2 实例代码

class Solution {
    vector<int> ans;

	// 1. 前序遍历
    void preorderRecursion(TreeNode* root) {
        ans.push_back(root->val);
        preorderRecursion(root->left);
        preorderRecursion(root->right);
    }

	// 2. 中序遍历
    void inorderRecursion(TreeNode* root) {
        inorderRecursion(root->left);
        ans.push_back(root->val);
        inorderRecursion(root->right);
    }
    
    // 3. 后序遍历
        void postorderRecursion(TreeNode* root) {
        postorderRecursion(root->left);
        postorderRecursion(root->right);
        ans.push_back(root->val);
    }
    
public:
    vector<int> preorderTraversal(TreeNode* root) {
        if (!root) return;
        
        // 三种遍历顺序的递归方法 - 前序、中序、后序
        // preorderRecursion(root);
        // inorderRecursion(root);
        postorderRecursion(root);
        
        return ans;
    }
};

2. 迭代（Iteration）

2.1 解题思路

2.1.1 前序遍历

三种遍历方法都可以用Queue和Stack来实现，其中前序遍历用列队（Queue）更好，后序遍历用栈（Stack）更好，因为前序遍历的特点为：“先到先得”，这个特点让我们想到了某个数据结构的特点：“先进先出”，也就是列队（Queue）的特点；后序遍历遵循“先进后得”的特点（先右后左添加节点），和stack“先进后出”的特点相匹配，

我们用一个比递归稍微复杂一点的例子来说明迭代的思路。首先是前序遍历：

首先，把1加入queue中，根据“先到先得”原则，取出1，加入ans数组中，然后把1左右两个节点加入queue中；接下来和之前一样，取出2，加入ans中，把4和5加入queue中，到这里我们遇到了一个问题：3在4和5的前面，但是遍历顺序应该先4和5，再3：

所以我们需要把未加入新节点之前的所有节点全部放在新节点的后面，所以在弹出2之后，需要先记录queue现在的长度，再加入4和5之后，将前面的节点放在他们后面：

之后的步骤和上面的完全一样，重复执行直到queue里面没有任何元素，即完成了前序遍历。这部分对应代码：2.2.1 前序遍历。另外，也可以使用stack来实现，思路差异不大，大家可以自己尝试做做，或者参考这篇文章的代码：C++ solution || recursive || iterative || stack based

2.1.2 中序遍历

中序遍历和前序遍历使用Queue是基本一样的，只是和前序遍历不同，我们要先加入左节点，然后把当前节点放在左节点之后，最后才是右节点。

但是这样做也会遇到一个问题：当前节点之前已经处理过了，之后再遇到它会造成无限循环，所以需要对之前处理过的节点进行修改。我们先简化一下二叉树，深度限制为2，即节点仅有1、2、3；按照上述方法处理，queue的元素为：2、1、3，我们发现2和3不会出现重复处理的问题，因为它们为叶节点，而1因为不为叶节点，所以可以考虑添加左右节点之后，把该节点的左右指针指向空，避免之后重复处理的问题；其他思路和前序遍历保持一致，思路流程图如下图所示：

这部分对应代码：2.2.2 中序遍历

另外，也可以使用stack来实现，思路差异不大，大家可以自己尝试做做，或者参考这篇文章的代码：Golang iterative solution using a stack with docs. 100% runtime.

2.1.3 后序遍历

最后是后序遍历的Queue用法，几乎和中序遍历没有区别，只是添加节点的顺序稍微有点区别（左 -> 右 -> 当前）。所以我们重点来看看使用stack的思路，对应流程图如下，大家看一下就明白了啦，不难哒：

这部分对应代码：2.2.3 后序遍历

2.2. 实例代码

2.2.1 前序遍历

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> ans;
        if (!root) return ans;

        queue<TreeNode*> q;
        q.push(root);

        while (q.size()) {
            TreeNode* temp = q.front();
            q.pop();

            int len = q.size();
            ans.push_back(temp->val);

            if (temp->left) q.push(temp->left);
            if (temp->right) q.push(temp->right);

            for (int i = 0; i < len; i++) { q.push(q.front()); q.pop(); }
        }

        return ans;
    }
};

2.2.2 中序遍历

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
   	 	vector<int> ans;
        if (!root) return ans;
        
        queue<TreeNode*> q;
        q.push(root);

        while (q.size()) {
            TreeNode* temp = q.front();
            q.pop();
            int len = q.size();

            if (!temp->left && !temp->right) { ans.push_back(temp->val); continue; }

			// 中序遍历节点顺序重组
            if (temp->left) { q.push(temp->left); temp->left = nullptr; }
            q.push(temp);
            if (temp->right) { q.push(temp->right); temp->right = nullptr; }

            for (int i = 0; i < len; i++) { q.push(q.front()); q.pop(); }
        }
        
        return ans;
    }
};

2.2.3 后序遍历

class Solution {
    vector<int> ans;
    
    // 1. 使用queue的迭代
    void iterationUsingQueue(TreeNode* root) {
        queue<TreeNode*> q;
        q.push(root);

        while (q.size()) {
            TreeNode* temp = q.front();
            q.pop();
            int len = q.size();

            if (!temp->left && !temp->right) { ans.push_back(temp->val); continue; }

            // 后序遍历顺序重组
            if (temp->left) { q.push(temp->left); temp->left = nullptr; }
            if (temp->right) { q.push(temp->right); temp->right = nullptr; }
            q.push(temp);

            for (int i = 0; i < len; i++) { q.push(q.front()); q.pop(); }
        }

    }

    // 2. 使用stack的迭代
    void iterationUsingStack(TreeNode* root) {
        stack<TreeNode*> s;
        s.push(root);

        while (s.size()) {
            TreeNode* temp = s.top();
            
            if (!temp->left && !temp->right) { ans.push_back(temp->val); s.pop(); continue; }

            if (temp->right) { s.push(temp->right); temp->right = nullptr; }
            if (temp->left) { s.push(temp->left); temp->left = nullptr; }
        }
    }

public:
    vector<int> postorderTraversal(TreeNode* root) {
        if (!root) return ans;
        //iterationUsingQueue(root); 
        iterationUsingStack(root); 

        return ans;
    }
};

3. 总结（Summary）

先来看看三种遍历顺序的流程图：

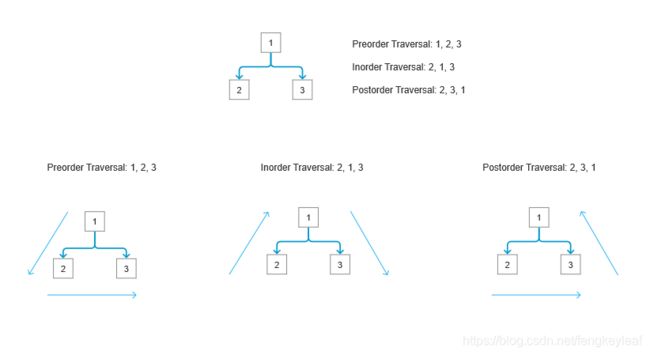
三种遍历顺序的递归方法，都是先左后右，只是添加当前节点的顺序不一样：

1. 前序：先于寻找左右节点添加；
2. 中序：在左节点之后添加，但先于右节点；
3. 后序：在寻找左右节点之后添加；

对于迭代使用Queue：

1. 前序遍历按顺序添加（当前 -> 左 -> 右），然后取出最前面的元素，放在答案数组之中，记录当前queue长度，添加当前节点的左右两个节点，最后把queue中前面的旧节点放在最后即可；

2. 中序遍历需要调整添加节点顺序：左 -> 当前 -> 右。因为当前节点处理一次后会放回queue之中，所以添加左右节点之后，需要把当前节点的左右指针指向空，避免重复处理的情况，其余思路和前序遍历保持一致；

3. 后序遍历也需要调整添加节点顺序：左 -> 右 -> 当前 ，其余思路和中序遍历保持一致；

最后前序遍历用列队（Queue）更好，后序遍历用栈（Stack）更好，因为前序遍历的特点为：“先到先得”，这个特点让我们想到了某个数据结构的特点：“先进先出”，也就是列队（Queue）的特点；后序遍历遵循“先进后得”的特点（先右后左添加节点），和stack“先进后出”的特点相匹配；前序和中序遍历理论上也可以使用stack来实现，大家可以自己探索以下~