【强化学习】Policy Gradient

原文链接：https://www.yuque.com/yahei/hey-yahei/rl-policy_gradient

参考：

• 机器学习深度学习（李宏毅）- Deep Reinforcemen Learning3_1
• 机器学习深度学习（李宏毅）- Policy Gradient
• 机器学习深度学习（李宏毅）- Proximal Policy Optimization

策略梯度

策略梯度（Policy Gradient）是一种policy-based的RL算法。

基本形式

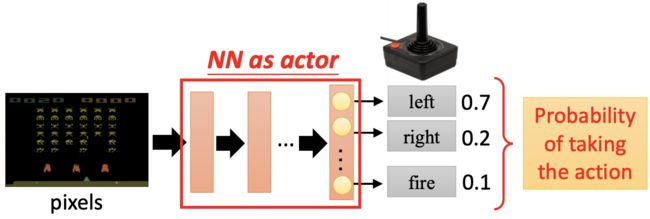
将游戏图像输入给神经网络，输出各个动作的决策概率，在预测阶段直接挑选概率最大的动作，在训练阶段则按照概率随机执行动作。
我们用采取某个动作之后的奖励总和（包括后续动作产生的奖励）来评估执行者actor的好坏，也即
$$R_{\theta }=\sum _{t=1}^T{r}_t$$
其中，$$r_t$$是采取该动作后第$$t$$个状态所获的奖励。
由于状态的复杂多变，以及每次采取动作的随机性，这里的$$R_{\theta }$$显然是一个随机变量，实际操作中我们使用它的期望$${\bar{R}}_{\theta }$$来评估执行者$${\pi }_{\theta }(s)$$的好坏。

记一个动作序列（通常成为片段episode）为
$$\tau =\{{\tau }_1,{\tau }_2,...,{\tau }_T\}$$
$${\tau }_i=(s_i,a_i,r_i)$$表示该片段中第$$i$$个状态$$s_i$$下采取动作$$a_i$$后获得了奖励$$r_i$$；

【这里强调一下上下标的含义，上标代表采样序号，下标代表本次采用的时间序号，如下文的$${\tau }_t^n$$代表第$$n$$次采样中，第$$t$$个时间点的阶段（三元组$$s_t^n,a_t^n,r_t^n$$）；另外，$$r$$和$$\tau$$长得可太像了，千万别看错！】

实际中我们几乎不可能遍历所有可能的动作序列，一般都是通过$$N$$次采样的平均结果来估计期望，也即
$${\bar{R}}_{\theta }=\sum _{\tau }R(\tau )P(\tau |\theta )\approx \frac{1}{N}\sum _{n=1}^{N}R\left({\tau }^n\right)$$
我们的目标是最大化奖励期望，即
$${\theta }^{\ast }=\arg \underset{\theta }{\max }{\bar{R}}_{\theta }$$
自然而然想到，可以用梯度上升法迭代更新权重
$${\theta }^{t+1}\leftarrow {\theta }^t+\eta \nabla {\bar{R}}_{{\theta }^t}$$
接下来考虑如何求解$$\nabla {\bar{R}}_{\theta }$$，直接对$$\overline{R_{\theta }}$$求导
$$\nabla {\bar{R}}_{\theta }=\sum _{\tau }R(\tau )\nabla P(\tau |\theta )$$
注意$$R(\tau )$$跟$$\theta$$无关，它不需要可导，即使是个黑盒都无关紧要；而
$$P(\tau |\theta )=p\left(s_1\right)\prod _{t=1}^{T}p\left(a_t|s_t,\theta \right)p\left(r_t,s_{t+1}|s_t,a_t\right)$$
这里$$p\left(s_1\right)$$和$$p\left(r_t,s_{t+1}|s_t,a_t\right)$$都与$$\theta$$无关，看起来可太碍事了，不如我们取个对数
$$logP(\tau |\theta )=\log p\left(s_1\right)+\sum _{t=1}^T\log p\left(a_t|s_t,\theta \right)+\log p\left(r_t,s_{t+1}|s_t,a_t\right)$$
显然，
$$\nabla \log P(\tau |\theta )=\sum _{t=1}^T\nabla \log p\left(a_t|s_t,\theta \right)$$
这可干净多了。为了应用对数形式的梯度，那么将奖励梯度做一下简单变换，
$$\begin{array}{rlrl}\nabla {\bar{R}}_{\theta }& =\sum _{\tau }R(\tau )\nabla P(\tau |\theta )& & \\ & =\sum _{\tau }R(\tau )P(\tau |\theta )\frac{\nabla P(\tau |\theta )}{P(\tau |\theta )}& & \\ & =\sum _{\tau }R(\tau )P(\tau |\theta )\nabla \log P(\tau |\theta )& & 【\frac{\mathrm{dlog}(f(x))}{dx}=\frac{1}{f(x)}\frac{df(x)}{dx}】\\ & \approx \frac{1}{N}\sum _{n=1}^{N}R\left({\tau }^n\right)\nabla \log P\left({\tau }^n|\theta \right)& & 【通过采样来估计\sum _{\tau }P(\tau |\theta )】\\ & =\frac{1}{N}\sum _{n=1}^{N}R\left({\tau }^n\right)\sum _{t=1}^{T_n}\nabla \log p\left(a_t^n|s_t^n,\theta \right)& & 【将\nabla \log P(\tau |\theta )代入】\\ & =\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}R\left({\tau }^n\right)\nabla \log p\left(a_t^n|s_t^n,\theta \right)& & \end{array}$$

为什么要使用对数呢？
除了前边提到的求导形式简单之外，还有一个理由——首先考虑原始的$$\nabla p\left(a_t^n|s_t^n,\theta \right)$$，
假设某种相对极端的情况，在一个片段中频繁采取动作a，那么在训练时会倾向于增加动作a的概率，即使动作b的奖励要高于动作a（但动作b的采用概率很低），这显然是不合理的，而按照前述，对数形式有
$$\log p\left(a_t^n|s_t^n,\theta \right)=\frac{\nabla p\left(a_t^n|s_t^n,\theta \right)}{p\left(a_t^n|s_t^n,\theta \right)}$$
这相当于用概率$$p\left(a_t^n|s_t^n,\theta \right)$$对原始的梯度$$\nabla p\left(a_t^n|s_t^n,\theta \right)$$做了规范化，从而避免了前边提到的极端情况。

两点改进

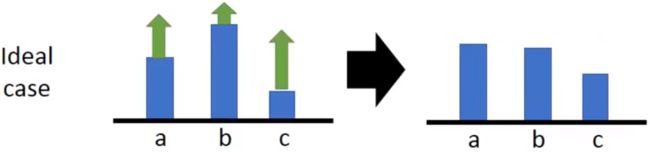
接下来我们看看$$R\left({\tau }^n\right)$$，有些任务可能并没有惩罚，也就是$$R\left({\tau }^n\right)\ge 0$$；即使任务有惩罚，但也有可能出现一个片段中所有奖励都是正值的情况，那么此时所有采样涉及的动作概率都会增加——但不用担心，由于所有动作的概率之和约束为1，所以概率“增加”较少的动作会被其他同样“增加”概率的动作挤兑，实际上概率是下降了。

但这只考虑了大家都被采样到的情况，假如有某个动作很倒霉，它在当前片段中一次都没有被采样，但它的概率依旧被降低了，这明显是不合理的。

所以我们可以为奖励引入一个baseline，让reward有正有负，从而缓解这样的问题。
$$\nabla {\bar{R}}_{\theta }\approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}\left(R\left({\tau }^n\right)-b\right)\nabla \log p\left(a_t^n|s_t^n,\theta \right)$$
baseline可以手工设计；也可以取奖励的期望，即$$b=E[R(\tau )]$$

再来讨论权重$$\left(R\left({\tau }^n\right)-b\right)$$的合理性。
考虑一个很小的片段$$\tau =\{(s_1,a_1,+5),(s_2,a_2,0),(s_3,a_3,-2)\}$$，可以算出它的奖励为$$R(\tau )=+3$$，这样一来$$\nabla \log p\left(a_1|s_1,\theta \right),\nabla \log p\left(a_2|s_2,\theta \right),\nabla \log p\left(a_3|s_3,\theta \right)$$的权重都是+3。可是总奖励$$R(\tau )$$的正值贡献主要来源于$${\tau }_1=(s_1,a_1,+5)$$，但我们又以相同的力度鼓励$${\tau }_2=(s_2,a_2,0)$$甚至$${\tau }_3=(s_3,a_3,-2)$$，这显然是有问题的。更合理的做法应当是统计当前阶段之后的奖励之和来作为自己的权重，而不是整个片段的总奖励，也即
$$R({\tau }_t^n)=\sum _{t^{\prime }=t}^{T_n}{r}_{t^{\prime }}^n$$
而且，为了鼓励尽早取得奖励（或者反过来说，为了减弱遥远未来的奖励的重要性），可以引入一个超参数折扣因子（discount factor）$$\gamma$$，奖励值进一步改造为
$$R({\tau }_t^n)=\sum _{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n,\gamma <1$$
最终变为
$$\begin{array}{rl}\nabla {\bar{R}}_{\theta }& \approx \frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}\left(R\left({\tau }_t^n\right)-b\right)\nabla \log p\left(a_t^n|s_t^n,\theta \right)\\ & =\frac{1}{N}\sum _{n=1}^N\sum _{t=1}^{T_n}\left(\sum _{t^{\prime }=t}^{T_n}{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}^n-b\right)\nabla \log p\left(a_t^n|s_t^n,\theta \right),\gamma <1\end{array}$$
事实上，$$\left(R\left({\tau }_t^n\right)-b\right)$$这一项被称为Advantage Function，记为$$A^{\theta }(s_t,a_t)$$，甚至可以训练一个critic来替代这里的手工设计，也即之后会讲的Value-based方法。

Off-Policy

如果用于采样的模型跟实际训练的模型是同一个模型，则称为On-Policy；如果不是同一个模型，则称为Off-Policy。为什么好好的不用同一个模型呢？这是因为我们可以用之前的模型进行采样获得很多数据，而用这些数据来做多次迭代，每迭代一定部署后再用训练模型的参数去更新采样模型，从而有效加快强化学习的训练过程。

分布修正

由于经过迭代，采样的模型的采样结果跟实际训练的模型的采样是会有差距的，因此需要引入一些措施来修正。
原始的梯度为
$$\nabla {\bar{R}}_{\theta }=E_{\tau \sim p_{\theta }(\tau )}\left[R(\tau )\nabla \log p_{\theta }(\tau )\right]$$
记训练模型的样本分布、采样模型的样本分布分别为$$p(x),q(x)$$
$$\begin{array}{rl}{E}_{x\sim p}[f(x)]& =\int f(x)p(x)dx\\ & =\int f(x)\frac{p(x)}{q(x)}q(x)dx\\ & =E_{x\sim q}[f(x)\frac{p(x)}{q(x)}]\end{array}$$
修正后的梯度可以表示为
$$\nabla {\bar{R}}_{\theta }=E_{\tau \sim p_{{\theta }^{\prime }}(\tau )}\left[\frac{p_{\theta }(\tau )}{p_{{\theta }^{\prime }}(\tau )}R(\tau )\nabla \log p_{\theta }(\tau )\right]$$
也即用$${\pi }_{{\theta }^{\prime }}$$采样的数据来训练$${\pi }_{\theta }$$，并且给奖励乘以一个$$\frac{p_{\theta }(\tau )}{p_{{\theta }^{\prime }}(\tau )}$$重要性因子作为修正（称为Importance Sample），修正后的梯度，可以保证采样数据的样本上期望是一致的。
展开来的话
$$\begin{array}{rl}\nabla {\bar{R}}_{\theta }& =E_{\tau \sim p_{{\theta }^{\prime }}(\tau )}\left[\frac{p_{\theta }(\tau )}{p_{{\theta }^{\prime }}(\tau )}R(\tau )\nabla \log p_{\theta }(\tau )\right]\\ & =E_{\left(s_t,a_t\right)\sim {\pi }_{\theta }}\left[A^{\theta }\left(s_t,a_t\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)\right]\\ & =E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{P_{\theta }\left(s_t,a_t\right)}{P_{{\theta }^{\prime }}\left(s_t,a_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)\right]\\ & =E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}\frac{p_{\theta }\left(s_t\right)}{p_{{\theta }^{\prime }}\left(s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)\right]\\ & (...\frac{p_{\theta }\left(s_t\right)}{p_{{\theta }^{\prime }}\left(s_t\right)}的实际值不好获得，但一般认为环境是\theta 无关的，所以不妨假设其值为1...)\\ & =E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\nabla \log p_{\theta }\left(a_t^n|s_t^n\right)\right]\end{array}$$
根据$$\nabla f(x)=f(x)\nabla \log f(x)$$可以由梯度反推出目标函数
$$J^{{\theta }^{\prime }}(\theta )=E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\right]$$

有了修正，是不是就可以为所欲为了呢？其实也不是，从方差上看
$${\mathrm{Var}}_{x\sim p}[f(x)]=E_{x\sim p}\left[f(x{)}^2\right]-{\left(E_{x\sim p}[f(x)]\right)}^2$$
而
$$\begin{array}{rl}{\mathrm{Var}}_{x\sim q}\left[f(x)\frac{p(x)}{q(x)}\right]& =E_{x\sim q}\left[{\left(f(x)\frac{p(x)}{q(x)}\right)}^2\right]-{\left(E_{x\sim q}\left[f(x)\frac{p(x)}{q(x)}\right]\right)}^2\\ & =E_{x\sim q}\left[f(x{)}^2\frac{p(x)}{q(x)}\frac{p(x)}{q(x)}\right]-{\left(E_{x\sim p}\left[f(x)\right]\right)}^2\\ & =E_{x\sim p}\left[f(x{)}^2\frac{p(x)}{q(x)}\right]-{\left(E_{x\sim p}\left[f(x)\right]\right)}^2\end{array}$$
显然方差是不完全相同的，而且随着$$p(x),q(x)$$差异变大，方差的差异也会随之变大。
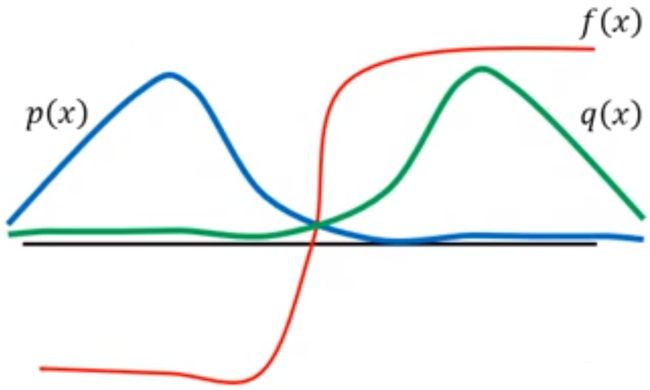
举个直观点的例子，

因为$$p(x)$$在左半部分概率比较高，而且这部分$$f(x)<0$$，显然$$E_{x\sim p}[f(x)]$$是负数；
因为$$q(x)$$在右半部分概率比较高，所以有可能采样点都在右侧，此时$$E_{x\sim q}[f(x)\frac{p(x)}{q(x)}]\approx \frac{1}{N}\sum _{i=1}^{N}f(x_i)\frac{p(x_i)}{q(x_i)}$$算出来却是正数，这下可差得远了。

所以需要采取一些额外措施，来避免$$p(x),q(x)$$相差太大。

TRPO和PPO

原始的目标函数为
$$J^{{\theta }^{\prime }}(\theta )=E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\right]$$

**信任区域策略优化（Trust Region Policy Optimization, TRPO）**对目标函数做了一些约束，要求采样模型和训练模型在输出分布上的差异不能太大，
$$J_{TRPO}^{{\theta }^{\prime }}(\theta )=E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\right],KL\left(\theta ,{\theta }^{\prime }\right)<\delta$$
注意：这里$$KL(\theta ,{\theta }^{\prime })$$指的不是参数分布的KL散度，而是模型输出的分布，下文的PPO也是如此。
但带条件约束的目标函数在实际操作中并不好处理；

邻近策略优化（Proximal Policy Optimization, PPO）将该约束体现在了计算公式中去，直接用它来做惩罚，
$$J_{PPO}^{{\theta }^{\prime }}(\theta )=E_{\left(s_t,a_t\right)\sim {\pi }_{{\theta }^{\prime }}}\left[\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^{\prime }}\left(a_t|s_t\right)}{A}^{{\theta }^{\prime }}\left(s_t,a_t\right)\right]-\beta KL\left(\theta ,{\theta }^{\prime }\right)$$
同时也有一种更简洁的形式，通常称为PPO2，
$$J_{PPO2}^{{\theta }^k}(\theta )=\sum _{\left(s_t,a_t\right)}\min \left(\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)}{A}^{{\theta }^k}\left(s_t,a_t\right),\text{ clip }\left(\frac{p_{\theta }\left(a_t|s_t\right)}{p_{{\theta }^k}\left(a_t|s_t\right)},1-\epsilon ,1+\epsilon \right)A^{{\theta }^k}\left(s_t,a_t\right)\right)$$
看起来复杂，实际上是加了一个自适应的一个权重，