Leetcode刷题：剑指offer【面试题04 二维数组中的查找】

【面试题04】二维数组中的查找

难度： 简单
要求： 在二维数组中查找是否存在target
限制： 0 <= n <= 1000，0 <= m <= 1000

在一个 n * m 的二维数组中，每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

Leetcode题目对应位置： 面试题04：二维数组中的查找

思路一：暴力法

直接每行每列循环查找，没有利用到题目中给出的数组特性，不是很推荐。

时间复杂度：O(n * m)，嵌套的双重循环，n 行 m 列。
空间复杂度：O(1)

class Solution:
    def findNumberIn2DArray(self, matrix, target) -> bool:
        for i in matrix:
            for j in i:
                if target == j:
                    return True
        return False

思路二：二分法查找

也是一个比较基本的思路，由于数组递增的性质，可以知道只要某一列第一个数大于 target 或某一列最后一个数小于 target，那么 target 肯定不可能在该列里。所以有代码逻辑：

1）循环遍历数组每一列，若该列第一个数或最后一个数就是 target，则直接 return True；
2）否则判断该列第一个数是否小于 target 且 最后一个数是否大于 target，这两个条件同时满足再对该列进行二分查找。

时间复杂度：O(mlogn)最坏情况下每一列都要二分查找
空间复杂度：O(1)

class Solution:
    def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
        if not matrix: return False
        col = len(matrix[0])
        idx = 0
        for i in range(col):
            if matrix[0][i] == target or matrix[len(matrix)-1][i] == target: 
                return True
            elif matrix[0][i] < target and matrix[len(matrix)-1][i] > target:
                idx = self.biSearch(matrix, i, target)
            if idx:
                return True
        return False

    def biSearch(self, matrix, column, target):
        low = 0
        high = len(matrix) - 1
        while low <= high:
            mid = int((high - low) / 2) + low
            if matrix[mid][column] < target:
                low = mid + 1
            elif matrix[mid][column] > target:
                high = mid - 1
            else: return mid
        return 0

其实在排除列的过程中，也可以使用二分查找，不需要一个一个判断的，就是从右向左找矩阵第一行第一个等于或小于 target 的数，确定一个索引范围，然后从左向右找矩阵最后一行第一个等于或大于 target 的数，再确定一个索引范围，两个范围结合起来，对这些列进行二分查找即可。这个解法纯属抛砖引玉，如果有时间各位大佬可以自己写，我真的是太懒啦…

思路三：二叉查找树 ⭐

根据数组所给特性，其实它就是个二叉查找树（Binary Search Tree）的变种。从右上角看，每个结点的左子树根节点必定小于它，右子树根节点必定大于它。那么根据二叉搜索树的查找方法，就有以下查找逻辑：

1）若查找的目标关键字值等于根节点的关键字值，查找成功。
2）否则，若查找的目标关键字值小于根节点的关键字值，则递归查找左子树，若查找的目标关键字值大于根节点的关键字值，则递归查找右子树。
3）若子树为空，则查找不成功。

根据这样的逻辑，如果数组中存在 target 值，则是肯定能找到，不会出现遗漏。

至于为什么这么做有一个很简单的逻辑，应该都能想得到，看矩阵第一行和最后一行的值：假设 target = 7
1）如果某列第 1 个的值 > target 值，那么就没必要再往下找了，因为数组特性就是行和列都是递增的，第一个值已经大于了 target，那么再往下根本不可能出现 target，比如下面矩阵的第 3、第 4 列，第一个值分别是 8 和 9，那么下面肯定不会有 7，排除这两列。所以在以右上角为根节点的例子里，9 -> 8 -> 2。
2）同样地，如果某列最后一个值 < target 值，那么也没必要往上找了，因为上面元素值只会更小，比如下面矩阵的第 1 列，最后一个值是 6，小于 target 7，故排除这一列。所以在以左下角为根节点的例子里，6 -> 8，而不是 6 -> 4。

① 以右上角为根节点：

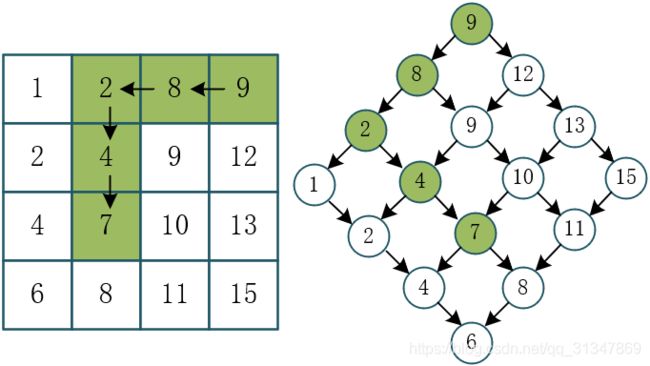
① 以左下角为根节点：

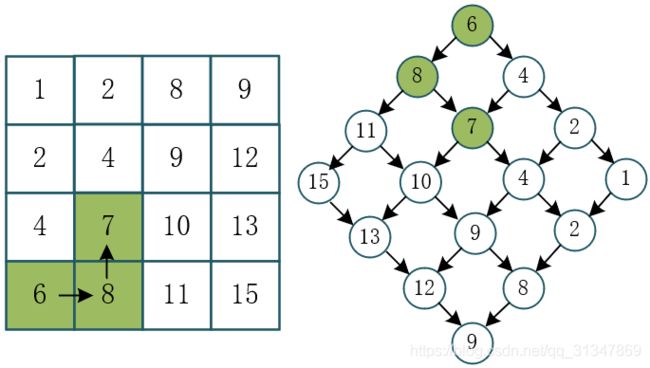
其实不管从右上角还是从左下角，核心思想都是为了在每轮比较时排除掉一行或一列，找到“应该走的下一步”。这样的好处就是降低了时间复杂度。

时间复杂度：O(n+m)，最坏情况下，行标增加 n 次，列标减少 m 次，循环体最多执行 m + n 次。
空间复杂度：O(1)

第一种： 从右上角向下遍历

1）右上角元素索引为 [i, j] = [0, len(matrix[0]) - 1]，与 target 进行对比，若恰好相等则 return True；
2）否则，若 matrix[i, j] > target，则列索引减 1，j --；若 matrix[i, j] < target，则行索引加 1，i ++；
3）若行或者列索引越界，表示矩阵中无 target，返回 false。

# 从右上角开始查找
class Solution:
    def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
        if not matrix: return False
        i, j = 0, len(matrix[0]) - 1
        while i < len(matrix) and j >= 0:
            if matrix[i][j] > target: j -= 1
            elif matrix[i][j] < target: i += 1
            else: return True
        return False

第二种： 从左下角向上遍历

1）左下角元素索引为 [i, j] = [len(matrix) - 1, 0]，与 target 进行对比，若恰好相等则 return True；
2）否则，若 matrix[i, j] > target，则行索引减 1，i --；若 matrix[i, j] < target，则列索引加 1，j ++；
3）若行或者列索引越界，表示矩阵中无 target，返回 false。

# 从左下角开始查找
class Solution:
    def findNumberIn2DArray(self, matrix: List[List[int]], target: int) -> bool:
        i, j = len(matrix) - 1, 0
        while i >= 0 and j < len(matrix[0]):
            if matrix[i][j] > target: i -= 1
            elif matrix[i][j] < target: j += 1
            else: return True
        return False

需要注意的几个细节问题：

1）若从右上角开始查找，需要先判断数组是否为空的一维数组 []，否则在计算 len(matrix[0]) 时会报错：索引越界
2）len(matrix) 计算的是数组的行数，len(matrix[0]) 计算的是数组的列数，相当于取 matrix 第一行后计算元素个数。
3）不能选择以左上角或右下角的元素为根节点，这样无法缩小查找范围。

---

参考资料：
[1] LeetCode 面试题04：数组中重复的数字
[2] LeetCode题解 - 作者：Krahets
[3] 剑指 offer 第二版