42. 接雨水(难度:困难)
42. 接雨水(难度:困难)
题目链接:https://leetcode-cn.com/problems/trapping-rain-water/
题目描述:
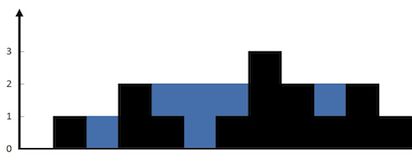
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。 感谢 Marcos 贡献此图。
示例:
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6
解法一:动态规划法
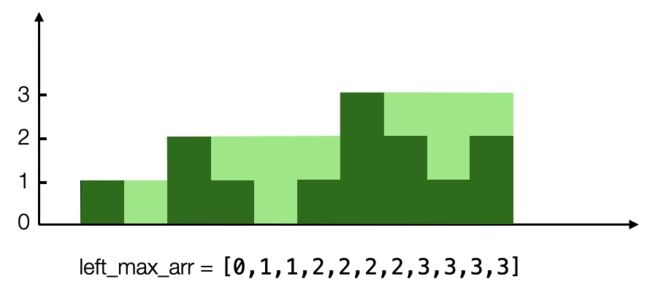
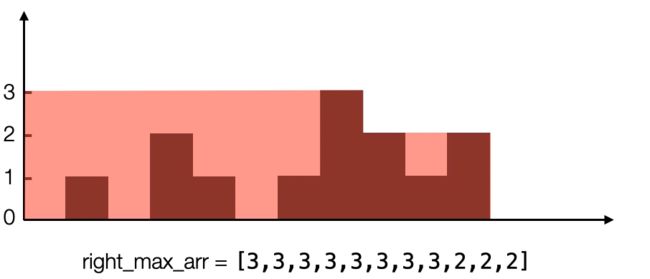
我们可以,计算每一个位置,对应的左边最大值和右边最大值,即从这个位置,向左看,找到最高块的高度,设为他的左边最大值;同理,向右看,找到右边的最高快的高度,设为他的右边最大值。
左边最大值:
右边最大值:
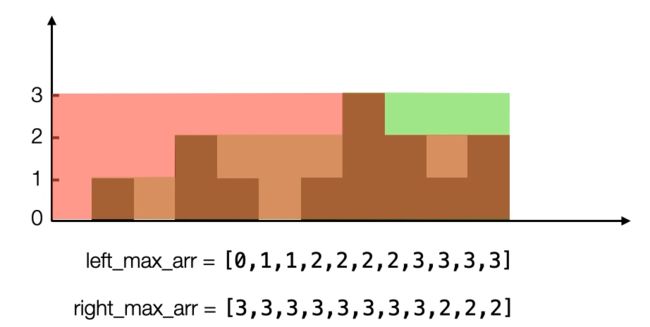
然后,我们可以计算每块低洼处可以存放的水,就是该位置的左边最大值和右边最大值两个值中的较小值,然后再减去该位置块的高度,就是此位置低洼处的存水量,然后将每个位置的存水量累加,就是最后的结果。
如上图:
-
在下标为0,左右最大值的较小值为0,此处高度为0,相减得此处的存水量为0;
-
在下标为1,左右最大值的较小值为1,此处高度为1,相减得此处的存水量为0;
-
在下标为2,左右最大值的较小值为1,此处高度为0,相减得此处的存水量为1;
-
在下标为3,左右最大值的较小值为2,此处高度为2,相减得此处的存水量为0;
………………
代码:
class Solution {
public int trap(int[] height) {
if(height.length == 0) return 0;
int result = 0;
int len = height.length;
int[] lMax = new int[len];
int[] rMax = new int[len];
lMax[0] = height[0];
rMax[len-1] = height[len-1];
for(int i = 1;i<len;i++) {
lMax[i] = Math.max(lMax[i-1], height[i]);
}
for(int i = len-2;i>=0;i--) {
rMax[i] = Math.max(rMax[i+1], height[i]);
}
for(int i = 0;i<len;i++) {
result += Math.min(lMax[i], rMax[i]) - height[i];
}
return result;
}
}