力扣——48.旋转图像(中等难度)——仅仅考验你的数学思维
力扣——48.旋转图像
- 一、算法目录合集
- 1.地址
- 2.说明
- 二、题目说明
- 1.题干
- 2.原地址
- 三、实现步骤
- 1.思路分析
- 1.1.旋转
- 1.2.转化问题
- 1.3.简化问题
- 1.4.具体步骤
- ① 特殊情况分析
- ② 常规分析
- ③ 分类分析
- ④ 简化代码
- 2.代码实现
- 2.1 方法代码
- 2.2 测试部分代码
- 2.3 耗用资源情况
- 四、官方题解
- 1.原地址
- 2.方法一——转置加翻转
- 思路分析
- 代码实现（Java）
- 复杂度
- 3.方法二——旋转四个矩形
- 思路分析
- 代码实现（Java）
- 复杂度
- 4.方法三——在单次循环中旋转 4 个矩形
- 思路分析
- 代码实现（Java）
- 复杂度
一、算法目录合集
1.地址
算法目录合集
2.说明
该地址指向所有由本人自己所经历的算法习题(也有可能仅仅是一个入门的案例或者是经典案例)，仅仅为我做过而且比较有意思的，也许还会有一些我自己想出来的，出于兴趣写在这里,具体格式我会在下面列明，总目录也会在这里出现，方便查阅以及自己进行复习回顾。
二、题目说明
1.题干
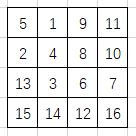
给定一个 n × n 的二维矩阵表示一个图像。将图像顺时针旋转 90 度。
- 说明：
你必须在原地旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
- 示例 1:
给定 matrix =
[1,2,3],
[4,5,6],
[7,8,9]
原地旋转输入矩阵，使其变为:
[7,4,1],
[8,5,2],
[9,6,3]
- 示例 2:
给定 matrix =
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
原地旋转输入矩阵，使其变为:
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
2.原地址
48.旋转图像
三、实现步骤
1.思路分析
大家首先看到这个，有的会不管要求，上来一通操作，像下图一样，先定义一个新的矩阵，然后遍历新的矩阵，把图壹的各个元素按照颜色直接打在图贰上，然后直接再遍历图壹，把图贰复制回来即可。
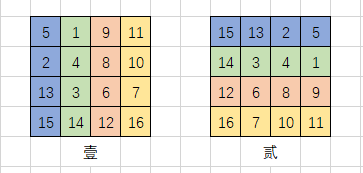
很遗憾地告诉您，稍微思路偏了一点儿，因为题目要求，请不要使用另一个矩阵来旋转图像。这就要求我们需要在现在这个矩阵里面直接操作。
如果抛弃这种引入一个矩形的方法，那么可以尝试引入多个数组，来存放上图中的同色条块，等取出所有值之后，最后以此再存回图壹。对于这种操作，我只想说这和定义一个矩阵有本质上的区别吗？
还是请大家不要取巧，按照正常流程来进行分析：
1.1.旋转
搞清楚什么是旋转，怎么去旋转，题目中已然给了要求，顺时针旋转 90 度，也就是说把下图中左边的这么一个玩意儿变成右图的这么一个玩意儿，只不过数字是正着的，就这么简单。
乱糟糟的一堆数字找不到一丝丝规律，看着烦不烦？烦，就得学会将表面的问题转化成实质的问题，也就是看到问题的本质，这个问题的本质就是并不是将11（右上角的数字）变成了5（左上角的数字），而是把5这个位置的数字挪到了11这个位置，和5，和11这俩数字没有1毛钱的关系，哪怕是个鸡蛋鸭蛋也得挪过去
1.2.转化问题
上面说的很清楚，位置，在数学上体现就是坐标系，而在这个双数组的矩阵中的表现，就是索引。
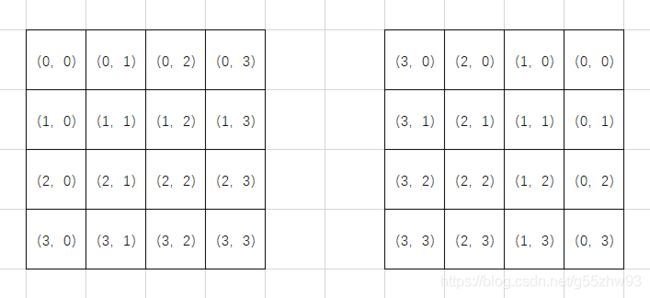
这不就转化成了我们非常熟悉的语言了？无论是用数学的思想还是计算机的思想，都可以直接解决问题。
1.3.简化问题
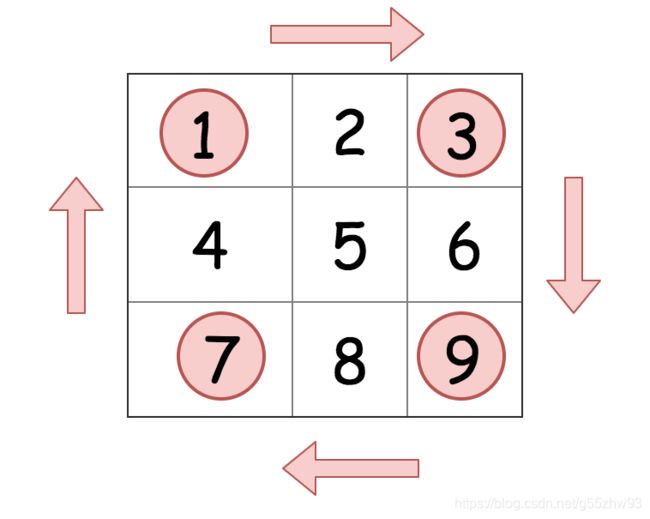
有人就说了，不行，你这样我还是看不出来咋搞，我只有用手能转动，代码我实现不了。那就继续看看：我们最终实现的是这个样子（既然是顺时针旋转，那么不如以最中间为轴，也就像下图一样）。
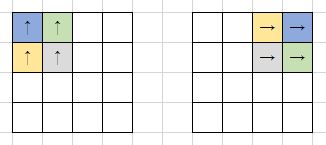
旋转不会，我们就继续分割问题，如何利用翻转表现出旋转？请看下图：
图壹是原图，实现以红线为轴进行轴对称变换成为图贰，图贰再以红线为轴，进程轴对称变换成为图叁。两个简单步骤就可以实现了顺时针旋转。
表现在数学的思想上，就是把左上角看作是原点，右和下为正方向，那么我们只需要做的变化就是①x不变，y变为2×对称轴-y；②xy互换。
这样，就得到了我们最核心的代码：
private void change(int[][] matrix, int len, int i, int j) {
int ex;
ex = matrix[i][j];
matrix[i][j] = matrix[len - j][i];
matrix[len - j][i] = matrix[len - i][len - j];
matrix[len - i][len - j] = matrix[j][len - i];
matrix[j][len - i] = ex;
}
这里有个非常重要的一点：我们在旋转的时候是吧整个矩阵分成了四块，单独将
第三块挪到了第四块上面
第二块挪到了第三块上面
第一块挪到了第二块上面
第四块挪到了第一块上面
所以，在循环遍历的时候，我们只需要遍历每一个数组的一半，即可完成整个图形的旋转。
比如：（0，0）转到（0，3），就是先变成（3，0），再变成（0，3）。核心方法既然得出来了，那么就是简单地规划实现具体步骤了。
1.4.具体步骤
① 特殊情况分析
分析问题先去分析特例：极大值或者极小值，这两个值一般是需要特殊定义的，对于本题来说，极大值无非是图非常大，是不需要我们做过多的操作的，主要是极小值，至于这个值有多小呢？“0”即可。
在数组为null或者是一个空数组的时候“{}”，特殊定义一下就好了，于是第一步就是：
if (matrix == null || matrix.length == 0){
return;
}
② 常规分析
对于后续的操作，肯定是需要一个一般步骤的，那就不用管其他的，先按照咱们上边的思路进行书写（int n = 数组长的一半，这个原因在上面已经说了）：
if (matrix == null || matrix.length == 0){
return;
}
int n = matrix.length / 2;
int len = matrix.length -1;
int ex = 0;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
ex = matrix[i][j];
matrix[i][j] = matrix[len - j][i];
matrix[len - j][i] = matrix[len - i][len - j];
matrix[len - i][len - j] = matrix[j][len - i];
matrix[j][len - i] = ex;
}
}
这就是一般步骤了，对于咱们的这个4×4的矩阵是完全没问题的，到这儿已经成功了一半。下面就是另外一种可能了，请看下图：
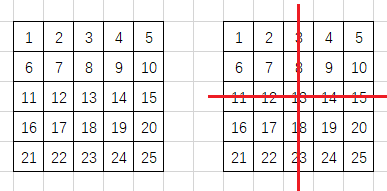
对于5×5的矩阵怎么解决呢？
③ 分类分析
如果选取了一半，那包含了边，在按照以上方法操作了以后，红线所在的那些数字可被操作了不止一次了，那肯定得不到我们想要的数据了，解决这个问题有两种方法一个是只移动左上角的矩形，即1，2，3，6，7，8这6个数字所在的边，还有一种方法就是暂时先不管中间的，依旧按照原来的方法先旋转，然后对中轴进行单独操作，就像下图,操作彩色部分:
于是就有了以下代码
if (matrix == null || matrix.length == 0){
return;
}
int len = matrix.length -1;
int ex = 0;
int n;
if (matrix.length % 2 == 0){
n = matrix.length / 2;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
ex = matrix[i][j];
matrix[i][j] = matrix[len - j][i];
matrix[len - j][i] = matrix[len - i][len - j];
matrix[len - i][len - j] = matrix[j][len - i];
matrix[j][len - i] = ex;
}
}
}else {
n = matrix.length / 2;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
ex = matrix[i][j];
matrix[i][j] = matrix[len - j][i];
matrix[len - j][i] = matrix[len - i][len - j];
matrix[len - i][len - j] = matrix[j][len - i];
matrix[j][len - i] = ex;
}
}
//处理中轴
n = matrix.length / 2 ;
for (int i = 0; i < n; i++) {
int ex;
ex = matrix[i][n];
matrix[i][n] = matrix[len - n][i];
matrix[len - n][i] = matrix[len - i][len - n];
matrix[len - i][len - n] = matrix[n][len - i];
matrix[n][len - i] = ex;
}
}
④ 简化代码
很容易看出上面代码有很多重复的部分，所以抽取方法
private void change(int[][] matrix, int len, int i, int j) {
int ex;
ex = matrix[i][j];
matrix[i][j] = matrix[len - j][i];
matrix[len - j][i] = matrix[len - i][len - j];
matrix[len - i][len - j] = matrix[j][len - i];
matrix[j][len - i] = ex;
}
将方法整合到完整代码里即可。
2.代码实现
2.1 方法代码
class Solution48 {
public void rotate(int[][] matrix) {
if (matrix == null || matrix.length == 0){
return;
}
int n;
int len = matrix.length -1;
if (matrix.length % 2 == 0){
n = matrix.length / 2;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
change(matrix, len, i, j);
}
}
}else {
n = matrix.length / 2;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
change(matrix, len, i, j);
}
}
//处理中轴
n = matrix.length / 2 ;
for (int i = 0; i < n; i++) {
change(matrix, len, i, n);
}
}
}
private void change(int[][] matrix, int len, int i, int j) {
int ex;
ex = matrix[i][j];
matrix[i][j] = matrix[len - j][i];
matrix[len - j][i] = matrix[len - i][len - j];
matrix[len - i][len - j] = matrix[j][len - i];
matrix[j][len - i] = ex;
}
}
2.2 测试部分代码
这里随便定义一个随便看看就好了
public class Test48Middle {
public static void main(String[] args) {
Solution48 s = new Solution48();
int[][] arrNull = null;
int[][] arr = new int[][]{};
int[][] arr1 = new int[][]{{1}};
int[][] arr2 = new int[][]{{1,2},{3,4}};
int[][] arr3 = new int[][] {{1,2,3},{4,5,6},{7,8,9}};
int[][] arr4 = new int[][] {{5,1,9,11},{2,4,8,10},{13,3,6,7},{15,14,12,16}};
int[][] arr5 = new int[][] {{1,2,3,4,5},{6,7,8,9,10},{11,12,13,14,15},{16,17,18,19,20},{21,22,23,24,25}};
s.rotate(arr5);
for (int i = 0; i < arr5.length; i++) {
for (int i1 = 0; i1 < arr5[i].length; i1++) {
System.out.println(arr5[i][i1]);//懒得输出成矩阵了，就这么看吧
}
}
}
}
2.3 耗用资源情况
之所以耗用时间是100%是因为人家没统计(自爆求好感)
四、官方题解
1.原地址
力扣官方答疑戳这里
2.方法一——转置加翻转
思路分析
最直接的想法是先转置矩阵，然后翻转每一行。这个简单的方法已经能达到最优的时间复杂度O(N2 )。
代码实现（Java）
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
// transpose matrix
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
int tmp = matrix[j][i];
matrix[j][i] = matrix[i][j];
matrix[i][j] = tmp;
}
}
// reverse each row
for (int i = 0; i < n; i++) {
for (int j = 0; j < n / 2; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[i][n - j - 1];
matrix[i][n - j - 1] = tmp;
}
}
}
}
复杂度
时间复杂度：
O(N2 )。
空间复杂度：
O(1)由于旋转操作是 就地 完成的。
3.方法二——旋转四个矩形
思路分析
方法 1 使用了两次矩阵操作，但是有只使用一次操作的方法完成旋转。
为了实现这一点，我们来研究每个元素在旋转的过程中如何移动。
这提供给我们了一个思路，将给定的矩阵分成四个矩形并且将原问题划归为旋转这些矩形的问题。
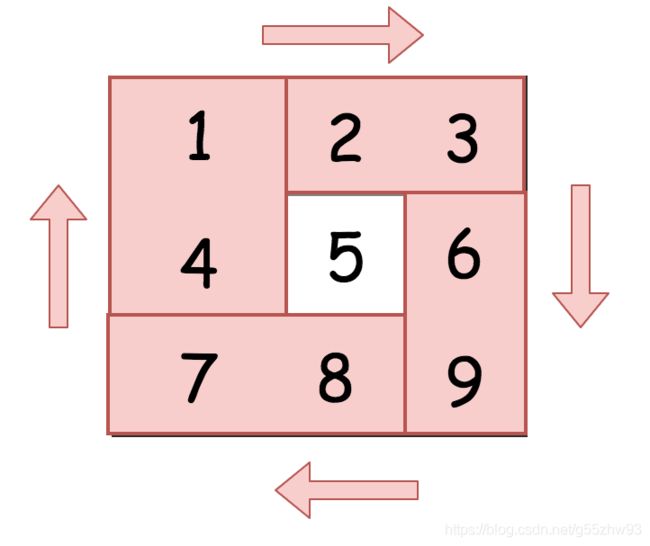
现在的解法很直接，可以在第一个矩形中移动元素并且在 长度为 4 个元素的临时列表中移动它们。
代码实现（Java）
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
// transpose matrix
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
int tmp = matrix[j][i];
matrix[j][i] = matrix[i][j];
matrix[i][j] = tmp;
}
}
// reverse each row
for (int i = 0; i < n; i++) {
for (int j = 0; j < n / 2; j++) {
int tmp = matrix[i][j];
matrix[i][j] = matrix[i][n - j - 1];
matrix[i][n - j - 1] = tmp;
}
}
}
}
复杂度
时间复杂度：
O(N2 )是两重循环的复杂度。
空间复杂度：
O(1)由于我们在一次循环中的操作是 就地 完成的，并且我们只用了长度为 4 的临时列表做辅助。
4.方法三——在单次循环中旋转 4 个矩形
思路分析
该想法和方法 2 相同，但是所有的操作可以在单次循环内完成并且这是更精简的方法。
代码实现（Java）
class Solution {
public void rotate(int[][] matrix) {
int n = matrix.length;
for (int i = 0; i < (n + 1) / 2; i ++) {
for (int j = 0; j < n / 2; j++) {
int temp = matrix[n - 1 - j][i];
matrix[n - 1 - j][i] = matrix[n - 1 - i][n - j - 1];
matrix[n - 1 - i][n - j - 1] = matrix[j][n - 1 -i];
matrix[j][n - 1 - i] = matrix[i][j];
matrix[i][j] = temp;
}
}
}
}
复杂度
时间复杂度：
O(N2 )是两重循环的复杂度。
空间复杂度：
O(1)由于旋转操作是 就地 完成的。