最短距离问题（Floyed-Warshall算法）

题目链接：

https://begin.lydsy.com/JudgeOnline/problem.php?cid=1318&pid=10

Problem K: 最短路径问题

Time Limit: 1 Sec Memory Limit: 128 MB

Description

平面上有n个点（n<=100），每个点的坐标均在-10000~10000之间。其中的一些点之间有连线。若有连线，则表示可从一个点到达另一个点，即两点间有通路，通路的距离为两点间的直线距离。现在的任务是找出从一点到另一点之间的最短路径。

Input

共n+m+3行，其中:
第一行为整数n。
第2行到第n+1行（共n行），每行两个整数x和y，描述了一个点的坐标。
第n+2行为一个整数m，表示图中连线的个数。
此后的m行，每行描述一条连线，由两个整数i和j组成，表示第i个点和第j个点之间有连线。
最后一行：两个整数s和t，分别表示源点和目标点。

Output

仅一行，一个实数（保留两位小数），表示从s到t的最短路径长度。

Sample Input

5
0 0
2 0
2 2
0 2
3 1
5
1 2
1 3
1 4
2 5
3 5
1 5

Sample Output

3.41

HINT

题目分析:

1.引子

首先本题一看，就知道是最小路径问题，那么我们首先了解一下什么是带权图：
我们把边带有权值的图称为带权图。
摆上一张图：

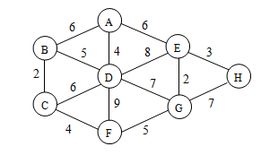
我们可以看到图中有许多点，且任两点之间会有不同的路径相连。最短路径就是指连接两点的这些路径中最短的一条。

2.解决方法

我们有四种算法可以有效解决这个问题，但有一点要特别注意，边的权值可以为负，当出现负边权时，有些算法就不再适用。
算法1：Floyed-Warshall算法 O(n^3)
算法2：Dijkstra算法 O(n^2)
算法3：Bellman-Ford算法 O(NE) [N为顶点数，E为边数]
算法3：Bellman-Ford算法 O(NE) [N为顶点数，E为边数]
算法4：SPFA算法 O(KE) [同3，但使用队列维护，优化算法]
奈何本蒟蒻只学了Floyed-Warshall算法 O(n^3)，所以这里不再赘述。
我们来看看算法的解释：
一、 作用：
1.求多源最短路径；
2.判断图中两点是否相连。
PS：算法较为简单，容易理解，但不适用数据规模很大的情况。
二、 实现方法：
设置f[i][j]为点i到j的最短距离，初始值设为INF，设置三层循环，分为d，i，j，则f[i][j] = min(f[i][j],f[i][d]+f[d][j])；
循环结束，则可求出各点到各点的最短距离。
看不懂没关系，其实一张图就能说明一切：

我们发现三点间各有联系，那么从1到2有两条路径：
1. 1 to 2：f[1][2]=6
2. 1 to 3 to 2 : f[1][3]+f[3][2]=3
很明显，从1到2的最短路径是2.
那么也就是说用路径2.来替代1.更新1到2的最短距离。
所以我们可以很清楚的发现：
不断地枚举中间点，算出出发点经中间点到结束点的距离来与原来f[i][j]的值进行比较。
那么思路也很清晰了，代码实现如下：

bool check(int x,int y,int z)
{
	return (x!=y)&&(y!=z)&&(x!=z)&&(f[x][z]+f[z][y]<f[x][y]);
}//判断函数，即出发点不能到自身且中间点不能与其他两点重合
而且最后要用比较小的数值来替代f[i][j]

for (int d=1;d<=n;d++)//Floyed-Warshall算法，枚举中间点
		for (int i=1;i<=n;i++)//枚举出发点
			for (int j=1;j<=n;j++)//枚举目的点
				if (check(i,j,d))//判断
					f[i][j]=f[i][d]+f[d][j];//更新最短距离

最终代码：

#include 
#include 
#include 
#pragma GCC optmize(2)
using namespace std;

int n,m,a,b,s,t;
int x[101],y[101];
double f[101][101];

bool check(int x,int y,int z)
{
	return (x!=y)&&(y!=z)&&(x!=z)&&(f[x][z]+f[z][y]<f[x][y]);
}

inline void read(int &x)//快读
{
	x=0;int f=1;char c=getchar();
	while (c<'0'||c>'9') {if (c=='-') f=~(f-1);c=getchar();}
	while (c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar();
	x*=f;
}

int main()
{
	read(n);
	for (int i=1;i<=n;i++)
		read(x[i]),read(y[i]);
	read(m);
	memset(f,0x7f,sizeof(f));
	//将所有边打上无限大，即默认任两点都无联系
	for (int i=1;i<=m;i++)
	{
		read(a),read(b);
		f[a][b]=f[b][a]=sqrt(pow(double(x[a]-x[b]),2)+pow(double(y[a]-y[b]),2));
		//勾股定理求两点距离，注意，此为无向图，所以a to b与b to a都要赋值
	}
	read(s),read(t);
	for (int d=1;d<=n;d++)
		for (int i=1;i<=n;i++)
			for (int j=1;j<=n;j++)
				if (check(i,j,d))
					f[i][j]=f[i][d]+f[d][j];
	//三层循环，不断用一个中间点去寻找最短距离
	printf("%.2f",f[s][t]);//输出限制，根据题意
	return 0;
}