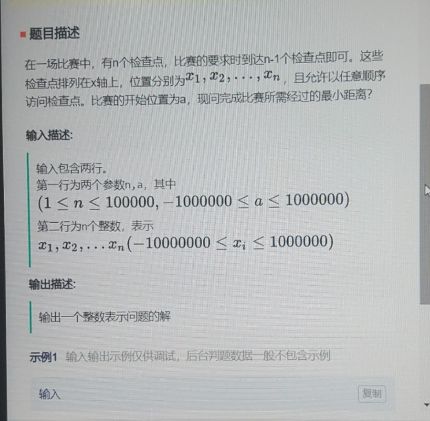
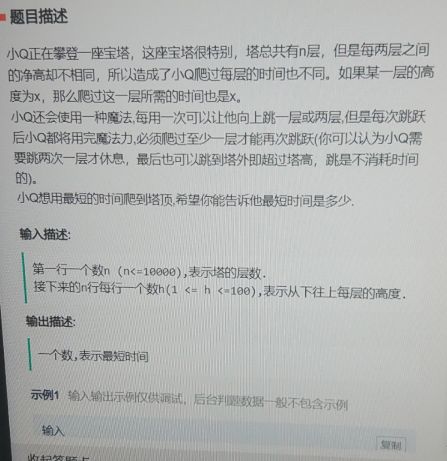
1. 题目一
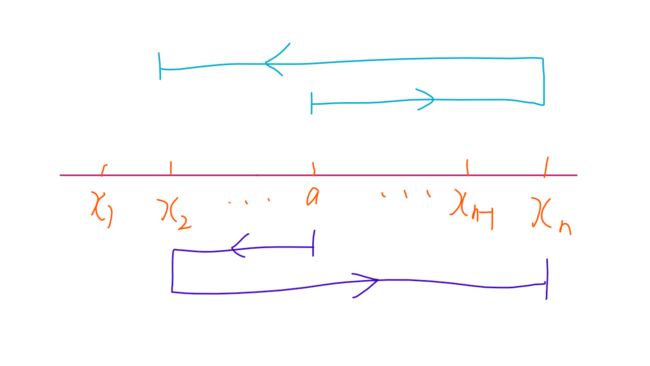
首先将数据排序,则两端的点距离最远肯定要舍弃一个,访问 \(n-1\) 个点只有两种情况,\(x_1 \to x_{n-1} 或者 x_2 \to x_{n}\)。假设访问的点是 \(x_2 \to x_{n}\),则又有下图两种访问顺序,先右后左或者先左后右,距离分别为 \(dis1 = 2 * (x_n - a) + (a - x_2)\) 和 \(dis2 = 2 * (a - x_2) + (x_n - a)\)。
因此,共计四个距离,选取最小的一个即可。
#include
#include
#include
#include
#include
using namespace std;
int main()
{
int n = 0;
int a = 0;
scanf("%d %d", &n, &a);
vector pos;
for(int i = 0; i < n; i++)
{
int temp;
scanf("%d", &temp);
pos.push_back(temp);
}
sort(pos.begin(), pos.end());
// 0 到 n-2 先左后右
int dis1 = 2 * abs(a - pos[0]) + abs(pos[n-2] - a);
// 0 到 n-2 先右后左
int dis2 = abs(a - pos[0]) + 2 * abs(pos[n-2] - a);
// 1 到 n-1 先左后右
int dis3 = 2 * abs(a - pos[1]) + abs(pos[n-1] - a);
// 1 到 n-1 先右后左
int dis4 = abs(a - pos[1]) + 2 * abs(pos[n-1] - a);
int result = INT_MAX;
result = min(result, dis1);
result = min(result, dis2);
result = min(result, dis3);
result = min(result, dis4);
cout << result << endl;
return 0;
} 2. 题目二
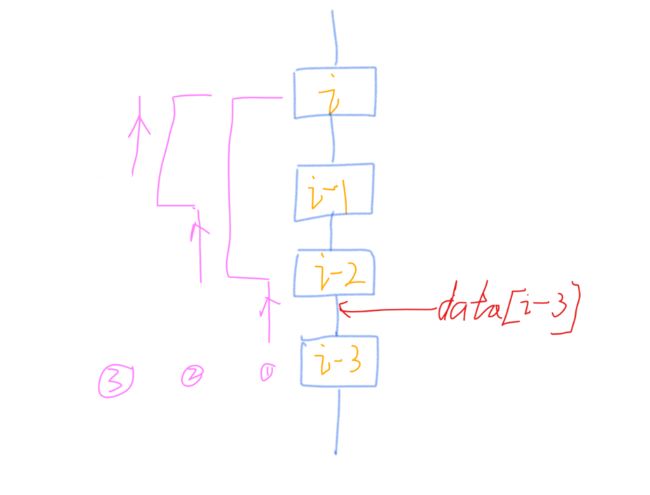
我们假设爬到第 \(i\) 层需要的最少时间为 \(S[i]\),那么我们有三种情况可以做到。
第一,从 \(i-2\) 层跳两层过来,根据题意,跳之前我们肯定爬过了一层(不可能连续跳两次),也就是从第 \(i-3\) 层爬到了第 \(i-2\) 层,然后再跳到第 \(i\) 层,这时候,需要的时间即为 \(S[i] = S[i-3]+data[i-3]\),注意此处,\(data[i-3]\)是数组的第 \(i-2\) 个元素,代表第 \(i-2\) 层的高度。
第二,从 \(i-1\) 层跳一层过来,也就是从第 \(i-2\) 层爬到了第 \(i-1\) 层,然后再跳到第 \(i\) 层,这时候,需要的时间即为 \(S[i] = S[i-2]+data[i-2]\)。
第三,从 \(i-1\) 层直接爬到第 \(i\) 层,这时候,\(S[i] = S[i-1]+data[i-1]\)。
所以,\(S[i]\) 即为以上三种情况的最小值。
\[S[i] = \begin{cases} min(S[i-3]+data[i-3], S[i-2]+data[i-2], S[i-1]+data[i-1]), \quad i >= 3 \\ 0, \quad i <3 \end{cases}\]
#include
#include
#include
#include
using namespace std;
int main()
{
int result = 0;
int n;
scanf("%d", &n);
int data[n];
for(int i = 0;i < n; i++) scanf("%d", &data[i]);
int dp[n+1];
dp[0] = 0;
dp[1] = 0;
dp[2] = 0;
for (int i = 3; i < n + 1; ++i)
{
dp[i] = min(min(dp[i-3] + data[i-3], dp[i-2] + data[i-2]),dp[i-1] + data[i-1]);
}
cout << dp[n];
return 0;
} 3. 题目三
借助队列来实现即可。
#include
#include
using namespace std;
int main()
{
int n = 0;
scanf("%d", &n);
queue q;
for (int i = 1; i <= n; i++) q.push(i);
while (q.size() != 1)
{
printf("%d ", q.front());
q.pop();
q.push(q.front());
q.pop();
}
printf("%d", q.front());
return 0;
} 4. 题目四
待定
5. 题目五
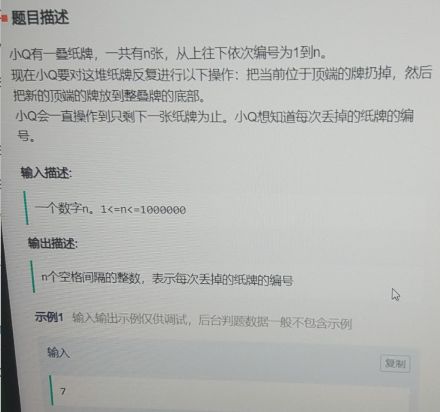
小 Q 得到了一个长度为 \(n\) 的序列 \(A\),\(A\) 中的数各不相同。对于 \(A\) 中的每一个数 \(A_i(2\leqslant i\leqslant n)\) ,求 \(min|A_i-A_j|, j < i\) 以及令上式取得最小值的下标 \(j\) 。若最小值点不唯一,则选择较小的那个。
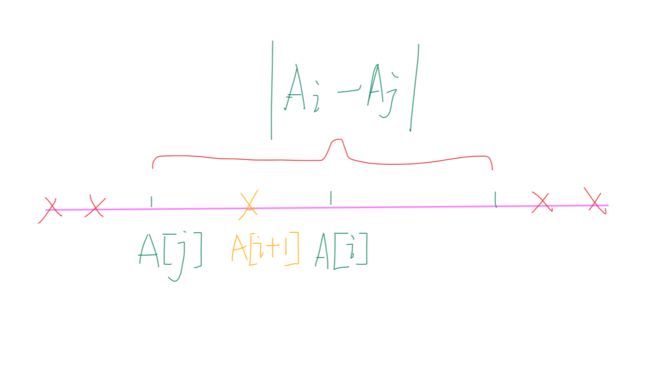
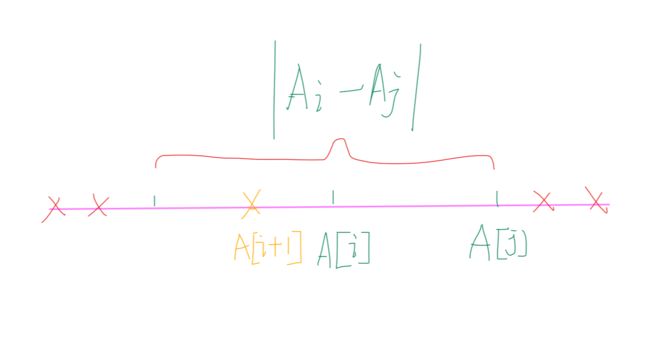
假设 \(A[j]\) 和 \(A[i]\) 的绝对值最小,则 \(A[i]\) 左边其余的数据分布在大括号两边,如下图所示。
- 若 \(A[j] \leqslant A[i+1] \leqslant A[i]\),则排除掉左右两边的点;
- 若 \(A[i+1] < A[j] \leqslant A[i]\),则排除掉右边的点;
- 若 \(A[j] \leqslant A[i] < A[i+1]\),则排除掉左边的点;
- 若 \(A[i] \leqslant A[i+1] \leqslant A[j]\),则排除掉左右两边的点;
- 若 \(A[i+1] < A[i] < A[j]\),则排除掉右边的点;
- 若 \(A[i] < A[j] < A[i+1]\),则排除掉左边的点;
#include
#include
#include
using namespace std;
int main()
{
int n;
scanf("%d", &n);
vector num(n, 0);
for (int i = 0; i < n; i++)
{
scanf("%d", &num[i]);
}
int min_value[n][2];
min_value[1][0] = abs(num[1] - num[0]);
min_value[1][1] = 0;
for (int i = 2; i < n; i++)
{
int j = min_value[i-1][1];
int dis1 = abs(num[i] - num[j]);
int dis2 = abs(num[i] - num[i-1]);
int min_dis = min(dis1, dis2);
int index = dis1 <= dis2 ? j : i-1;
if ((num[i] <= num[j] && num[j] < num[i-1]) || (num[i] < num[i-1] && num[i-1] < num[j]))
{
int left = min(num[i-1], num[j]);
for (int k = 0; k < i - 1; k++)
{
if (num[k] < left)
{
int dis = abs(num[k] - num[i]);
if (dis < min_dis)
{
min_dis = dis;
index = k;
}
else if (dis == min_dis)
{
index = min(index, k);
}
}
}
}
else if ((num[j] <= num[i-1] && num[i-1] < num[i]) || (num[i-1] < num[j] && num[j] < num[i]))
{
int right = max(num[i-1], num[j]);
for (int k = 0; k < i - 1; k++)
{
if (num[k] > right)
{
int dis = abs(num[k] - num[i]);
if (dis < min_dis)
{
min_dis = dis;
index = k;
}
else if (dis == min_dis)
{
index = min(index, k);
}
}
}
}
min_value[i][0] = min_dis;
min_value[i][1] = index;
}
for (int i = 1; i < n; i++)
{
printf("%d %d\n", min_value[i][0], min_value[i][1]+1);
}
return 0;
} 获取更多精彩,请关注「seniusen」!![]()