【数据结构】学习笔记(二)—— 串
文章目录
- 【串】
- I. 串的类型定义
- II. 串的存储表示
- i. 定长顺序存储表示
- ii. 堆分配存储表示
- iii. 块链存储表示
- III. 串的操作实现
- i. 定长顺序存储操作实现
- ii. 堆分配存储操作实现
- iii. 块链存储操作实现
- IV. 串的模式匹配
- i. BF算法
- ii. KMP算法
【串】
I. 串的类型定义
1.串的定义:
串是字符串的简称,其是一种特殊的线性表,其每个元素值仅由一个字符组成。串是由0个或多个字符组成的有限序列,记为S=“a1a2a3…an”。S 是串名,用双引号括起来的部分是串值,n为字符串长度。
由0个字符组成的串称为空串,其长度为0。仅由一个或多个空格组成的串称为空格串,其长度为串中空格字符的个数。
串中任意连续的字符组成的子序列称为子串,原串称为母串。字符在序列中的序号称为该字符在串中的位置,子串在主串中的位置则以子串的第一个字符在主串的第一个字符在主串中的位置来表示。
2.串的抽象数据类型:
ADT String
{
Data:
D={ai|ai∈ElemSet,i=1,2,...,n,n>=0} (具有字符类型的数据元素的集合)
Relation:
R={<a(i-1),ai>|a(i-1),ai∈D,i=2,...,n} (相邻数据元素具有前驱和后继的关系)
Operation:
StrAssign(&S,chars)
初始条件:串常量chars已经存在。
操作结果:将chars赋值给串S。
StrCopy(&T,S)
初始条件:串S已经存在。
操作结果:将S赋值给串T。
DestroyString(&S)
初始条件:串S已经存在。
操作结果:销毁S。
ClearString(&S)
初始条件:串S已经存在。
操作结果:重置为空串。
StrLength(S)
初始条件:串S已经存在。
操作结果:返回串S的元素个数。
StrCompare(S,T)
初始条件:串S和串T已经存在。
操作结果:若S>T,则返回值>0;若S=T,则返回值=0;若S<T,则返回值<0。
StrConcat(&T,S1,S2)
初始条件:串S1和串S2已经存在。
操作结果:返回由S1和S2连接而成的新串T。
SubString\(&Sub,S,pos,len)
初始条件:串S已经存在;1<=pos<=StrLength(S),且0<=len<=StrLength(S)-pos+1。
操作结果:用Sub返回S的第pos个字符起长度为len的子串。
}
ADT String
II. 串的存储表示
i. 定长顺序存储表示
1.定长顺序串:
串中的字符按照其逻辑次序依次存放在这组地址连续的存储单元里的方式称为串的定长顺序存储表示,采用这种存储结构的串称为定长顺序串。
由于定长顺序串的存储空间是在程序执行前分配的,所以其大小在编译的时候就已经确定了。若串的实际长度超过STRING_SIZE,则超过的串值将被截断。所以定长顺序串不适合插入、连接、替换等操作。
2.定长顺序串的长度判断:
1)在串值后面添加一个不计串长的结束标记符,通过判断当前字符是否为‘\0’来确定串是否结束,从而求得串的长度。
2)以下标为0的数组分量存放串的实际长度,串值从下标为1的数组分量开始存放,从而直接得到串的长度。此种方法更为常用。
3.定长顺序串的类型定义:
#define STRING_SIZE 255 //在255内定义最大串长
typedef unsigned char SString[STRING_SIZE+1]; //0号单元存放串的实际长度
ii. 堆分配存储表示
1.堆分配顺序串:
把串中的字符按照其逻辑次序依次存放在这组地址连续的存储单元里的方式称为串的堆分配存储表示,采用这种结构的串称为堆分配顺序串。
堆分配顺序串的存储空间是在程序执行过程中按照串值的实际大小分配的,在进行串操作时不会发生截断,其适用于插入、连接、替换操作。
2.堆分配顺序串的类型定义:
typedef struct
{
char *ch; //存储空间基地址
int length; //串的实际长度
}
HString;
iii. 块链存储表示
1.块链存储结构:
串的块链结构中,每个结点可以存放一个字符,也可以存放多个字符。依据结点大小有两种存储方式:非压缩方式和压缩方式。
为了便于操作,块链存储中还要附设一个尾指针,其指示链表中的最后一个结点,并给出当前串的有效长度。虽然块链存储很适合进行连接操作,但因为其储量大并且操作复杂,其不如定长顺序串和堆分配顺序串灵活。
串的块链存储方式实质上是一种由顺序与链式相结合的复合结构,即块内采用顺序存储结构,块间采用链式存储结构
2.非压缩方式与压缩方式:
非压缩方式的一个结点只存储一个字符,其优点是操作方便,但缺点是存储利用率低。
压缩方式的一个结点可以存储多个字符。对于最后一个结点,如果字符没有占满则补上‘\0’或其他的非串值字符。
3.存储密度:
在块链存储结构中,结点大小的选择会直接影响串处理的效率。串值的存储密度等于串值所占的存储位除以实际分配的存储位的商。
4.块链存储结构的类型定义:
#define Chunk_Size 80 //结点大小
typedef struct Chunk
{
char data[Chunk_Size]; //字符数组
struct Chunk *next; //指向下一块的指针
}
Chunk;
typedef struct
{
Chunk *head,*tail; //串的头指针和尾指针
int length; //串的当前长度
}
LinkString
III. 串的操作实现
i. 定长顺序存储操作实现
赋值操作:
void StrAssign_SS(SString &S,char chars[])
{
i=0;
chars_len=0;
while(chars[i]!='\0') //求chars长度
{
++chars_len;
++i;
}
if(!chars_len) //chars长度为0,生成空串S
{
S[0]=0;
}
else //chars长度非0,生成非空串S
{
j=0;
k=1;
if(chars_len>STRING_SIZE) //复制chars部分字符,发生截断
{
while(k<=STRING_SIZE)
{
S[k++]=chars[j++];
}
S[0]=STRING_SIZE;
cout<<"串常量长度大于给定空间,赋值发生截断!"<<endl;
}
else //复制chars所有字符到S
{
while(k<=chars_len)
{
S[k++]=chars[j++];
}
S[0]=chars_len;
}
}
}
清空操作:
void ClearString_SS(SString &S) //重置定长顺序串S为空串
{
S[0]=0;
}
求串长操作:
int StrLength_SS(SString S) //返回定长顺序串S的长度
{
return S[0];
}
比较操作:
int StrCompare_SS(SString S,SString T) //比较定长顺序串S和T,若S>T则返回值大于0,若S=T则返回值等于0,若S
{
for(i=1;(i<=S[0])&&(i<]T[0]);++i)
{
if(S[i]!=T[i])
{
return (S[i]-T[i]);
}
}
return (S[0]-T[0]);
}
连接操作:
void StrConcat_SS(SString &T,SString S1,SString S2)
{
if((S1[0]+S2[0])<=STRING_SIZE)
{
j=1;
k=1;
while(j<=S1[0])
{
T[k++]=S1[j++];
}
j=1;
while(j<=S2[0])
{
T[k++]=S2[j++];
}
T[0]=S1[0]+S2[0];
cout<<"正确连接,没有发生截断!"<<endl;
}
else if(S1[0]<STRING_SIZE)
{
j=1;
k=1;
while(j<=S1[0])
{
T[k++]=S1[j++];
}
j=1;
while(k<=STRING_SIZE)
{
T[k++]=S2[j++];
}
T[0]=STRING_SIZE;
cout<<"非正确连接,截断串S2,仅取串S1!"<<endl;
}
else
{
j=1;
k=1;
while(j<STRING_SIZE)
{
T[k++]=S1[j++];
}
T[0]=STRING_SIZE;
cout<<"非正确连接。截取串S1!"<<endl;
}
}
求子串操作:
void SubString_SS(SString &Sub,SString S,int pos,int len) //求子串
{
if((pos<1)||(pos>S[0])||(len<0)||(len>(S[0]-pos+1)))
{
cout<<"Position Error!"<<endl;
}
for(i=1;i<=len;i++)
{
Sub[i]=S[pos+i-1];
}
Sub[0]=len;
}
ii. 堆分配存储操作实现
赋值操作:
void StrAssign_HS(String &S,char chars[])
{
i=0;
chars_len=0;
while(chars[i]!='\0')
{
++chars_len;
++i;
}
if(S.ch)
{
delete S.ch;
}
if(!chars_len)
{
S.ch=NULL;
S.length=0;
}
else
{
S.ch=new char[chars_len];
if(!S.ch)
{
Error("Overflow!");
}
j=0;
k=0;
while(k<chars_len)
{
S.ch[k++]=chars[j++];
}
S.length=chars_len;
}
}
销毁操作:
void DestroyString_HS(HString &S)
{
delete [] S.ch;
S.length=0;
}
清空操作:
void ClearString_HS(HString &S)
{
if(S.ch)
{
delete [] S.ch;
S.ch=NULL;
}
S.length=0;
}
求串长操作:
int StrLength_HS(HString S)
{
return S.length;
}
比较操作:
int StrCompare_HS(HString S,HString T)
{
for(i=0;(i<S.length)&&(i<T.length);++i)
{
if(S.ch[i]!=T.ch[i])
{
return (S.ch[i]-T.ch[i]);
}
}
return (S.length-T.length);
}
连接操作:
void StrConcat_HS(HString &T,HString S1,HString S2)
{
if(T.ch)
{
delete T.ch;
}
T.ch=new char[S1.length+S2.length];
if(!T.ch)
{
cout<<"Ovrflow"<<endl;
}
i=0;
k=0;
while(i<S1.length)
{
T.ch[k++]=S1.ch[i++];
}
i=0;
while(i<S2.length)
{
T.ch[k++]=S2.ch[i++];
}
T.length=S1.length+S2.length;
}
求子串操作:
void SubString_HS(HString &Sub,HString S,int pos,int len)
{
if((pos<1)||(pos>S.length)||(len<0)||(len>(S.length-pos+1)))
{
cout<<"Position Error"<<endl;
}
if(Sub.ch)
{
delete Sub.ch;
}
if(!len)
{
Sub.ch=NULL;
Sub.length=0;
}
else
{
Sub.ch=new char[len];
if(!Sub.ch)
{
cout<<"Overflow"<<endl;
}
for(i=0;i<len;i++)
{
Sub.ch[i]=S.ch[pos+i-1];
}
Sub.length=len;
}
}
iii. 块链存储操作实现
void Translation_SS(SString &S,char ch1,char ch2)
{
for(i=1;i<=S[0];i++)
{
if(S.[i]==ch1)
{
S[i]=ch2;
}
}
}
void Invert_SS(SString &S)
{
for(i=1;i<(S[0]/2);i++)
{
t=S[i];
S[i]=S[S[0]-i+1];
S[S[0]-i+1]=t;
}
}
void DeleteChar_SS(SString &S,char ch)
{
for(i=1;i<=(S[0]);i++)
{
if(S[i]==ch)
{
for(j=i;j<(S[0]);j++)
{
S[j]=S[j+1];
}
S[0]=S[0]-1;
}
}
}
void StrReplace_HS(HString &S1,HString &S2,int pos,int len)
{
if((pos<1)||(pos>S1.length)||(len<0)||(len>(S1.length-pos+1)))
{
cout<<"Parameters Error"<<endl;
}
else
{
for(i=0;i<S1.length;i++)
{
a[i]=S1.ch[i];
}
delete [] S1.ch;
S1.ch=new char[S1.length-len+S2.length];
if(!S1.ch)
{
cout<<"Overflow"<<endl;
}
for(i=0;i<pos-1;i++)
{
S1.ch[i]=a[i];
}
for(j=0;j<S2.length;j++)
{
S1.ch[i++]=S2.ch[j];
}
for(k=pos+len-1;k<S1.length;k++)
{
S1.ch[i++]=a[k];
}
S1.length=S1.length-len+S2.length;
}
}
IV. 串的模式匹配
模式匹配即子串的定位操作,即从主串S的第pos个字符开始寻找子串T的过程,如果匹配成功则返回T在S中的位置;若匹配失败,则返回0。
i. BF算法
1.BF算法基本思想:
从主串S第pos个字符开始和模式T第一个字符进行比较,如果相等,则继续比较后续字符;否则从主串S的下一个字符开始和模式T第一个字符进行比较。
2.BF算法设计:
int StrIndex_BF(SString S,SString T,int pos)
{
i=pos; //设置S的起始下标
j=1; //设置T的起始下标
while((i<=S[0])&&(j<=T[0]))
{
if(S[i]==T[j]) //字符相等,继续比较下一字符
{
i++;
j++;
}
else //字符不等,i和j分别回溯
{
i=i-j+2;
j=1;
}
}
if(j>T[0])
{
return (i-T[0]);m //匹配成功,返回T在S中的位置
}
else
{
return 0; //匹配失败,返回0
}
}
3.BF算法分析:
设主串S的长度为n,模式T的长度为m,存在两种极端情况。
在最好的情况下,每趟不成功的匹配都发生在模式T的第一个字符,其时间复杂度为O(n+m);在最坏的情况下,每趟不成功的匹配都发生在模式T的最后一个字符,其时间复杂度为O(n*m)。
ii. KMP算法
1.KMP算法基本思想:
在BF算法的基础上进行改进,主串S不进行回溯,即主串S中的每个字符只参加一次比较。
2.next数组:
next数组的定义如下图所示:
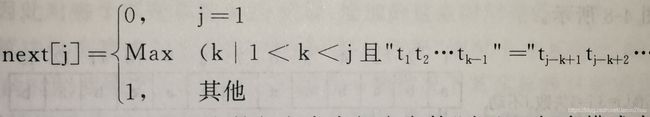
next[j]表明模式中第j个字符与主串中相应字符失配时,在模式中需要重新和主串中该字符进行比较的字符位置。
3.KMP算法设计:
在主串S和模式T中设置比较的下标i和j,循环比较直到S中所剩字符个数小于T的长度或T的所有字符均比较完。如果S[i]=T[j]或j=0,则继续比较S和T的下一个字符;否则将J向右滑动到next[j]的位置,即j=next[j],准备下一趟比较。
如果T中的所有字符均比较完,则匹配成功,否则匹配失败。
int StrIndex_KMP(SString S,SString T,int pos)
{
i=pos; //设置起始下标
j=1;
while((i<=S[0])&&(j<=T[0]))
{
if((j==0)||(S[0]==T[j])) //字符相等或j=0,比较下一个字符
{
i++;
j++;
}
else
{
j=next[j]; //模式T向右移动
}
}
if(j>T[0])
{
return (i-T[0]); //匹配成功
}
else
{
return 0; //匹配失败
}
}
void Get_next(SString T,int &next[]) //利用数组next[]返回模式T的next函数值
{
j=1;
next[1]=0;
k=0;
while(j<T[0])
{
if((k==0)||(T[j]==T[k]))
{
++j;
++k;
next[j]=k;
}
else
{
k=next[k];
}
}
}
4.KMP算法分析:
设主串S长度为n,模式T长度为m,则KMP算法在任何情况下的时间复杂度均为O(m+n)。KMP算法仅在模式与主串存在许多“部分匹配”的情况下才显得比BF算法优越,二者在一般情况下的时间复杂度相当,所以二者均被广泛采用。
KMP算法最大非特点是指示主串的指针不需要再回溯,对主串仅需要从头至尾扫描一编即可匹配,因此对于处理外设输入的庞大的数据文件很有效,其可以边读边匹配,而不需要回头重读。