LCA问题(倍增法)
之前写过了LCA的两个在线算法之一:DFS+ST方法(DFS+ST)。本篇介绍另一种在线算法,用倍增思想来解决LCA问题。在学习倍增之前,先看一种倍增算法的退化版,有助于理解倍增法。
在找a和b的LCA时,先让a和b中深度较大的那一个,向上回溯到与另一个同样深度的位置上。例如下面这个图:
![]()
假设要找F和E的LCA,先让F向上回溯到他的父节点D的位置,这样就与E处在同一深度了。然后让他们同时向上回溯(跳到他们的父节点上),直到两者相遇。相遇时所到达的那个点就是他们的LCA。这种方法很容易理解也很好实现,只需要对树进行一次深度搜索,在搜索过程中将每个点的父节点和他的深度保存下来即可进行上述的查询操作了,结合查询函数代码理解一下:
//fa表示每个点的父节点,deep表示每个点的深度
int fa[100],deep[100];
int LCA(int a,int b)
{
//在函数中确保a的深度大于b的深度,方便后面操作。
if(deep[a]deep[b])
b=deep[b];
//让a和b同时往上跳,直到两者相遇。
while(a!=b)
{
a=deep[a];
b=deep[b];
}
return a;
} 而这种方法最大的问题就是运行太慢了,只能一步一步的往上跳,在很多场景下是不可取的。下面介绍倍增法,这种方法与上面的思路基本一样,但不是一步一步的向前跳,而是巧妙用了倍增的思想和正整数拆分的理论,倍增思想也在ST算法中起了很大作用。先来了解一下倍增法的两个关键理论。
两个关键理论:
- 将2的次幂排成一个序列,即1,2,4,8,16,32......在这个序列中取任意个不相等的数,相加可以得到所有正整数。例如5=1+4;10=2+8;20=4+16,也就是每个正整数都可以拆分成多个2的幂次数。拆分方法也很简单:例如20这个数,先找最接近但不大于20的一个2的幂次数,即16,然后20减去16等于4。再找最接近但不大于4的一个2的幂次数,即4。然后4-4=0,拆分结束,得到了16和4。
- 如果c是a和b的LCA,那么c的所有祖先同样也是a和b的公共祖先,但不是最近的。
- 这两个理论的意义就是:使两个结点不再一层一层地往上跳,而是每次都跳2的幂次方层。例如a点要向上跳10层,就可以跳两次:先跳8层,再跳2层。但是随之而来的新问题是:怎么知道我跳了8层之后到达了哪个结点?下面就要用ST算法来解决这个问题。
倍增法中的ST:
ST算法原本是用来解决区间最大/小值查询的,若不了解ST算法,可以先学习:ST算法。
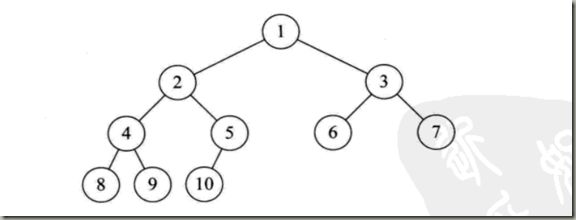
在ST算法中,我们维护了一个数组DP[i][j],表示的是以下标为i为起点的长度为2^j的序列的信息。然后用动态规划的思想求出整个数组。刚才在上面说我们求LCA时一次要跳2的幂次方层,这就与DP数组中下标 j 的定义不谋而合了。所以我们定义倍增法中的DP[i][j]为:结点 i 的向上 2^j 层的祖先。例如下面这个图:
DP[4][1]=1;结点4的向上2^1=2层的祖先是结点1。
DP[10][1]=2;结点10的向上2^1=2层的祖先是结点2。
特别地,DP[6][0]=3,结点6的向上2^0=1层的祖先是3,即6的父节点。而这一现象正好可以当做DP的初始条件。DP[i][0]为i的父节点。下面写出递推式:
DP[i][j] = DP[ DP[i][j-1] ] [j-1]。 如何理解这个递推式呢?DP[i][j-1]是结点i往上跳2^(j-1)层的祖先,那我们就在跳到这个结点的基础上,再向上跳2^(j-1)层,这样就相当于从结点i,先跳2^(j-1)层,再跳2^(j-1)层,最后还是到达了2^j层。这部分的代码如下:
//fa表示每个点的父节点
int fa[100],DP[100][20];
void init()
{
//n为结点数,先初始化DP数组
for(int i=1;i<=n;i++)
dp[i][0]=fa[i];
//动态规划求出整个DP数组
for(int j=1;(1<到这算是完成了整个程序的预处理部分,下面开始写查询函数:
查询函数:
这个函数的参数就是要查询的两个结点a和b。在函数中我们应指定a是深度较大的那个(b也可以),这样方便操作。然后让b不断向上回溯,直到跟a处于同一深度。然后让a和b同时向上回溯,直到二者相遇。这个过程不难理解,但是要实现我们刚才说的一步跳好几层就需要细细思考了。在函数中,共有两次回溯,一次是发生在使a与b处于同一深度时,另一次发生在使a和b共同向上回溯找LCA时,下面我们运用刚才说的两个关键理论对这两次回溯分别进行分析:
- 假设a和b的深度相差5,我们需要让b向上跳,步步逼近a所在的深度,直到与a同深度。如何选取这个步长呢?两个原则:
1、选取的步长肯定不能大于二者的深度差,否则b的深度就小于a的了;
2、选择最接近深度差但又不大于深度差的2的幂次数。这使我们每一步都不会超出a,而且步步逼近a。
那么我们要做的就是本着这两个原则,根据二者的深度差来选取合适的步长,步步逼近。根据正整数拆分理论,不管深度差是多少,二者最后一定能处于同一深度。 - 第二次回溯与第一次不同的是:第一次回溯,已经知道了要跳多少层,所以就可以用正整数拆分理论选择步长。而这次回溯是要找LCA,即找一个层数使a和b跳上去之后正好相遇,也就是说我们只能试探着往上跳,步步逼近。
那我们如何选取a和b同时向上跳的步长?这里用到了我们刚才说的第二个关键理论:若c是a和b的LCA,则c的祖先也是a和b的祖先,但不是最近的。所以这里选取步长的原则就是:大胆地、试探性地往上跳。
可能出现两种情况:
1、若跳到了某一层后a和b相遇了,则说明相遇处的结点就是a和b的公共祖先,但不一定是最近的。这个点就告诉我们:LCA可能还在这个点的下方。那我们就不往这个点上跳,因为这个点有可能不是我们要找的LCA。
2、若跳到了某一层后,a和b没有相遇,则说明a和b的LCA在这层之上,那我们完全可以跳到这一层上,这会使我们步步逼近最终的LCA。根据正整数拆分理论,我们最后也一定能找到LCA。
第一次回溯比较容易理解。重点说一下第二次回溯。换个角度讲,假设我们事先知道LCA与a、b差10层,那么我们如果一步跳了10层以上的话,肯定会跳到LCA的祖先上,那我们就减少步长。如果一步跳8层的话,a和b肯定没有相遇,这时我们就可以跳上来。然后LCA与a、b就差两层了。虽然再跳两层就到了,但是程序只知道这是a和b的公共祖先,但不知道这是不是最近公共祖先,而我们只是开了上帝视角知道了而已,所以程度就会放弃2这个步长,还会将步长减小为1并跳上去。当步长减小为1时,这个试探的过程就可以结束了,因为LCA肯定就是此时a和b的父节点。
不管LCA与a、b差几层,哪怕是8层、4层这种一步就可以跳上去的情况,程序也不会一步跳上去,因为程序总觉得可能这不是最近的公共祖先。而是会步步逼近,直到与LCA只差一层。所以当试探结束后,a和b的父节点就是他们的LCA啦。结合代码理解一下:
//查询函数
int LCA(int a,int b)
{
//确保a的深度大于b,便于后面操作。
if(dep[a]=0;i--)
{
//往上跳就是深度减少的过程
if(dep[a]-(1<=dep[b])
a=dp[a][i];
}
//若二者处于同一深度后,正好相遇,则这个点就是LCA
if(a==b)
return a;
//a和b同时往上跳,从大到小遍历步长,遇到合适的就跳上去,不合适就减少步长
for(int i=19;i>=0;i--)
{
//若二者没相遇则跳上去
if(dp[a][i]!=dp[b][i])
{
a=dp[a][i];
b=dp[b][i];
}
}
//最后a和b跳到了LCA的下一层,LCA就是a和b的父节点
return dp[a][0];
} 至此,倍增法的主要思想和编码就完成了。程序中还剩一小段编码没有完成,就是对树的深搜。在此过程中我们要保存各节点的深度和父节点。保存父节点很简单,求每个结点的深度可以参见我的另一篇:求二叉树各结点的深度。这部分编码没什么太大难度,在这里就不赘述了。
这个算法是我学习过的最美的算法之一,很多思路和细节都值得我们去细细推敲,透彻了思想,编码就不难了。
2019年5月9日更新:
在做一道模板题的时候,发现了倍增更好的写法。洛谷3379
在我上面的陈述中,我是先遍历图,存下所有点的父节点,然后再去一个函数中计算DP数组。但是其实可以在搜图的时候就对每个结点对应DP中的那一行求出来。因为在求DP数组的过程中,我们只关心当前点的某个位置的祖先是什么,也就是说,在当前点之后遍历到的点,对当前点是没有用的。
在我们搜图的过程中,当搜到一个点时,就已经搜过了这个点的所有祖先,只不过我只保存了父节点。所以这时候我们就可以求它在DP数组中的对应行了。我们就不需要fa数组了,而且不需要init函数了。深搜代码如下:
//遍历图,求出各节点的深度,并求出fa数组
int DP[maxn][20],dep[maxn];
void dfs(int root,int pre)
{
dep[root]=dep[pre]+1;
DP[root][0]=pre;
//因为知道了深度,所以我们就可以限定范围了。
for(int i=1;(1<在这道题中,我使用了邻接表来保存图的信息,但是超时了,于是就学习了一种新的数据结构:链式前向星。这个东西可以很好地加快对图的深度或广度搜索。详见:链式前向星