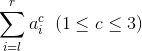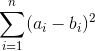SDNU_ACM_ICPC_2020_Winter_Practice_2nd【解题报告】
如果有不懂的地方，那必是我讲得不够清楚，大家可以在评论区中提问或私聊.
对于文章中错误或者不妥的地方，也欢迎大家进行纠错.
目录
A - 【The__Flash】的矩阵
一、题目大意：
二、分析：
三、代码实现：
四、后继：
B - 【The__Flash】的疑惑
一、题目大意：
二、分析：
三、代码实现：
四、后继：
C - 【The__Flash】的电影
一、题目大意：
二、分析：
三、代码实现：
四、后继：
D - 【The__Flash】的排序
一、题目大意：
二、分析：
三、代码实现：
E - 【The__Flash】的操作
一、题目大意：
二、分析：
F - 【The__Flash】的序列
一、题目大意：
二、分析：
三、代码实现：
G - 【The__Flash】的水题
一、题目大意：
二、分析：
三、代码实现：
三、后继：
H - 【The__Flash】的赠予
一、题目大意：
二、分析：
三、代码实现：
I - 【The__Flash】的旅行
一、题目大意：
二、分析：
三、代码实现：
J - 【The__Flash】的球球
一、题目大意：
二、分析：
三、代码实现：
四、后继：
K - 【The__Flash】的牛牛
一、题目大意：
二、分析：
三、代码实现：
L - 【The__Flash】的鲨鲨
一、题目大意：
二、分析：
三、代码实现：
M - 【The__Flash】的达拉崩吧斑得贝迪卜多比鲁翁
一、题目大意：
二、分析：
三、代码实现：
四、后继：
A - 【The__Flash】的矩阵
一、题目大意：
？？？中文题还用我讲ヽ(｀Д´)ﾉ︵ ┻━┻ ┻━┻
二、分析：
之前写过一篇题解，不过太丑了，想看的点我.
考虑一维情况：给出 n 个数 a[1 ~ n]，q 次询问，每次询问给出区间端点 l 和 r，求 ![\sum_{i = l} ^{r} a[i]](http://img.e-com-net.com/image/info8/9ff8ada5a6ba46dc91f80cc72ee2e6e8.gif)
.
对于上述问题，我们可以采用前缀和的方式.
即：预先 O(n) 打出前缀和表 sum[1 ~ n].
当查询 时，可以 O(1) 利用计算公式 sum[r] - sum[l - 1] 求出.
那么此题就是一维的拓展情况，即查询子矩形的和.
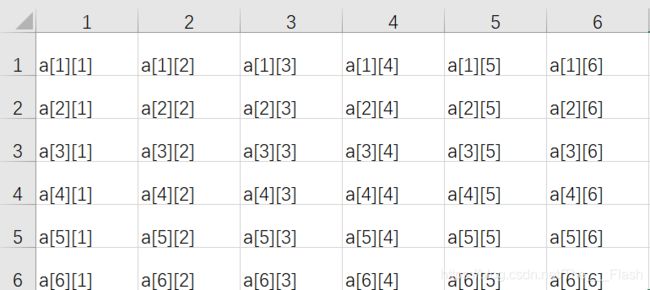
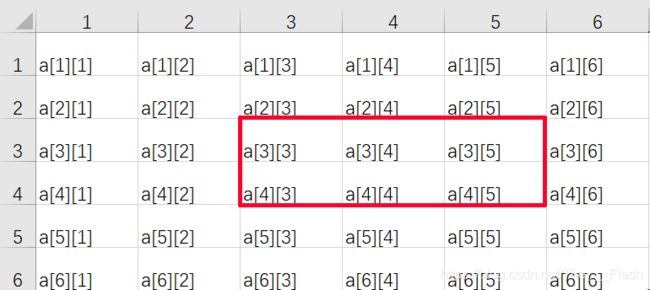
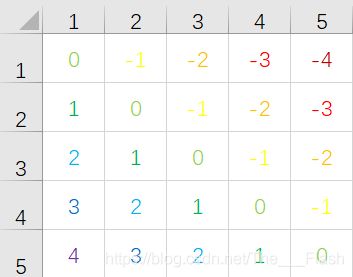
假设现有一矩形如图所示：
那么红色部分的和怎么求呐？
下面直接给出计算公式
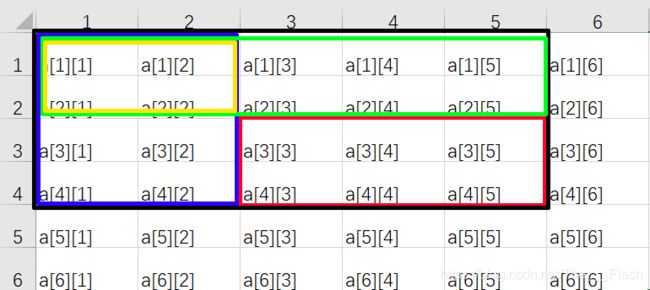
首先进行以下符号化：
红框和为 S
黑框和为 S1
蓝框和为 S2
绿框和为 S3
黄框和为 S4
易得计算公式：S = S1 - S2 - S3 + S4 （基本的容斥思想，也可通过韦恩图来考虑）
由计算公式特点可设 sum[i][j]，表示以 (1, 1) 为左上角 (i, j) 为右下角所构成矩形的和.
因此：
黑框和为 S1 = sum[4][5]
蓝框和为 S2 = sum[4][2]
绿框和为 S3 = sum[2][5]
黄框和为 S4 = sum[2][2]
由此可得：S = sum[4][5] - sum[4][2] - sum[2][5] + sum[2][2]
将公式推广到一般形式：
以 (x1, y1) 为左上角 (x2, y2) 为右下角所构成矩形的和 = sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1].
关于此题，由于矩形的长宽为定值，由此可得：
以 (i, j) 为右下角且长为 x，宽为 y 的矩形的和 = sum[i][j] - sum[i][j - y] - sum[i - x][j] + sum[i - x][j - y].
(不懂的自己画一下图）
Q：师哥，上面的我懂了，不过 sum[i][j] 怎么求呀 ？QAQ
A：不要着急，这就满足你 ♂.
下面以求 sum[4][5] 为例
同样，利用容斥或韦恩图可得：sum[4][5] = sum[4][4] + sum[3][5] - sum[3][4] + a[4][5].
推广到一般形式：
sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + a[i][j].
其中，在求 sum[i][j] 时，上面的量均已求出.
至此大功告成，下面就是愉快的代码时间啦ヾ(✿ﾟ▽ﾟ)ノ
三、代码实现：
#include
using namespace std;
const int M = (int)1e4;
int sum[M + 5][M + 5];
int main()
{
int T;
scanf("%d", &T);
while(T--)
{
int n, m, x, y, data;
scanf("%d %d %d %d", &n, &m, &x, &y);
for(int i = 1; i <= n; ++i)///计算 sum[i][j]
{
for(int j = 1; j <= m; ++j)
{
scanf("%d", &data);
sum[i][j] = sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1] + data;
}
}
int ans = 0;
for(int i = x; i <= n; ++i)///计算以 (i, j) 右下角坐标且大小为 x*y 的矩形的和
{
for(int j = y; j <= m; ++j)
{
ans = max(ans,
sum[i][j] - sum[i][j - y] - sum[i - x][j] + sum[i - x][j - y]);
}
}
printf("%d\n", ans);
}
return 0;
}
四、后继：
1. 值得一提的是，这道题数组下标从 1 开始的解法相较于从 0 开始是更简单的，仔细想想为什么？
2. 学有余力的同学，可以看看这道题.
3. 2.中的这道题是否可以继续优化呢？（提示：线段树）
B - 【The__Flash】的疑惑
一、题目大意：
Q：有人没看懂题吗？
A：都看懂啦，题目简洁易懂
就是不会做(逃...
二、分析：
B 题是双权值最短路，只需在最短路的基础上修改更新语句.
PS：最短路试炼场
三、代码实现：
#include
using namespace std;
const int M = (int)1e3;
const int N = (int)1e5;
const int inf = 0x3f3f3f3f;
int cnt;
int head[M + 5];
struct node
{
int v, d, p, nx;
}Edge[N * 2 + 5];///双向边
bool vis[M + 5];
int d[M + 5];
int p[M + 5];
void init(int n)
{
cnt = 0;
for(int i = 1; i <= n; ++i)
{
head[i] = -1;
vis[i] = 0;
d[i] = inf;
p[i] = inf;
}
}
void add(int u, int v, int d, int p)
{
Edge[cnt].v = v;
Edge[cnt].d = d;
Edge[cnt].p = p;
Edge[cnt].nx = head[u];
head[u] = cnt++;
}
struct cmp
{
bool operator()(int a, int b)
{
if(d[a] != d[b])
return d[a] > d[b];
return p[a] > p[b];
}
};
priority_queue , cmp> q;
void spfa(int s)
{
q.push(s);
vis[s] = 1;
d[s] = 0;
p[s] = 0;
while(!q.empty())
{
int u = q.top();
q.pop();
vis[u] = 0;
for(int i = head[u]; ~i; i = Edge[i].nx)
{
int v = Edge[i].v;
if(d[v] > d[u] + Edge[i].d)///距离最短
{
d[v] = d[u] + Edge[i].d;///同时更新 d 与 p
p[v] = p[u] + Edge[i].p;
if(!vis[v])
{
q.push(v);
vis[v] = 1;
}
}
else if(d[v] == d[u] + Edge[i].d &&
p[v] > p[u] + Edge[i].p)///距离相同时，花费最小
{
p[v] = p[u] + Edge[i].p;
if(!vis[v])
{
q.push(v);
vis[v] = 1;
}
}
}
}
}
int main()
{
int n, m;
int a, b, d, p;
while(~scanf("%d %d", &n, &m) && (n + m))
{
init(n);
while((m--) > 0)
{
scanf("%d %d %d %d", &a, &b, &d, &p);
add(a, b, d, p);
add(b, a, d, p);
}
int s, t;
scanf("%d %d", &s, &t);
spfa(s);
printf("%d %d\n", ::d[t], ::p[t]);
///"::变量"作用：由于存在局部和全局同名变量，此用法可访问全局变量（其实就是懒得起变量名）
}
return 0;
}
四、后继：
1. 存边时要注意是单向边还是双向边，如果是双向边要开 2 倍的数组空间.
2. 要计算长度的最大值，即 （点数 - 1）* 边权最大值，由此来选择是 int 还是 long long
其中，int 范围的 inf = 0x3f3f3f3f（4 个 3f）; long long 范围的 inf = 0x3f3f3f3f3f3f3f3f （8 个 3f）
C - 【The__Flash】的电影
一、题目大意：
有 n 个人，每个人会且仅会一种语言.
有 m 个电影，电影语言分为 音频语言 和 字幕语言，且同场电影的音频语言和字幕语言不同.
当人观看电影时，如果他会该电影的音频语言，他会非常高兴.
当人观看电影时，如果他会该电影的字幕语言，他会比较高兴.
现要求选择一场电影，使得非常高兴的人数最多，若解不唯一，则选择比较高兴人数最多，输出该电影的编号.
二、分析：
Q：这题真简单，直接用 num[i] 表示会第 i 种语言的人数
然后更新最大值即可.
就像这个样子. （疯狂炫耀ing）
scanf("%d", &n); for(int i = 1; i <= n; ++i) scanf("%d", &a[i]); scanf("%d", &m); for(int i = 1; i <= m; ++i) scanf("%d", &b[i]); for(int i = 1; i <= m; ++i) scanf("%d", &c[i]); for(int i = 1; i <= n; ++i) num[a[i]]++; int ans = 1; int num1, num2; int num1_max, num2_max; num1_max = num2_max = 0; for(int i = 1; i <= m; ++i) { num1 = num[b[i]]; num2 = num[c[i]]; if(num1 > num1_max || num1 == num1_max && num2 > num2_max) { num1_max = num1; num2_max = num2; ans = i; } } printf("%d\n", ans);可是一编译发现不妙，数组太大啦.
师哥师哥，这可咋办呀っﾟДﾟ)っ
A：hhh，虽说 a, b, c 的数据范围太大，数组开不下.
但是 n 的范围还是可以接受哒.
由于 a, b, c 具体的值并不重要，只需要维持原有的大小关系
例如：20 20 520 可以 重新编号为 1 1 2，这对答案的求解是无影响的
基于这种思想，我们可以对 a, b, c 进行重新编号，这样最多只有 3e5 个不同的数，就可以很轻松的解决啦.
Q：师哥tql，不过该怎么样重新编号呢？
A：我们通常将重新编号叫做【离散化】
那么离散化的步骤就是：
1. 将数据写到一个数组 d 中
2. 将数组 d 进行排序（sort()）
3. 排序后对数组 d 进行去重（unique()）
当询问元素的相对大小时，由于数据有序，我们可以采用二分查找的方式查询元素 x 的位置.
三、代码实现：
#include
using namespace std;
const int M = (int)2e5;
int a[M + 5];
int b[M + 5];
int c[M + 5];
int d[M * 3 + 5];
int n, m, len;
int num[M + 5];
void discrete()///离散化
{
len = 0;
for(int i = 1; i <= n; ++i) d[++len] = a[i];
for(int i = 1; i <= m; ++i) d[++len] = b[i];
for(int i = 1; i <= m; ++i) d[++len] = c[i];
sort(d + 1, d + len + 1);
len = unique(d + 1, d + len + 1) - (d + 1);
}
int tofind(int x)///二分查找元素 x 在 d 中的位置
{
return lower_bound(d + 1, d + len + 1, x) - d;
}
int main()
{
scanf("%d", &n);
for(int i = 1; i <= n; ++i) scanf("%d", &a[i]);
scanf("%d", &m);
for(int i = 1; i <= m; ++i) scanf("%d", &b[i]);
for(int i = 1; i <= m; ++i) scanf("%d", &c[i]);
discrete();
for(int i = 1; i <= n; ++i) num[tofind(a[i])]++;
int ans = 1;
int num1, num2;
int num1_max, num2_max;
num1_max = num2_max = 0;
for(int i = 1; i <= m; ++i)
{
num1 = num[tofind(b[i])];
num2 = num[tofind(c[i])];
if(num1 > num1_max ||
num1 == num1_max && num2 > num2_max)
{
num1_max = num1;
num2_max = num2;
ans = i;
}
}
printf("%d\n", ans);
return 0;
}
四、后继：
思考：上述代码中，为什么要把 a, b, c 都加入 d 中呢，如果只加入 a 会怎样？
D - 【The__Flash】的排序
一、题目大意：
有 n 个任务，每次只能做一个.
给出 m 个关系，每个关系有两个数字 a 和 b，表示作业 a 必须在 作业 b 之前完成.
求作业的完成顺序是怎样的，若答案不唯一，则输出任意一组即可.
二、分析：
见群内 PPT by Albert_s
三、代码实现：
#include
using namespace std;
const int M = (int)1e2;
int cnt;
int head[M + 5];
struct node
{
int v, nx;
}Edge[M * M + 5];
int in[M + 5];///入度
void init(int n)
{
cnt = 0;
for(int i = 1; i <= n; ++i)
{
head[i] = -1;
in[i] = 0;
}
}
void add(int u, int v)
{
Edge[cnt].v = v;
Edge[cnt].nx = head[u];
head[u] = cnt++;
}
queue topoq;///记录拓扑序
void toposort(int n)
{
queue q;
for(int i = 1; i <= n; ++i)
{
if(!in[i])
{
topoq.push(i);
q.push(i);
}
}
while(!q.empty())
{
int u = q.front();
q.pop();
for(int i = head[u]; ~i; i = Edge[i].nx)
{
int v = Edge[i].v;
if(!--in[v])
{
q.push(v);
topoq.push(v);
}
}
}
}
int main()
{
int n, m;
while(~scanf("%d %d", &n, &m) && (n + m))
{
init(n);
int u, v;
while((m--) > 0)
{
scanf("%d %d", &u, &v);
add(u, v);
in[v]++;
}
toposort(n);
bool flag = 0;
while(!topoq.empty())
{
if(flag)
printf(" ");
printf("%d", topoq.front());
topoq.pop();
flag = 1;
}
printf("\n");
}
return 0;
}
E - 【The__Flash】的操作
一、题目大意：
有 n 个数，初始化为 0.
有 4 种操作：
1 l r c：区间 [l, r] 中的数 + c
2 l r c：区间 [l, r] 中的数 * c
3 l r c：区间 [l, r] 中的数 = c
4 l r c：输出 
二、分析：
很明显的懒惰标记线段树，不过这里有三种操作，比较难搞.
需要逐个分析标记和更新的顺序，之前写过一篇题解（丑...），就挂在这啦 ヾ(✿ﾟ▽ﾟ)ノ
Q：师哥你好懒啊...
A：口住！
貌似有更简单的解法，tql，orzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzzz
F - 【The__Flash】的序列
一、题目大意：
n 个数，要求选择其一子序列（不要求连续），使得子序列的和为奇数且最大.
二、分析：
水题.
先把所有正数加起来，如果 sum 为奇数，则输出 sum.
如果 sum 为偶数，那么就去掉最小的正奇数 或者 加上最小的负奇数，两个答案取最大值.
（这题没做出来的是不是该好好反思一下...）
三、代码实现：
#include
using namespace std;
const int M = (int)1e5;
const int inf = 0x3f3f3f3f;
int a[M + 5];
int main()
{
int n;
scanf("%d", &n);
for(int i = 1; i <= n; ++i)
scanf("%d", &a[i]);
int sum = 0;
for(int i = 1; i <= n; ++i)
{
if(a[i] > 0)
sum += a[i];
}
if(sum & 1)
printf("%d\n", sum);
else
{
sort(a + 1, a + n + 1);
int ans = -inf;
for(int i = 1; i <= n; ++i)
{
if(a[i] > 0 && a[i] & 1)
{
ans = max(ans, sum - a[i]);
break;
}
}
for(int i = n; i >= 1; --i)
{
if(a[i] < 0 && a[i] & 1)
{
ans = max(ans, sum + a[i]);
break;
}
}
printf("%d\n", ans);
}
return 0;
}
G - 【The__Flash】的水题
一、题目大意：
两个长度相同的字符串 s 和 t.
现有如下操作：
s[i - 1] = s[i] 或 s[i + 1] = s[i] 或 t[i - 1] = t[i] 或 t[i + 1] = t[i].
问对 s 或 t 进行任意次此操作后，s 与 t 是否能相等.
二、分析：
题目都叫做水题了...
只需要判断 s 和 t 中是否有相同的字符.
三、代码实现：
#include
using namespace std;
const int M = (int)1e2;
char s[M + 5], t[M + 5];
void work()
{
int len = strlen(s + 1);
for(int i = 1; i <= len; ++i)
{
for(int j = 1; j <= len; ++j)
{
if(s[i] == t[j])
{
printf("YES\n");
return;
}
}
}
printf("NO\n");
}
int main()
{
int T;
scanf("%d", &T);
while(T--)
{
scanf("%s %s", s + 1, t + 1);
work();
}
return 0;
}
三、后继：
思考：如果 s 和 t 的长度最大为 1e6，该怎样做呢？
H - 【The__Flash】的赠予
一、题目大意：
大小为 n 的两个序列 A, B.
现序列 A 进行 k1 次操作，每次操作使得序列 A 中的一个数 + 1 或 - 1.
现序列 B 进行 k2 次操作，每次操作使得序列 B 中的一个数 + 1 或 - 1.
求 
的最小值.
二、分析：
简单贪心.
首先，易得题目条件等价于对序列 A 进行 k1 + k2 次操作，每次操作使得序列 A 中的一个数 + 1 或 - 1.
显然，每次选择将 abs(a[i] - b[i]) 取最大值的 a 进行操作.
其中，若 a[i] > b[i]，则 a[i]--;
否则， a[i]++;
由于数据范围过小，这里直接用优先队列暴力求解.
不会自定义优先队列排序的同学看这里呀！
值得注意的是，最终答案会爆 int，需要用 long long 存储.
三、代码实现：
#include
using namespace std;
typedef long long ll;
const int M = (int)1e3;
struct node
{
int a, b;
}s[M + 5], tmp;
struct cmp
{
bool operator()(node x, node y)
{
return abs(x.a - x.b) < abs(y.a - y.b);
}
};
priority_queue , cmp> q;
int main()
{
int n, k1, k2;
scanf("%d %d %d", &n, &k1, &k2);
for(int i = 1; i <= n; ++i) scanf("%d", &s[i].a);
for(int i = 1; i <= n; ++i) scanf("%d", &s[i].b);
for(int i = 1; i <= n; ++i) q.push(s[i]);
for(int i = 1; i <= k1 + k2; ++i)
{
tmp = q.top();
q.pop();
if(tmp.a > tmp.b)
tmp.a--;
else
tmp.a++;
q.push(tmp);
}
ll ans = 0;
while(!q.empty())
{
tmp = q.top();
q.pop();
ans += 1ll * (tmp.a - tmp.b) * (tmp.a - tmp.b);
}
printf("%lld\n", ans);
return 0;
}
I - 【The__Flash】的旅行
一、题目大意：
有一个 n 个点的无向完全图，现有 m 条边的权值为 a，剩下边的权值为 b.
求 1 ~ n 的最短路.
二、分析：
显然直接暴力是跑不动的.
从只有两种权值的路下手
考虑，若 1 和 n 之间有权值为 a 的边直接相连，那么就只有两种选择：
1. 直接走 1 到 n 的路，花费为 a.
2. 只走边权为 b 的路 （因为如果 a、b 混合着走，显然不如第一种方案优）
同理，若 1 和 n 之间无权值为 a 的边直接相连，那么就只有两种选择：
1. 直接走 1 到 n 的路，花费为 b.
2. 只走边权为 a 的路 （因为如果 b、a 混合着走，显然不如第一种方案优）
那么现在问题就变成了 只走边权为 b 的路所需最小花费 和 只走边权为 a 的路所需最小花费.
对于后者，由于边权为 a 的路的数量最多只有 5e5，所以直接 spfa 或 dijkstra 即可.
对于前者，边权为 b 的路的数量级最多是 1e10，下面直接给出做法（补图最短路）.
由于只走边权为 b 的路，所以每条路的权值相同，此时可用 bfs（因为 bfs 的搜索顺序：按层搜索），先搜到的点最短路则确定.
用两个集合 s1， s2
其中，s1 表示未访问过且从当前点可到达的点，s2 表示未访问过且从当前点无法到达的点.
那么每次从队列中选择队首元素，即可从 s1 集合中开始拓展，对于没有边相连的点，说明当前点可到达.
嘤嘤嘤，直接看代码吧 ｡◕ᴗ◕｡
三、代码实现：
#include
using namespace std;
typedef long long ll;
const int M = (int)1e5;
const int inf = 0x3f3f3f3f;
int cnt;
int head[M + 5];
struct node
{
int v, nx;
}Edge[M * 10 + 5];
int dis[M + 5];
bool vis[M + 5];
bool flag;
void init(int n)
{
cnt = flag = 0;
for(int i = 1; i <= n; ++i)
{
vis[i] = 0;
dis[i] = inf;
head[i] = -1;
}
}
void add(int u, int v)
{
Edge[cnt].v = v;
Edge[cnt].nx = head[u];
head[u] = cnt++;
}
int bfs(int n, int s, int t)
{
queue q;
set s1, s2;
set :: iterator iter;
q.push(s);
dis[s] = 0;
for(int i = 1; i <= n; ++i)
{
if(i != s)
s1.emplace(i);
}
while(!q.empty())
{
int u = q.front();
q.pop();
for(int i = head[u]; ~i; i = Edge[i].nx)
{
int v = Edge[i].v;
if(!s1.count(v)) continue;
s1.erase(v), s2.emplace(v);
}
for(iter = s1.begin(); iter != s1.end(); ++iter)
{
dis[*iter] = dis[u] + 1;
q.push(*iter);
}
s1.swap(s2), s2.clear();
/**
s1.swap(s2) 只交换首指针，是 O(1) 操作
swap(s1, s2) 交换集合内所有元素，是 O(n) 操作
**/
}
return dis[t];
}
struct cmp
{
bool operator()(int a, int b)
{
return dis[a] > dis[b];
}
};
priority_queue , cmp> q;
int spfa(int n, int s, int t)
{
q.push(s);
vis[s] = 1, dis[s] = 0;
while(!q.empty())
{
int u = q.top();
q.pop();
vis[u] = 0;
for(int i = head[u]; ~i; i = Edge[i].nx)
{
int v = Edge[i].v;
if(dis[v] > dis[u] + 1)
{
dis[v] = dis[u] + 1;
if(!vis[v])
{
q.push(v);
vis[v] = 1;
}
}
}
}
return dis[t];
}
ll work(int n, int a, int b)
{
if(flag)
return min(1ll * a, 1ll * bfs(n, 1, n) * b);
else
return min(1ll * b, 1ll * spfa(n, 1, n) * a);
}
int main()
{
int n, m, a, b;
while(~scanf("%d %d %d %d", &n, &m, &a, &b))
{
init(n);
for(int i = 0, u, v; i < m; ++i)
{
scanf("%d %d", &u, &v);
if(u == 1 && v == n || u == n && v == 1)
flag = 1;
add(u, v);
add(v, u);
}
printf("%lld\n", work(n, a, b));
}
return 0;
}
J - 【The__Flash】的球球
一、题目大意：
长度为 n 的区间，每次操作给出子区间的端点 a，b，代表给区间 [a, b] 进行覆盖，最后输出每个点被覆盖的次数.
二、分析：
简答差分.
Q：师哥，差分是是啥呀？_(:з」∠)_
A：差分就是前缀和的逆过程.
举例来讲，高中学习的数列
和
的关系.
即：
取 l + 1 = r 且 符号化为 i，则
即：
是由相邻两项
的差表示
此时，我们将
易得：
（下面用得到）
Q：师哥讲得真棒，可是差分有什么用呢？
A：那让我们来看一下这道题吧.
每次都要覆盖一次区间，若采用暴力做法时间复杂度将达到
现采用差分的思想对其进行优化.
将覆盖次数看做
，设其差分序列为
（初始值为 0）
显然：
当进行区间 [a, b] 覆盖时，我们可以进行如下操作.
p[a]++, p[b + 1]--;
分析此操作后
可见，此操作使得区间 [a, b] 之间的数都 + 1，其余的数保持不变，且修改一次是
的.
Q：师哥我好笨，还是没听懂...
A： 宁也太菜了，快来看视频讲解！
三、代码实现：
#include
using namespace std;
const int M = (int)1e5;
int p[M + 5];
int main()
{
int n;
while(~scanf("%d", &n) && n)
{
for(int i = 1; i <= n; ++i)
p[i] = 0;
int l, r;
for(int i = 1; i <= n; ++i)
{
scanf("%d %d", &l, &r);
p[l]++;
p[r + 1]--;
}
int cnt = 0;
for(int i = 1; i <= n; ++i)
{
cnt += p[i];
printf("%d%c", cnt, i == n ? '\n' : ' ');
}
}
return 0;
}
四、后继：
1. 相似题目
2. A 题是二维前缀和，那有没有二维差分呐？
K - 【The__Flash】的牛牛
一、题目大意：
给定一个正整数数列，求一个平均数最大的，长度不小于 f 的子串，输出平均值 * 1000取整后的结果.
二、分析：
这这这...二分就好了嘛
实数域上二分平均值，check(mid) 检查是否存在长度不小于 f 且平均值不小于 mid 的子串.
这里有一个小技巧：把每个数都减去 mid，则问题转化为了 检查是否存在长度不小于 f 且和不小于 0 的子串. （巨佬请忽略）
记 b[i] = a[i] - mid, sum[i] = b[1] + b[2] + ... + b[i]
则只需找到一个区间 [l, r]，使得 sum[r] - sum[l -1] > 0.
那我们只需记录 sum[l - 1] 最小值即可在 O(n) 时间复杂度内完成.
三、代码实现：
#include
#include
using namespace std;
const int M = (int)1e5;
const double eps = 1e-5;
const int inf = 0x3f3f3f3f;
int n, f;
int a[M + 5];
double b[M + 5];
double sum[M + 5];
bool check(double mid)
{
for(int i = 1; i <= n; ++i)
b[i] = a[i] - mid;
for(int i = 1; i <= n; ++i)
sum[i] = sum[i - 1] + b[i];
double Min = inf * 1.0;
for(int i = f; i <= n; ++i)
{
Min = min(Min, sum[i - f]);
if(sum[i] - Min > 0)
return 1;
}
return 0;
}
int main()
{
scanf("%d %d", &n, &f);
for(int i = 1; i <= n; ++i)
scanf("%d", &a[i]);
double l = 0, r = 2000, mid;
while(r - l > eps)
{
mid = (l + r) / 2.0;
if(check(mid))
l = mid;
else
r = mid;
}
printf("%d\n", (int)(r * 1000));
return 0;
}
L - 【The__Flash】的鲨鲨
一、题目大意：
给出 n 个点的坐标，求有多少个 点对 在同一对角线上.
二、分析：
两个点在同一对角线上说明 x + y 或 x - y 相等.
例如：
x + y：
x - y：
因此可以用 a[i] 存 x + y == i 点的个数，b[i] 存 x - y == i 的点的个数.
由于 x - y 可为负，因此可用 b[i + M] 存 x - y + M == i 的点的个数.
三、代码实现：
#include
using namespace std;
typedef long long ll;
const int M = (int)1e3;
int a[M * 2 + 5];
int b[M * 2 + 5];
int main()
{
int n;
scanf("%d", &n);
int x, y;
for(int i = 1; i <= n; ++i)
{
scanf("%d %d", &x, &y);
a[x + y]++;
b[x - y + M]++;
}
ll ans = 0;
for(int i = 1; i <= M * 2; ++i)
{
ans += 1ll * a[i] * (a[i] - 1) / 2;
ans += 1ll * b[i] * (b[i] - 1) / 2;
}
printf("%lld\n", ans);
return 0;
}
M - 【The__Flash】的达拉崩吧斑得贝迪卜多比鲁翁
一、题目大意：
很久很久以前
巨龙突然出现
带来灾难带走了公主又消失不见
王国十分危险
世间谁最勇敢
一位勇者赶来大声喊
“我要带上最好的剑
翻过最高的山
闯进最深的森林
把公主带回到面前”
国王非常高兴忙问他的姓名
年轻人想了想
他说
“陛下我叫达拉崩吧斑得贝迪卜多比鲁翁
再来一次
达拉崩巴斑得贝迪卜多比鲁翁”
“是不是达拉崩吧斑得贝迪卜多比鲁翁”
“对对达拉崩巴斑得贝迪卜多比鲁翁”
...
幽幽小路上，英雄达拉崩吧遇到 n 只怪兽
每只怪兽有其相应的体力值 HP 和 攻击值 ATK
达拉崩吧每次可对怪物造成一次伤害，伤害值为 K（其中，K 在数值上为达拉崩吧攻击这只怪兽的次数）
然鹅，每次存活的怪兽都可以攻击我们的英雄达拉崩吧
当怪兽的体力值小于等于时，怪兽死亡.
现请你选择一种打怪兽的顺序，使得达拉崩吧收到的伤害和最小，并输出收到最小的伤害和.
二、分析：
贪心.
首先明确一件事情：“打一只怪兽一次没打死，再去打另一只怪兽” 显然不是最优解.
即：打怪兽时一定是打这只怪兽到死亡，再去打另一只怪兽.
那么问题就转化成了安排打怪兽的顺序，使得收到的伤害和最小.
这里采用临项交换法求解.
设 f(HP)：打体力值为 HP 的怪兽所需次数
假设现在有两只怪兽 a 和 b，体力值分别为 HP[a], HP[B]，攻击值分别为 ATK[a], ATK[b].
若先打怪兽 a，再打怪兽 b，那么伤害值为：
![f(HP[a]) \times ATK[a] + (f(HP[a]) + f(HP[b])) \times ATK[b].](http://img.e-com-net.com/image/info8/758bc61e2e26468b9e30c1d2db631b40.gif){kind=small}
若先打怪兽 b，再打怪兽 a，那么伤害值为：
![f(HP[b]) \times ATK[b] + (f(HP[b]) + f(HP[a])) \times ATK[a].](http://img.e-com-net.com/image/info8/396e80a501754a1c8e165a5c69d4ab35.gif){kind=small}
假设第一种方案为最优解，则
![f(HP[a]) \times ATK[a] + (f(HP[a]) + f(HP[b])) \times ATK[b] \\ < \ f(HP[b]) \times ATK[b] + (f(HP[b]) + f(HP[a])) \times ATK[a].](http://img.e-com-net.com/image/info8/b9e7198750a3445b8a5f90ef66484a67.gif){kind=small}
化简可得：
![f(HP[a]) \times ATK[b] < f(HP[b]) \times ATK[a].](http://img.e-com-net.com/image/info8/f9aec48b9fed4461a865c346665e7e9f.gif){kind=small}
也可化为：
![\frac{f(HP[a])}{ATK[a]} < \frac{f(HP[b])}{ATK[b]}](http://img.e-com-net.com/image/info8/81c7a93d2f4e40f48dc8300d57c9c6d4.gif){kind=small}
综上可得：只需要按照上式进行排序，得到的序列即为打怪兽的最优顺序.
Q：师哥，那 f(HP) 怎么求呢 [・_・?]
A：由攻击规则可知：
第 i 次攻击伤害为 i
设需要攻击这只怪兽 n 次
可得：
由于
在 n > 0 单调递增，因此可用二分求解 n.
三、代码实现：
#include
using namespace std;
typedef long long ll;
const int M = (int)1e5;
struct node
{
int ATK, HP;
}s[M + 5];
int f(int HP)
{
int l = 1, r = 500, mid;
while(l < r)
{
mid = (l + r) >> 1;
if(mid * (mid + 1) / 2 >= HP)
r = mid;
else
l = mid + 1;
}
return r;
}
bool cmp(node a, node b)
{
return f(a.HP) * b.ATK < f(b.HP) * a.ATK;
}
int main()
{
int T;
scanf("%d", &T);
for(int ca = 1; ca <= T; ++ca)
{
int n;
scanf("%d", &n);
for(int i = 1; i <= n; ++i)
scanf("%d %d", &s[i].HP, &s[i].ATK);
sort(s + 1, s + n + 1, cmp);
ll ans = 0, cnt = 0;
for(int i = 1; i <= n; ++i)
{
cnt += f(s[i].HP);
ans += cnt * s[i].ATK;
}
printf("Case #%d: %lld\n", ca, ans);
}
return 0;
}
四、后继：
常见贪心证明手段：
1. 临项交换：
证明在任何局面下，任何对局部最优策略的微小改变都会造成整体结果变差，经常用于以“排序”为贪心策略的证明.
2. 范围缩放：
证明任何对局面最优策略作用范围的拓展都不会造成整体结果变差.
3. 决策包容性：
证明在任意局面下，作出局部最优决策以后，在问题状态空间中的可达集合包含了作出其他任何决策后的可达集合。换言之，这个局部最优策略提供的可能性包含其他所有策略提供的可能性.
4. 反证法
5. 数学归纳法
例题：
POJ-3614
POJ-3190
POJ - 1328
国王游戏
POJ-2054