山东科技大学2015-2016学年第一学期程序设计基础期末考试第一场 题解
山东科技大学2015-2016学年第一学期程序设计基础期末考试第一场 题解
A题 花坛
Description
学校要修一些圆形的花坛,每个花坛外围铺一圈大理石的地面。现在知道花坛的内圆半径r米和大理石地面的外圆半径R米,求大理石地面的面积。

圆周率取3.14159。
Input
输入两个浮点数r和R。
Output
输出大理石地面的面积,精确到小数点后三位。
Sample Input
2 3
Sample Output
15.708
标程
#include这道题思想很简单,就是将大圆和小圆的面积求出,二者相减即可,唯一需要注意的就是保留三位小数采用.3lf即可
B题 夏季促销
Description
商场夏季促销,购物399元(含)以上,95折;购物899元(含)以上,9折;购物2499元(含)以上,85折;购物4899元(含)以上,8折。并且不收取角分部分。
根据购物金额,确定用户实际需要支付的数目。
Input
输入客户购买若干物品的单价金额,均为正整数,至EOF结束。
Output
输出用户实际需要支出的数目,以元为单位,保留两位小数。
Sample Input
105
398
742
82
888
276
Sample Output
2241.00
标程
#include这道题有一处小细节,就是最后打折后不收取角分的部分,也就是说计算出结果后,数值向下取整,那么最后的.00直接进行输出就行了
C题 鸡兔同笼
Description
鸡兔同笼是中国古代的数学名题之一。大约在1500年前,《孙子算经》中就记载了这个有趣的问题。书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”
一个笼子里关了鸡和兔子(鸡有2只脚,兔子有4只脚,没有例外)。已知鸡和兔的总头数为n,总腿数为m。输入n和m,依次输出鸡的数目和兔的数目。如果无解,则输出“no result”。
Input
首先输入一个正整数k<20,表示有k组测试数据。
每组测试输入正整数n和m(均小于1000),分别表示鸡兔的总头数及总腿数。
Output
每行依次输出鸡的数目和兔的数目,用一个空格分开。如果无解,则输出“no result”。
Sample Input
2
35 94
10 42
Sample Output
23 12
no result
标程
#include假设笼子中鸡的数量为x,兔的数量为y
可以列出如下方程:
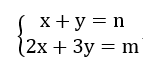
通过解方程可以得到如下公式
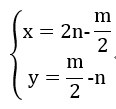
通过解出的公式可以知道m必须为奇数,并且x,y均不小于0,通过这几个条件的特判就可以得出答案
D题 递归求和
Description
输入一组数字,用递归的方法求和。
Invalid Word(禁用单词)错误:在解决这个题目时,某些关键词是不允许被使用的。如果提交的程序中包含了下列的关键词之一,就会产生这个错误。
被禁用的关键字:循环语句for、while,甚至包括分支语句的switch、case、goto。
Input
第一行输入一个正整数k(k<1000),第二行为k个整数。
Output
输出这k个整数的和。
Sample Input
10
1 2 3 4 5 6 7 8 9 10
Sample Output
55
标程
#include通过题目描述可以知道,这道题即使输入数据都要使用递归的方式,也就是说函数的主体是一个递归函数,现在可以想一下递归的最底层就是当n=1的情况,这时候读入最后一个数字,返回数值,之后逐步将读入的数值加到和里面返回即可
E题 哥德巴赫猜想的证明
Description
验证“每个不小于6的偶数都是两个奇素数之和”,输入一个不小于6的偶数n,找出两个奇素数,使它们的和为n。
Input
输入一个不小于6的偶数n,n<10000。
Output
找出两个奇素数,使它们的和为n。如果有多种答案,则每个答案占一行。注意:在输出时,第一个数不能大于第二个数。比如对于10,输出的答案只有3 + 7 = 10,没有7 + 3 =10。
每行的输出格式为:
a + b = c
a和b是满足条件的两个数,a<=b,c为输入的数。
多个答案的输出顺序,要按照第一个数递增的顺序输出。
Sample Input
20
Sample Output
3 + 17 = 20
7 + 13 = 20
HINT
注意:1是素数吗?
标程
#include这道题就是将输入的数字进行拆分,拆分的结果必须满足如下几个条件:
1.两个数必须为素数
2.前一个数必须严格不大于第二个数
3.输出时,按第一个数递增输出
按照如下条件就能很简单的写出程序
F题 登录密码验证 之二
Description
编写一个程序,模拟用户登录系统的密码验证过程。系统提供给用户的密码长度最长为20个字符,若密码输入错误可以再次输入。但为了保证用户密码安全,若连续输入密码错误超过5次就会锁定账号一段时间。
与此前不同的是,这次系统的密码验证是大小写无关的,也就是说同一个英文字母的大、小写视作相同字符。
Input
输入为若干个串,至EOF结束。输入的第一个串是用户的正确密码,后面的串为模拟用户登录时的输入的密码。
Output
每次输入错误的密码,输出一个“Wrong!”,若输入的密码为正确的,输出一个“Welcome!”,并结束密码测试。若前5次输入的密码都是错误的,则后面的输入中不管是否有正确的密码都输出“Out of limited!”。
Sample Input
ABCDEFG
123456 kkkkkkkk abcdefg
Sample Output
Wrong!
Wrong!
Welcome!
标程
#include这道题相比之前的登陆密码判断一那道题唯一的区别就是密码不区分大小写,这样的话,就需要对输入的字符串进行预处理,可以全部预处理为大写或者全部预处理为小写,预处理后再逐步进行比较,需要注意的是一但密码匹配则程序退出,不管之后是否还有数据输入,当输入次数大于5次的时候,不管密码是否正确全部输出Out of limited!注意到这几点之后就可以很容易写出程序。
G题 数字的千位分隔
Description
把整数利用逗号进行千位分隔并输出。
Input
输入第一行是整数T(0
对应每一行数据输入,输出一行用逗号进行千位分隔的数字串。
Sample Input
3
12
123
12345
Sample Output
12
123
12,345
标程
#include所谓的千位分隔就是说要让数字从后向前每三位输出一个分隔符,这样从前往后逐步判断是否符合即可,需要对数字的第一位和最后一位进行特判即可
H题 用结构体来表示数组
Description
有如下结构体定义:
typedef struct
{
int length;
int array[MAX_SIZE];
}ARR_TYPE;
其中,length表示数组中实际元素的个数,array[]用于存储length个数据,MAX_SIZE表示数组的最大长度。
要求编写如下两个函数
- int input_arr(ARR_TYPE *arr);
用于按照样例给定的格式输入arr的内容。 - int output_arr(ARR_TYPE arr);
用于按照样例给定的格式输出arr中array的内容。
注意:提交时要提交相关的预处理命令(#include、#define等)以及结构体类型定义。
Input
输入只有一行,第一个数N表示后面会有N个整数,其中0
输出只有一行,按照输入的顺序输出所有整数,两两之间用空格隔开。
Sample Input
10 1 2 3 4 5 6 7 8 9 10
Sample Output
1 2 3 4 5 6 7 8 9 10
int main()
{
ARR_TYPE arr;
input_arr(&arr);
output_arr(arr);
return 0;
}
标程
#include一个结构体的简单应用,运用函数,将数据读入后输出即可
I题 求众数
Description
一组数据中出现次数最多的数值,叫众数,有时众数在一组数中有好几个。
Input
有多组测试数据。输入的第一行是整数T(0
对应每组测试数据,输出出现最多的数的出现次数,同时输出出现最多的数,如果有多个数
出现次数都是最多,按从小到大顺序输出。
Sample Input
1
10 1 2 3 2 1 2 3 1 1 3
Sample Output
4 1
标程
#include这道求众数的题目思想很简单,有数据描述可以知道,输入的数据个数不超过1000个,并且包整输入的数据大小不超过10000,由此我们可以定义一个大小为10000的数组,用来记录相同的数字的个数,最后所有数据输入结束后,扫一遍数组,统计出现次数最多的数字的次数,之后在进行一次循环,输出出现次数为最大次数的数字,即可,按题目要求的格式输出数据即可
J题 杨辉三角
题目描述
杨辉三角,又称贾宪三角形,帕斯卡三角形,是二项式系数在三角形中的一种几何排列。在欧洲,这个表叫做帕斯卡三角形。帕斯卡(1623----1662)是在1654年发现这一规律的,比杨辉要迟393年,比贾宪迟600年。
下图的表在我国南宋数学家杨辉1261年所著的《详解九章算法》一书里就出现了。其中下一层的每一项都是由上一层连边的两项相加得来。
输入
输入多组,每组一个正整数n<14,至EOF结束。
输出
每组输入对应输出n层的杨辉三角,每一项占4个字符,除了每行开始需要填充空格之外,任意两项之间不要有多余的空格。
两组输出之间用一个空行分开,最后一组数据之后不要添加空行。
输出详细格式见sample。
样例输入
7
5
样例输出
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
标程
#include这里运用的是杨辉三角的一个性质num[i][j]=num[i-1][j]+num[i-1][j-1],既然已知n的值不超过14,那么可以按性质将杨辉三角的前14行全部产生出来,之后按照格式输出,需要注意的是每个数字占四个字符,并且每一行要输出空格
K题 一共多少天
Description
安琪的18岁生日就要到了,她当然很开心。她想到了一个问题,是不是每个人从出生开始,到达18岁生日时所经过的天数都是一样的呢?似乎并不都是一样的。于是,她想编写一个程序来计算她和她的几个朋友从出生到达18岁生日所经过的总天数是多少?
Input
一个数T(T<=100),后面T行每行有一个日期,格式是YYYY-MM-DD。如安琪的生日是1988-03-07。日期均为正数,且合法。
Output
T行,每行一个数,表示此人从出生到18岁生日所经过的天数。如果这个人没有18岁生日,就输出-1。
Sample Input
1
1988-03-07
Sample Output
6574
标程
#include这里有一个提示,就是可能会有人过不了18岁生日(笑哭),当一个人的生日为2月29日时,这个人每四年过一次生日,这样这个人时没有18岁生日的,需要输出-1,这是一个特殊的地方,需要特判,其次一旦出现每年的天数问题,首先就是2份,如果这个人的生日是在2月及2月之前,那么这个人的的过生日的天数由本年决定,如果这个人的生日在2月之后不包括2月,则这个人的生日由次年决定,主要是由2月份所在的年份来决定,其次就是闰年的判断,闰年是可以被4整除但不能被100整除或者可以被400整除的数。
