【暖*墟】#三分法# 求单峰函数极值
【三分法】
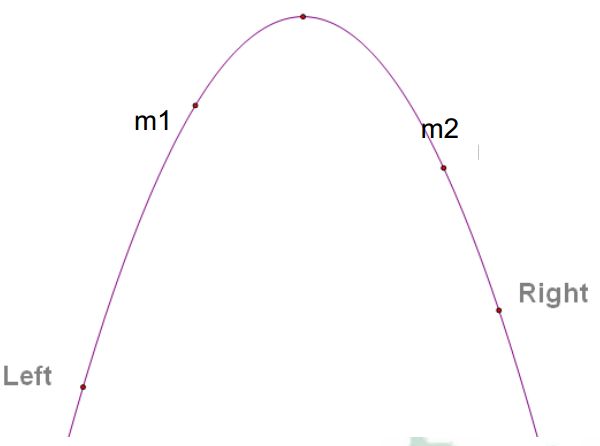
1. 对于任意一个上凸函数,选取函数上任意两个点A,B(xA
若满足yA
若满足yA>yB,那么该函数极值点必然在(-∞,xB]中,
若满足yA=yB,那么该函数的极值点必然在[xA,xB]中。
2. 对于任意一个下凸函数,选取函数上任意两个点A,B(xA
若满足yA
若满足yA>yB,那么该函数极值点必然在[xA,+∞)中,
若满足yA=yB,那么该函数的极值点必然在[xA,xB]中。
三分法的思路与二分法很类似,不过其用途没有那么广泛,主要用于求单峰函数的极值。
此处,任选的点为m1,m2。与l,r把区间分成三段。
void Solve(){
double left, right, m1, m2, m1_value, m2_value;
left = MIN;
right = MAX;
while (left + EPS < right){
m1 = left + (right - left)/3;
m2 = right - (right - left)/3;
m1_value = f(m1);
m2_value = f(m2);
if (m1_value >= m2_value)
right = m2; //假设求解极大值
else left = m1;
}
}BZOJ1857 传送带 (三分法求单峰函数极值)
1.题目描述
在一个2维平面上有两条传送带,每一条传送带可以看成是一条线段。两条传送带分别为线段AB和线段CD。lxhgww在AB上的移动速度为P,在CD上的移动速度为Q,在平面上的移动速度R。现在lxhgww想从A点走到D点,他想知道最少需要走多长时间?
2.题目分析
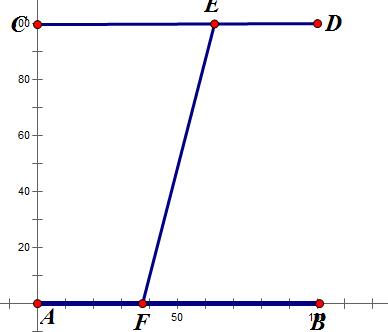
把样例画出来,如下图:
答案必然是从AB上的某一个点出发,经过平面,到达CD上的另一点然后到达D。
即答案可以表示为:
|AF|/P+|FE|/R+|ED|/Q ,其中F∈AB,E∈CD
我们考虑将F点(你喜欢E点就E点)确定,那么剩下的问题就在于确定E点
(若前面选择E点那就是确定F点,以后就统一E点算了)。
那么怎么确定E点呢,生活常识告诉我们,在CD上肯定有一个最优的解,
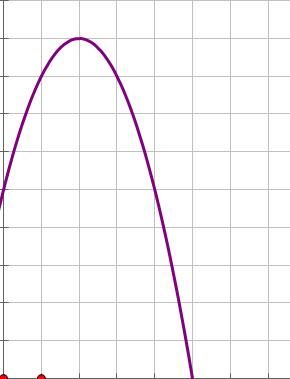
这个点两侧的解都越来越差,即函数图像大致为下面这样:
容易看出这是一个单峰函数,还是一个上凸的单峰函数,
那么我们的问题就暂时变为了求这个单峰函数的极值。
用了三分法后,我们得到了解决了对于某个特定点F,如何求得最优的E点的方法,
但是,问题中并没有给出F点在哪,那该怎么办?
这时,我们可以思考这样一个问题:如果我们已知某个确定的点E,
能够用三分法求出F吗,显然我们可以,那么我们就可以考虑用三分法的方法确定一个F,
然后再通过这个F确定另一个E,即三分套三分。
【例题2】
#include
#include
using namespace std;
const double EPSINON = 0.000001;
int a,b,c,x,y;
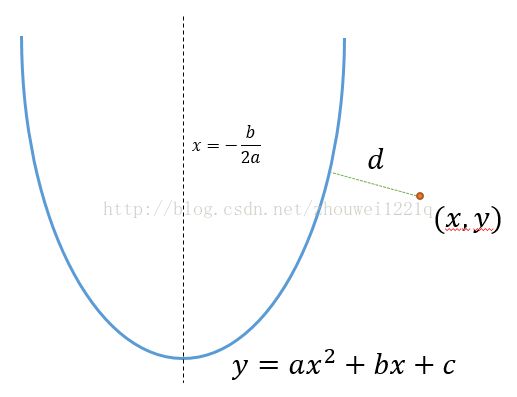
double Distance(double tempx)
{
return sqrt(pow(tempx-x, 2) + pow(a*tempx*tempx+b*tempx+c-y, 2));
}
double Calculate(double left, double right, double dist_left, double dist_right)
{
double temp = (right-left)/3.0; //把区间等分为三块
double temp_left = left+temp;
double temp_right = right-temp;
double ldist = Distance(temp_left);
double rdist = Distance(temp_right);
if(fabs(left-right) < EPSINON ){ //终止条件
return (dist_left+dist_right)/2;
}
else{
if(ldist < rdist){ //左区间的距离小的话,就在左边找
return Calculate(left, temp_right, dist_left, rdist);
}
else if(ldist > rdist){ //右区间的距离小的话,就在右边找
return Calculate(temp_left, right, ldist, dist_right);
}
else{ //左右相等,则在中间找
return Calculate(temp_left, temp_right, ldist, rdist);
}
}
}
int main()
{
cin>>a>>b>>c>>x>>y;
double result = 0;
double mid;
double width = 500.0;
mid = static_cast(-b)/(2*a);
if(x > mid){
result = Calculate(mid,mid+width, Distance(mid), Distance(mid+width));
}
else if(x < mid){
result = Calculate(mid-width, mid, Distance(mid-width), Distance(mid));
}
else{ //当点在对称轴上时,取点到抛物线顶点的距离和根据算法算出来的距离的最小值
result = min(Distance(x), Calculate(mid, mid+width, Distance(mid), Distance(mid+width)));
}
printf("%.3lf", result);
system("pause");
return 0;
} //非递归方法:
#include