739、503、496、1019、84、85 给定一个数组，求每个元素右/左边第一个比它大/小的元素

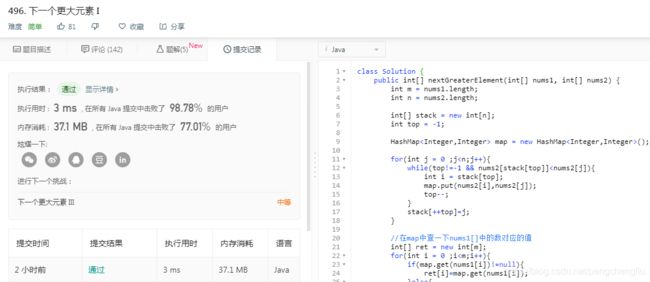
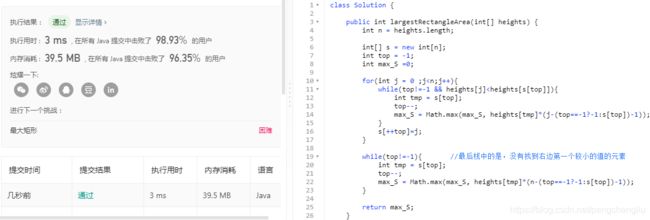
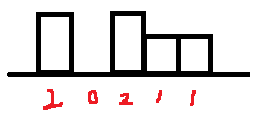
例题：739  给定一个数组，求每个元素右边第一个比它大的元素  Medium                                        点击此处返回总目录            扩展1：给定一个数组，求每个元素右边第一个比它小的元素            扩展2：给定一个数组，求每个元素左边第一个比它小的元素            扩展3：给定一个数组，求每个元素左边第一个比它大的元素 习题1、503  循环数组中，求每个元素右边第一个比它大的元素  Medium 习题2、496  给定一个数组，求某些元素右边第一个比它大的元素 Easy 习题3、1019  给定一个链表，求每个元素右边第一个比它大的元素 Medium 习题4、84    柱状图中的最大矩形  Hard 习题5、85    给定一个矩阵，找出全为1的面积最大的矩阵 Hard   ------------------------------------------------------------------------------------------------------------------------------- 例题：739  给定一个数组，求每个元素右边第一个比它大的元素  Medium   【题目】   【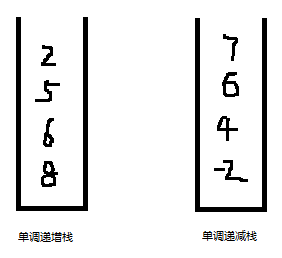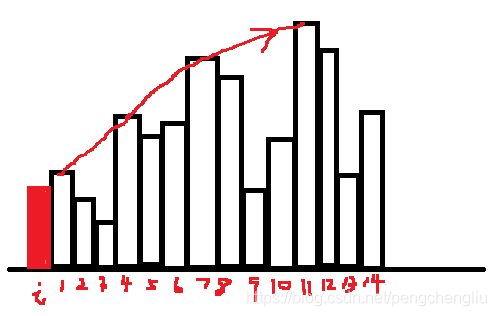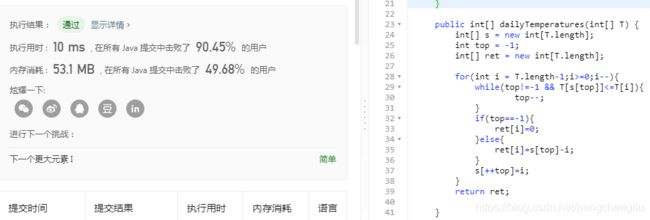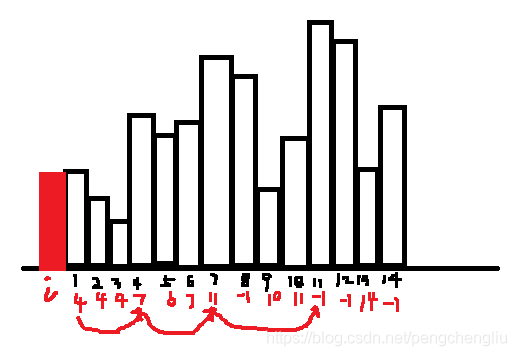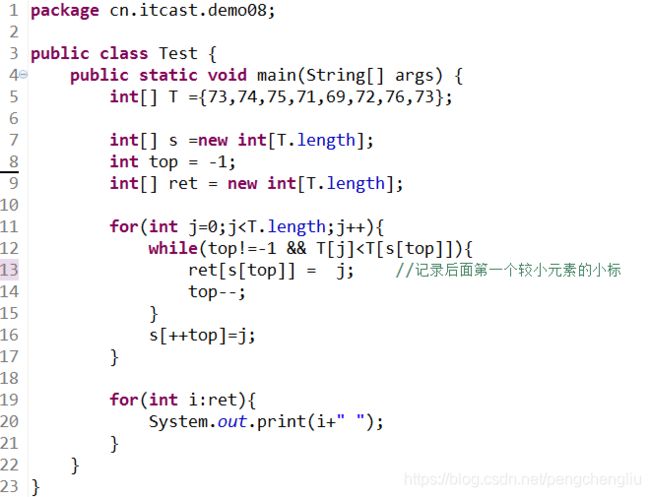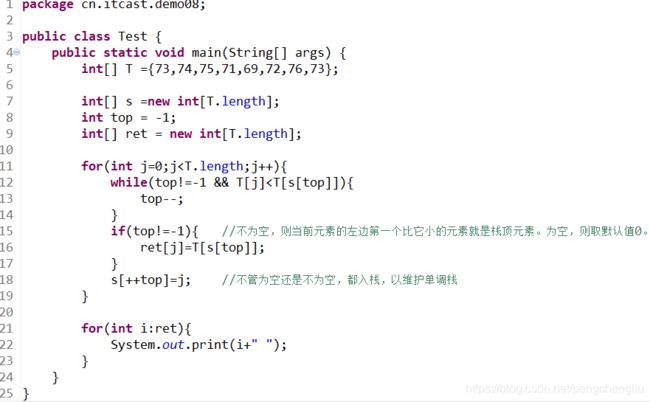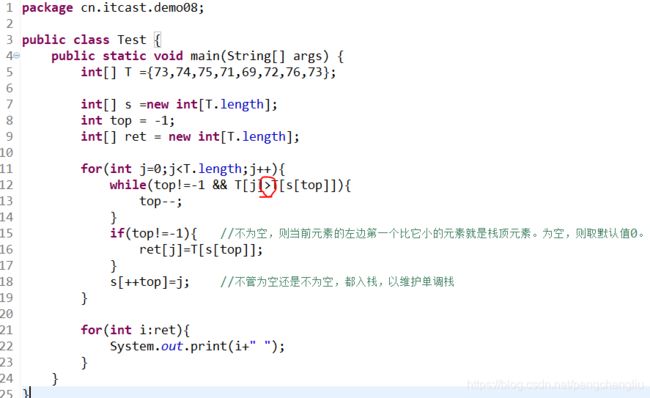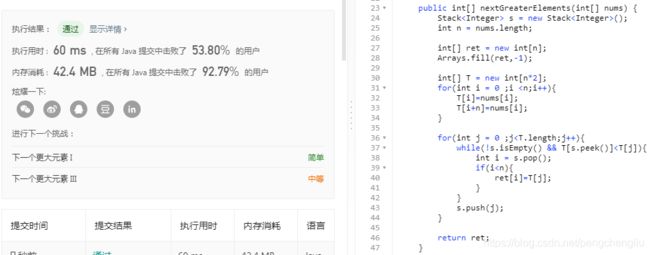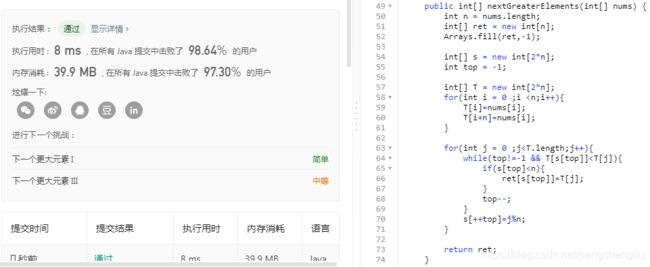分析】 首先想到的是两重循环。 for(int i = 0 ;i     for(int j = i+1 ;j < len ;j++){         if(T[j]>T[i]){             ....         }     } } 但是时间复杂度为o(n^2)，肯定超时。这道题没那么简单。     【方法一：单调栈】 单调栈的概念： 我们用一个栈来解决。单调栈，其实就是一个普通的栈而已，只不过里面的元素是单调的而已。 单调栈分为单调递增栈和单调递减栈。查了很多资料发现是这样定义的：                                                    跟我想的是相反的。居然顺序是按照从栈顶到栈底看的。不知道定义的人是怎么想的啊。 我以后就把单调递增栈叫做：“栈顶元素小的单调栈”，把单调递减栈叫做：“栈顶元素大的单调栈”了。   题目分析： 上面是基础知识，我们看一下这个例子怎么用单调栈来做。                                   比如当前要求比i大的第一个元素。i后面有14个元素。此时： 如果i小于第1个元素，那结果显然就是第1个元素。 如果i大于第1个元素，那就再跟第4个元素比较，即跟第1个元素右边比第一个元素大的元素比较。而第2第3个元素不需要比，因为都比第一个元素大了，肯定比第2,3个元素大。如果小于第4个元素，结果就是第4个元素；否则就跟第7个元素比，不需要跟5,6比。 所以i只需要跟1,4,7,11这几个元素比较即可。   所以，只要记录下当前元素的后一个元素开始的一个递增序列（注意，这不是任意的一个递增序列）即可。怎么做呢？我们用一个单调栈来做。   维护一个初试为空的栈。从后往前遍历数组T：     代码：   结果：   效果一般般。   改进：通过数组代替栈。 定义栈：            int[] s = new int[T.length];            top = -1;                                  //栈顶。   则一般栈的功能为：            查看栈顶元素：      s[top]            入栈：                    s[++top] =a;            出栈：                    top--;             为空：                    top == -1   代码：     结果：       【方法二：同样的思想用递推实现】   还是上面的想法： 如果i小于第1个元素，那结果显然就是第1个元素。 如果i大于第1个元素，那就再跟第4个元素比较，即跟第1个元素右边比第一个元素大的元素比较。而第2第3个元素不需要比，因为都比第一个元素大了，肯定比第2,3个元素大。如果小于第4个元素，结果就是第4个元素；否则就跟第7个元素比，不需要跟5,6比。 所以i只需要跟1,4,7,11这几个元素比较即可。   刚才的方法是用一个栈来维护这个递增序列。但是大可不必这么做，因为我们倒着求的时候，ret[]数组记录下了右边第一个比当前元素大的元素的下标。我们可以利用这个结果。     代码：   结果：       【方法三：另一种单调栈】 这种方法也很巧妙。可以这么记："一步一回头，见到小的就收"。 思想是这样的，栈中保存的是当前还没有找到下一个较大值的那些点。比如1，2，3号。当来了一个4号时，就可以得到123号的值了。                                     伪代码如下： 顺序遍历T，对于每一个元素T[i]：        当然最后的判断语句可以去掉。   代码：   结果：   改进： 我们同样使用数组来代替栈。   替换后的代码：     结果：   【总结】 本题我们给了以下几种方法： 暴力法                 //忘记吧 从后往前的单调栈及数组代替 从后往前的递推 从前往后的单调栈及数组代替   要求最后一种方法能够深刻理解掌握默写。   只要掌握了这个题目，下面的几道题目就可以迎刃而解。   ------------------------------------------------------------------------------------------------------------------------------- 扩展一：给定一个数组，求每个元素右边第一个比它小的元素   刚才的思想是：见到小的就收。现在是反过来，见到大的就收。 如果当前元素比栈中的元素大，就压栈。如果当前元素比栈中的元素小，就出栈，并且栈中元素的下一个较小元素就是当前元素。                               很容易写出代码：             只比上一个代码该了一个符号。   执行结果：     扩展二：给定一个数组，求每个元素左边第一个比它小的元素                               我们看刚才的"求右边第一个比它小的元素"，维护了一个栈顶大的单调栈。 比如当前的元素是第4个元素，栈中的元素是第1,2,3个元素。第4个比第3个小，所以第3的左边第一个比它小的元素是第4个。第4个比第2个要小，所以第2个的右边第一个比它小的元素是第4个。然后4进栈。                                            我们从另一个角度来看：当第4个元素要进栈的时候，此时栈顶的元素就是4左边第一个比4小的元素，也就是1。因为比4大的2和3已经出来了。剩下的栈顶元素就是比它小的。   所以，跟求元素左边第一个比它小的元素 也是维护一个栈顶元素大的单调栈。     代码：   结果：     扩展三：给定一个数组，求每个元素左边第一个比它大的元素 同理，维护一个栈顶小的单调栈。当元素入栈的时候，栈顶元素就是当前元素左边第一个较小的元素。         只比上一个代码改了一个符号。   结果：     总结： 1. 求右边第一个比它大的元素、求左边第一个比它大的元素   都是用  栈顶元素小的单调栈。【739】、【扩展三】     求右边第一个比它小的元素、求左边第一个比它小的元素   都是用  栈顶元素大的单调栈。【扩展一】、【扩展二】     2. 维护一个栈顶小的单调栈。当新来一个元素i时，如果i比栈顶大，则出栈且出栈元素的右边第一个比它大的元素就是i；如果i比栈顶小，则入栈且i的左边第一个比i大的元素就是栈顶元素。     维护一个栈顶大的单调栈。当新来一个元素i时，如果i比栈顶小，则出栈且出栈元素的右边第一个比它小的元素就是i；如果i比栈顶大，则入栈且i的左边第一个比i小的元素就是栈顶元素。     3. 核心代码总结如下：   4.    可以同时求出元素右边第一个比它大的元素和元素左边第一个比它大的元素。因为都是维护同一个栈。当出栈时，可以求出右边第一个大的元素，当进栈时，可以求出左边第一个比它大的元素。    可以同时求出元素右边第一个比它小的元素和元素左边第一个比它小的元素。因为都是维护同一个栈。当出栈时，可以求出右边第一个小的元素，当进栈时，可以求出左边第一个比它小的元素。       ------------------------------------------------------------------------------------------------------------------------------- 习题1、503  循环数组中，求每个元素右边第一个比它大的元素  Medium   【题目】   【分析】 最先想到双重循环。 代码： 结果肯定是很慢。     我们想其他的办法。循环数组，常用的技巧就是把数组写两遍。然后问题就转换为了上一个题：求元素后面第一个比它大的元素。 比如：1 8 7 2 4 6 。想要的结果为：8 -1 8 4 6 8 。 写两遍就是：  1   8   7   2   4   6   1   8   7   2   4   6 其结果为：      8  -1  8   4   6   8   8   7   0   4   6   -1   我们可以看到：前面n个的结果是我们想要的，后面一半的结果是我们不想要的。 因此，我们只需要求出前n个即可。   上面的方法中，从后往前的单调栈（及数组实现）、递推不好用。使用从前往后的单调栈（及数组实现）比较方便，即上题的方法三。     【方法：从前往后的单调栈】   代码如下：   有几个地方需要注意一下： 1. 第28行，首先把ret都设置成-1。因为元素下标是0~n-1，出现0代表下一个较大的元素是0，而没有找到下一个数则应该为-1。在上题中默认值是0。这一题如果出现0，在最后的时候，需要将栈的数据清空，然后设置成-1。（因为栈中存放的是，找不到下一个较大值的点。所以找不到较大值的点最后还待在栈中没有出栈）。这样就比较麻烦，还不如一上来设置初值为-1。 2. ret[]的大小是n。所以在39行的地方加个判断，当出栈的元素下标     结果：     【改进】 同样，我们使用数组代替栈：     结果：       -------------------------------------------------------------------------------------------------------------------- 习题2、496  给定一个数组，求某些元素右边第一个比它大的元素 Easy   【题目】   【分析】 这个题跟第一题没什么区别啊。 首先求第二个数组中每个元素的后一个较大的数字。然后使用HashMap<>存放一下<数字，右边比它大的第一个数>。 最后再查找一下nums1中想要看哪些值就行了。     【代码】     【结果】     ----------------------------------------------------------------------------------------------------------------------------   习题3、1019  给定一个链表，求每个元素右边第一个比它大的元素 Medium   【题目】   【分析】 一看这道题就是第一题的变形。不同的是第一题是数组，这个题是链表。 首先，链表是从前往后遍历的。因此，我们只能使用从前往后的单调栈这种方法。而从后往前的单调栈、从后往前的递推不能用，除非先倒置链表。   确定了使用从前往后的单调栈之后就好想了。我们第一题用一个栈来存下标，然后根据下标得到数组对应元素。但是链表中根据下标得到对应元素，需要遍历。因此，我门可以搞两个同步栈。一个存放下标，另一个存放对应的元素。   【代码】   【结果】     --------------------------------------------------------------------------------------------------------------------------   习题4、84  柱状图中的最大矩形 Hard   【题目】     【分析】 要求勾勒出的最大矩形。可以分别求出包含每个柱子的最大矩形，然后求最大。 比如，包含第n个柱子的最大矩形为：               怎么求包含第i个柱子的面积是多少呢？ 高就是第i个柱子的高度。宽度就是从"该柱子左边第一个比它小的柱子"到"该柱子右边第一个比它大的柱子"的距离（不包含首尾）。比如，柱子5的左边第一个比5小的柱子是1，右边第一个比5小的元素是2，那么包含柱子5的最大矩阵的宽度是2（2的下标-1的下标-1）。   因此问题转化为了，求当前元素左右两边第一个比它小的元素。使用单调栈即可。   我们前面讲了求元素左边第一个比它小的元素和求元素右边第一个比它小的元素，都是用的同一个单调栈。只不过，求右边第一个小的元素时，是出栈时确定。左边第一个小的元素是进栈时决定。因此，可以将代码合并，同时求出两边第一个小的元素。     【代码】   【结果】     【另一个版本】   刚才是求出来最后求最大面积，也可以在出栈的时候，就求最大面积。因为出栈的时候，就知道右边较小数的下标了。出栈之后栈顶的元素就是左边较小数。因此，在看别人的代码时，也经常有下面这个版本。大同小异。   代码： 也可以首先在数组后面增加元素0。这样就可以省下最后一个while，因为所有元素都能找到右边第一个较小值，就不会最后栈还不为空。     结果：     要求记住第二个版本的写法。能够理解着记忆。     ------------------------------------------------------------------------------------------------------------------------------- 习题5、85    给定一个01矩阵，找出全为1的面积最大的子矩阵 Hard     【题目】   【分析】 这道题确实很难。既然放在这里，肯定是使用单调栈来解决。但是即使提醒是单调栈，也一般想不出来。 我们直接说思路。我们使用了84题的方法。   （1）我们把前1行的数字当做柱子，为：                            这样就可以使用84题的方法，求出所有底边在第1行的矩形中，面积最大的矩形。最大面积为1。   （2）把前两行的数字当做柱子，为：                             使用84的方法，就可以求出所有底边在第2行的矩形中，面积最大的矩形。最大面积为3。   （3）把前3行的数字当做柱子，为：                            使用84题的方法，就可以求出，底边在第3行的所有矩形中，面积最大的矩形。最大面积为6。   （4）把前4行的数字当做柱子，为：                             使用84题的方法，就可以求出，底边在第4行的所有矩形中，面积最大的矩形。最大面积为4。   （5）求完之后就确定了，最终结果为6。     【代码】     内部的for循环，跟84题完全一样~~   【结果】