leetcode 42. Trapping Rain Water最大水域 收集雨水

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

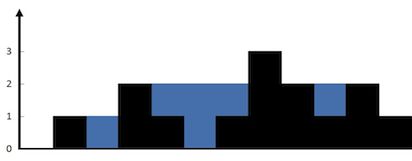
The above elevation map is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped. Thanks Marcos for contributing this image!

Example:

Input: [0,1,0,2,1,0,1,3,2,1,2,1]
Output: 6

解法一：
收集雨水：只需要记录当前位置左侧最大值，右侧最大值，如果当前位置高度小于左侧最大值和右侧最大值的最小值，则当前位置的积水量为 这个最小值 减去 当前位置高度，否则当前位置不积水。
用vector 容器记录当前位置的最大值和最小值。
所以空间复杂度为o(2n),时间复杂度为o（3n）。
代码如下：

int trap(vector& height) {
        int res=0,mx=INT_MIN,n=height.size();
        vector  maxleft(n,INT_MIN);// 一个大小为n容器，初始化为最小值，记录左侧最大值
        vector  maxright(n,INT_MIN);// 一个大小为n容器，初始化为最小值，记录右侧最大值
        for(int i=0;i=0;--i){
            maxright[i]=mx;
            mx=max(mx,height[i]);
        }
        for(int i=1;i

解法二：
对解法一进行优化 空间复杂度o（n），时间复杂度o（2n），用一个容器。

    int trap(vector& height) {
        int res=0,mx=INT_MIN,n=height.size();
        vector  maxdp(n,INT_MIN);// 一个大小为n容器，初始化为最小值，记录当前位置的左侧最大值和右侧最大值的较小者

        for(int i=0;i=0;--i){
            maxdp[i]=min(mx,maxdp[i]);//记录当前位置的左侧最大值和右侧最大值的较小者
            mx=max(mx,height[i]);
            if(height[i]

解法三：
时间复杂度为O（1），空间复杂度为O（n）

    int trap(vector& height) {
        int res=0,l=0,r=height.size()-1,lever=INT_MIN;
        while(l

更好理解了

    int trap(vector& height) {
        int res=0,l=0,r=height.size()-1,leftmax=INT_MIN,rightmax=INT_MIN;
        while(l=leftmax)leftmax=height[l];
                else res+=leftmax-height[l];
                ++l;//递增
            }
            else{//左边值大于右边值，不需要知道左面最大值，只需要知道右面最大值
                if(height[r]>=rightmax)rightmax=height[r];
                else res+=rightmax-height[r];
                --r;//递减
            }
        }
        return res; 

还可以用堆栈方法解决。