最优化-线性规划-单纯形法1

单纯形法 simplex

基本上这是个耳熟能详求解线性规划的算法，大学运筹课学的也还给了老师。只能再花时间学习下，线性规划的格式也很通俗，如下：
$$\begin{array}{r}subject:\min /\max \left(z\right)=cx\\ Constraints:Ax=b\\ A_{1}x\le b_1\\ A_{2}x\ge b_2\\ x\in \mathbb{R}\\ b,b_1,b_2\in \mathbb{R}\end{array}$$
以上格式包含所有情况。但是为了进行计算，一般需要将格式转化成标准格式，如下：
$$\begin{array}{r}subject:\min /\max \left(z\right)=cx\\ Constraints:Ax=b\\ x\ge 0\\ b\ge 0\end{array}$$
转化逻辑为反转、添加松弛变量、剩余变量等。将目标转化成最小或者最大均可，为方便代码实现，建议转换成统一的格式，不然需要加入if、else来判断增加计算量和代码量。
转化对象有目标函数、决策变量、约束条件中的关系和右项值。
1.对于目标函数而言，若是求最大则无需转换，若是求最小 则需要在两端各乘以-1。
2.对于决策变量，若本身大于等于0，则无需转化，若是小于等于0，需将目标函数和该决策变量所代表的系数乘以-1。若为实数，需添加两个新的变量。
3.对于右项值，若大于等于0，则无需转化，若小于0，则需要在两端各乘以-1.
截取清华大学运筹学第三版

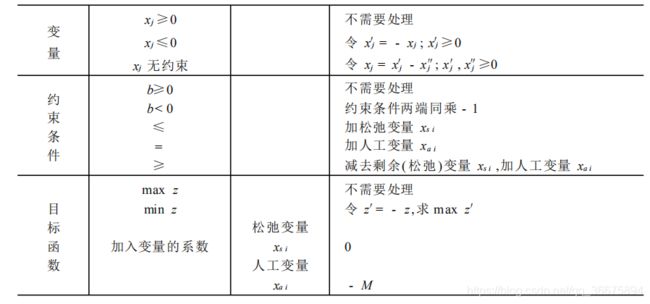
matlab 实现转化成标准形式的线性规划模型（因为拆分开，代码较长）。

clc;clear;close
%%  输入数据
decisionnum=1000;%决策变量的个数
limitnum=2000;%约束的个数
ambition=1;%1 :目标为Max, -1 :目标函数为Min
coef_C=round(rand(1,decisionnum)).*round(rands(1,decisionnum).*100);%约束的系数
coef_A=round(rand(limitnum,decisionnum)).*round(rands(limitnum,decisionnum).*100);%约束的系数
coef_B=round(rand(1,limitnum).*200);% 约束的右等式
limitrelation=round(rands(1,limitnum));% 是否是等式关系 -1：=《 ， 0 ：= = ， 1：= 
dicisionrelation=round(rands(1,decisionnum));% 决策变量的范围 -1=《0 ， 0 = 《》 ， 1= 》0
[standard,relation,error]=original2standard(ambition,decisionnum,limitnum,coef_A,coef_B,coef_C,limitrelation,dicisionrelation);
clear decisionnum limitnum coef_A coef_B coef_C limitrelation dicisionrelation
function [standard,relation,error]=original2standard(ambition,decisionnum,limitnum,coef_A,coef_B,coef_C,limitrelation,dicisionrelation)
% author:major-岩寐
% decisionnum 决策变量数量 limitnum约束条件限制个数
% coef_A 约束条件系数 coef_B右项式 coef_C决策变量系数 
% limitrelation 约束条件左项式和右项式的关系 -1：=《 ， 0 ：= = ， 1：= 》
% dicisionrelation 约束条件的取值-1=《0 ， 0 ：无界 ， 1=
% 》0（若决策变量大于或小于某值，根据取值范围来判断，譬如，x1>=-1,则将该约束写入约束条件，x1取值为无界
%默认 使用两阶段求解，来产生初始解，大M法不可靠在计算机里
tic
%% 1 转化决策变量
error=0;
n=0;%新的决策变量数量
newdecisionnum=decisionnum+sum(dicisionrelation==0);
stylend=zeros(1,newdecisionnum);%新的变量的状态，0为原变量，1为决策变量自身转化，2为约束条件的松弛或剩余变量，3人工变量
store=cell(1,decisionnum);
newcoef_A=zeros(limitnum,newdecisionnum);
newcoef_C=zeros(1,newdecisionnum);
for i=1:decisionnum %对每一个决策变量来讲
    switch dicisionrelation(i)
        case -1 % 如果小于等于0
            n=n+1;
            store{i}=[-1,n];
            newcoef_A(:,n)=coef_A(:,i).*-1;
            newcoef_C(n)=coef_C(i)*-1;
            stylend(n)=1;
        case 0
            n1=n+1;n2=n+2;n=n2;
            newcoef_A(:,n1)=coef_A(:,i);newcoef_A(:,n2)=coef_A(:,i).*-1;
            newcoef_C(n1)=coef_C(i);newcoef_C(n2)=coef_C(i).*-1;
            store{i}=[0,n1,n2];
            stylend(n1)=1;stylend(n2)=1;
        case 1
            n=n+1;
            newcoef_A(:,n)=coef_A(:,i);
            newcoef_C(n)=coef_C(i);
            store{i}=[1,n];
            stylend(n)=0;
        otherwise
            disp(' 抱歉，决策变量的设定为 -1:<=0 ， 0:无界 ， 1:>=0。决策变量设置有问题!')
            error=1;
    end
end
%% 2 转化目标函数 min
if ambition~=-1 %如果不是min
    newcoef_C=newcoef_C.*-1;
end
%% 3 转化右项式 以及 左右项式关系 先变动右项式再变动项式之间关系，不然松弛变量的系数为-1
intialcase=zeros(1,limitnum);
for i=1:limitnum
    if coef_B(i)<0% 如果右项式小于0 小于 后面的
        newcoef_A(i,n)=newcoef_A(i,n).*-1;coef_B(i)=coef_B(i).*-1;
    end
    if limitrelation(i)==-1
        n=n+1;
        newcoef_A(:,n)=zeros(limitnum,1);
        newcoef_A(i,n)=1;
        newcoef_C(n)=0;
        stylend(n)=2;
        intialcase(i)=n;
    elseif limitrelation(i)==0
        n=n+1;
        newcoef_A(:,n)=zeros(limitnum,1);
        newcoef_A(i,n)=1;
        newcoef_C(n)=0;
        stylend(n)=3;
        intialcase(i)=n;
    elseif limitrelation(i)==1
        n=n+1;
        newcoef_A(:,n)=zeros(limitnum,1);
        newcoef_A(i,n)=-1;
        newcoef_C(n)=0;
        stylend(n)=2;
        n=n+1;
        newcoef_A(:,n)=zeros(limitnum,1);
        newcoef_A(i,n)=1;
        newcoef_C(n)=0;
        stylend(n)=3;
        intialcase(i)=n;
    else
        disp(' 抱歉，约束变量的设定为-1: 左=< 右， 0 ：左== 右， 1：左>= 右。约束变量设置有问题')
        error=1;
    end
end
relation.store=store;relation.stylend=stylend;relation.intialcase=intialcase;
standard.decisionnum=n;standard.limitnum=limitnum;standard.coef_A=newcoef_A;standard.coef_B=coef_B;standard.coef_C=newcoef_C;
toc
end

至于为什么要转化成标准格式，在了解单纯形法的计算原理后便会清楚，所以不要急慢慢来（学数学、算法，心急是不行的）。
学习线性规划，需要先理解以下的证明。

1.若线性规划存在可行解则其可行解的集合为凸集合。

$$\begin{gathered} 假定凸集合为R^n,x^0,x^1\in R^n,x^0=\left\{x_1^0,x_2^0,\dots x_n^0\right\},x^1=\left\{x_1^1,x_2^1,\dots x_n^1\right\} \\ \mu \in \left[0,1\right]，x^2=x^0\times \mu +x^1\times \left(1-\mu \right)，x^2\in R^n \end{gathered}$$
即凸集合内每两个点连接的线段均在凸集合内，接下来以凸集合的概念推断于线性规划的几个证明。
$$\begin{gathered} \begin{array}{r}M:行数，N：列数，\forall i\in 1:M,\sum _{j=1}^n{A}_{ij}\times x_j^0=Bi,\sum _{j=1}^n{A}_{ij}\times x_j^1=Bi\end{array} \\ \forall i\in 1:M,\sum _{j=1}^n{A}_{ij}\times \left\{x_j^0\times \mu +x_j^1\times \left(1-\mu \right)\right\} \\ =\sum _{j=1}^n{A}_{ij}\times x_j^1+\mu \times \sum _{j=1}^n{A}_{ij}\times \left\{x_j^0-x_j^1\right\} \\ =\sum _{j=1}^n{A}_{ij}\times x_j^1+\mu \times \left\{\sum _{j=1}^n{A}_{ij}\times x_j^0-\sum _{j=1}^n{A}_{ij}\times x_j^1\right\} \\ =Bi+\mu \times \left\{Bi-Bi\right\}=Bi \end{gathered}$$
由上简单的拆分可以得到，在N维空间内，若有两点满足线规的约束，两点之间的任何一点同样满足。可以得到线性规划若有可行解则解集为凸集合。
**

2.线性规划的基可行解若存在必然是凸集合的顶点。

**
凸集合顶点的定义：若凸集合的某点不在集合内任何两点之间，则定义该点为顶点。
线性关系：即多个向量组P={p1，p2,…pn},其中p1为向量。判断是否存在不完全为0的A={a1，a2,…an},其中a1为一个数值。使得AP=0。（理解方式：通过高斯消元后若存在多个变量线性相加等于0，则该向量组呈线性关系，反之不为线性关系。典型的不是线性关系的为单位矩阵。
基可行解：是指定的m个决策变量，若该m列矩阵系数形成的向量组可以转化成单位矩阵，令其余的决策变量等于0，这样形成的一个解便是基可行解（书上不是这么定义的，但是理解后这样描述更加便于掌握）。
证明懒得写公式了，同样附上运筹学截图

上示公式描述：
若X为基可行解，假设X可以由其他的可行解线性X1,X2（X1-X2~=0，两者不完全相等）得到的话，则可以推导出X选定的m个决策变量对应的mm的向量组呈则呈线性关系，但是首先假定的是X为基可行解即其对应向量组呈非线性关系。推导出的结论和假定的结论矛盾，则可以得到结论：线性规划若存在可行解，其基可行解为顶点。
**

3.线性规划若存在最优解，该值等于某一顶点的目标值。

**
通过直角坐标系或者三维坐标系，目标函数是朝着一个方向前进，来理解很清晰。但为了数学的严谨性，同样进行证明。（同样截取运筹学课本上）

以上证明：若某一点不是顶点，肯定存在比他大或者小的点。

**

梳理一下，以上的逻辑

**
首先，线性规划问题若存在可行解，解集属于凸集。
再者，线性规划问题的基可行解为凸集的顶点
进而，线性规划的最优解必然为某一个顶点，（这句话有点不严谨，应该说线性规划的最优解的值必然与某个顶点的目标值一样，因存在无限多最优解，即某两个顶点都是最佳值，两点之间的所有点均为最佳值）
由上，如何解决线性规划就十分明确了。
第一步转化成标准形态，因为所有的推理均是以标准形态进行推导，
第二步找出初始基可行解。
第三步找出比当前基可行解要好的基可行解进行跳跃。课本上说的就是 换基的概念。
当然，专家需要用几十页来描述清除，我这简单的几千字自然不能描述的十分透彻。能帮助理解，自然十分开心。后续的下一次书写。