5.10 力扣 二叉搜索树 专题 671在议（没有利用节点值小于等于子节点的条件） 450 删除二叉搜索树中结点（利用前序，后继）

173 二叉搜索树迭代器：


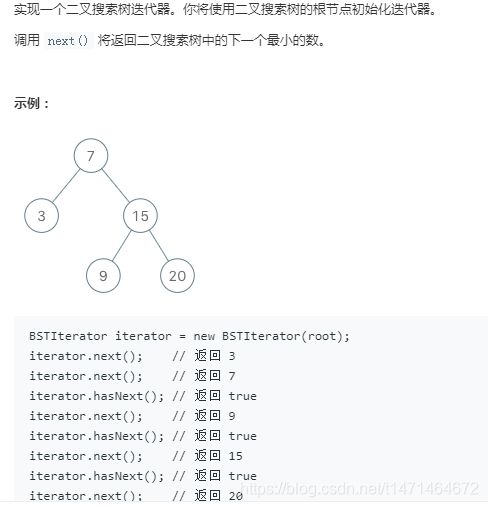
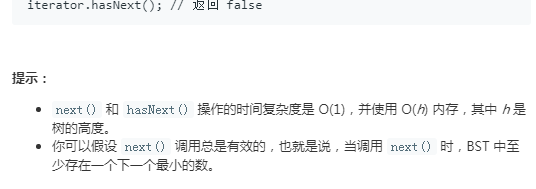
迭代器是使程序员能够遍历容器的对象。
hasNext()：若栈中还有元素，则返回 true，反之返回 false。所以这是一个 O(1)的操作
不符合题目要求：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class BSTIterator:

    def __init__(self, root: TreeNode):
        self.res=[]
        self.root=root
        node=self.root
        stack=[]
        while stack or node:
            while node:
                stack.append(node)
                node=node.left
            node=stack.pop()
            self.res.append(node.val)
            node=node.right
    def next(self) -> int:
        """
        @return the next smallest number
        """
        return self.res.pop(0)

    def hasNext(self) -> bool:
        """
        @return whether we have a next smallest number
        """
        return len(self.res)>=1
# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.next()
# param_2 = obj.hasNext()

采用迭代的方式来模拟中序遍历，而不是采用递归的方法；这样做的过程中，我们能够轻松的实现这两个函数的调用，而不是用其他额外的空间。
初始化一个空栈 S，用于模拟二叉搜索树的中序遍历。中序遍历我们采用与之前相同的方法，只是我们现在使用的是自己的栈而不是系统的堆栈。由于我们使用自定义的数据结构，因此可以随时暂停和恢复递归。
空间复杂度：O(h)，使用了一个栈来模拟递归

# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class BSTIterator:

    def __init__(self, root: TreeNode):
        self.current = root
        self.st = []

        
    def next(self) -> int:
        """
        @return the next smallest number
        """       
        while self.current or self.st:
            while self.current:
                self.st.append(self.current)
                self.current = self.current.left
            self.current = self.st.pop()
            node = self.current
            self.current = self.current.right
            return node.val

    def hasNext(self) -> bool:
        """
        @return whether we have a next smallest number
        """
        if self.st or self.current:
            return True
        return False
# Your BSTIterator object will be instantiated and called as such:
# obj = BSTIterator(root)
# param_1 = obj.next()
# param_2 = obj.hasNext()

530 二叉搜索树的最小绝对差
同783

class Solution:
    def getMinimumDifference(self, root: TreeNode) -> int:
        minmum=float('inf')
        stack=[]
        pre=float('-inf')
        while stack or root:
            while root:
                stack.append(root)
                root=root.left
            root=stack.pop()
            minmum=min(minmum,abs(root.val-pre))
            pre=root.val
            root=root.right
        return minmum

532. 数组中的K-diff数对

哈希表对数据去重：

class Solution:
    def findPairs(self, nums: List[int], k: int) -> int:
        if not nums or k<0:
            return 0
        hash={}
        count=0
        for i in range(len(nums)):
            if nums[i] not in hash:
                hash[nums[i]]=1
            else:
                hash[nums[i]]+=1
        if k==0:
            for i in hash:
                if hash[i]>1:
                    count+=1
        elif k>0:
            for i in hash:
                if i+k in hash:
                    count+=1
        return count 

230 二叉搜索树中第K小元素

class Solution:
    def kthSmallest(self, root: TreeNode, k: int) -> int:
        if not root:
            return 
        stack=[]
        while stack or root:
            while root:
                stack.append(root)
                root=root.left
            root=stack.pop()
            k-=1
            if k==0:
                return root.val
            root=root.right

671. 二叉树中第二小的节点

时间复杂度 空间复杂度均为O（n）
没有利用

class Solution:
    def findSecondMinimumValue(self, root: TreeNode) -> int:
        def dfs(root):
            if not root:
                return []
            return [root.val]+dfs(root.left)+dfs(root.right)
        res=dfs(root)      
        res=list(set(res))
        res.sort()
        return res[1] if len(res)>=2 else -1

672. 两数之和 IV - 输入 BST

中序遍历
递归：

class Solution:
    def findTarget(self, root: TreeNode, k: int) -> bool:
        self.target=k
        self.ans=False
        self.hash=set()
        def dfs(root):
            if not root:
                return False
            dfs(root.left)
            #self.ans剪枝
            if self.target-root.val in self.hash and not self.ans:
                self.ans=True 
                return 
            self.hash.add(root.val)
            dfs(root.right)
        dfs(root)
        return self.ans

迭代：

class Solution:
    def findTarget(self, root: TreeNode, k: int) -> bool:
        if not root:
            return False
        stack=[]
        visit=set()
        while stack or root:
            while root:
                stack.append(root)
                root=root.left
            root=stack.pop()
            if k-root.val in visit:
                return True
            visit.add(root.val)
            root=root.right
        return False

673. 两数之和 II - 输入有序数组

双指针法：

class Solution:
    def twoSum(self, numbers: List[int], target: int) -> List[int]:
        i,j=0,len(numbers)-1
        res=[]
        while i<j:
            if numbers[i]+numbers[j]==target:
                res.extend([i+1,j+1])
                return res
            elif numbers[i]+numbers[j]<target:
                i+=1
            elif numbers[i]+numbers[j]>target:
                j-=1
       return [-1,-1]

二叉搜索树中复杂度为对数时间的操作：查找 插入 删除
450 删除二叉搜索树中的节点


（一） 按情况分类解法 算法思想
1 检索要删除的节点p，并在检索的过程中记录其父结点par。
2 删除节点
假设已经确定应该删除节点p,它是其父节点par的左子节点。（为右子节点的情况类似）
（1）如果p为叶子节点，直接删除。即令par的左子节点为空。
（2）如果p.left为空树，这事只需把p的右子树改为其父结点par的左子树。
（3）p有左子树，这时先找到p的左子树的最右节点，设为r,显然它没有右子树。用p的左子节点代替par的左子节点，并将p的右子树作为r的右子树。

# 该方法是将删除节点的右子树加到删除节点的左子树的后面
class Solution:
    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        p=root
        pre=None
        while p:
            if key<p.val:
                pre=p
                p=p.left
            elif key>p.val:
                pre=p
                p=p.right
            else:
                #p是叶子结点
                if not p.left and not p.right:
                    #p是根节点，且无子树
                    if pre==None:
                        root=None
                    else:
                        #p是pre的左叶子节点
                        if key<pre.val:
                            pre.left=None
                        #p是pre的右叶子结点
                        else:
                            pre.right=None
                elif not p.left:
                    #如果只有右子树，则直接将p的右子树接到pre上
                    if pre==None:
                        root=p.right
                    else:
                        if key<pre.val:
                            pre.left=p.right
                        else:
                            pre.right=p.right
                else:
                    #存在左子树
                    #找到p的左子树中最大的点，即递增序列中p前面的点，即比p小的值中的最大值，即p的前序节点
                    r=p.left
                    while r.right:
                        r=r.right
                    #说明p是根节点，将p的左子树作为新的根节点，右子树加到根节点在递增序列中的前一个点的右边
                    if pre==None:
                        r.right=p.right
                        root=p.left
                    else:
                        #p不是根节点，且位于父节点的左侧
                        if key<pre.val:
                            pre.left=p.left
                            r.right=p.right
                        else:
                        #p不是根节点，且位于父节点的右侧
                            pre.right=p.left
                            r.right=p.right
                #找到这样的p
                return root
        #遍历完还没找到，返回原来root
        return root

二叉搜索树的前驱节点：
对于前驱，节点要有左子树；对于后继，节点要有右子树。
代表的是中序遍历序列的前一个节点。即比当前节点小的最大节点，简称前驱节点。先取当前节点的左节点，然后取该节点的右节点，直到右节点为空，则最后指向的节点为前驱节点。
如果不存在左子树，则该节点的前驱节点在节点之上面，不方便迭代向下删除

#当存在左子树时
def predecessor(root):
    root = root.left
    while root.right:
        root = root.right
    return root

二叉搜索树的后继节点：
中序遍历序列的下一个节点。即比当前节点大的最小节点，简称后继节点。 先取当前节点的右节点，然后一直取该节点的左节点，直到左节点为空，则最后指向的节点为后继节点。
该后继节点位于右子树中较低的位置。然后可以从后继节点的位置递归向下操作以删除后继节点。
如果该节点不存在右子树时，该方法不成立，因为此时节点的后继节点在其上面

##当存在右子树时
def successor(root):
    root = root.right
    while root.left:
        root = root.left
    return root

（二）递归解法：
不是删除该节点，而是用其后继或前驱节点值替换，然后递归删除其后继或前驱节点
速度比分情况讨论慢
算法思想：
1.当Key大于当前节点值，则说明需要删除的节点位于当前节点右子树
2.当Key小于当前节点值，则说明需要删除的节点位于当前节点左子树
3。当key等于当前节点值
1.若当前节点为叶子结点，则直接赋值None
2.若当前节点存在右子树，则按照二叉搜素树中序性质，其后继节点在右子树中，用后继节点值替换当前节点值，然后递归删除后继节点
3.若当前节点不存在右子树单存在左子树，则后继节点在当前节点上面或者不存在，前序节点在左子树中，则可以用前序节点值替换，递归删除前序节点值

class Solution:
    #后继节点
    def successor(self,root):
        root=root.right
        while root.left:
            root=root.left
        return root.val
    #前驱节点
    def predecessor(self,root):
        root=root.left
        while root.right:
            root=root.right
        return root.val
    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        if not root:
            return 
        #  要删除的节点在右子树
        if key>root.val:
            root.right=self.deleteNode(root.right,key)
        # 要删除的节点在左子树
        elif key<root.val:
            root.left=self.deleteNode(root.left,key)
        # 找到需要删除的节点
        else:
            #叶子结点直接赋值None
            if not root.left and not root.right:
                root=None
            # 存在右子树（左子树存不存在都可以），用后继节点值替换，然后递归向下删除右子树中的后继节点
            elif root.right:
                root.val=self.successor(root)
                root.right=self.deleteNode(root.right,root.val)
            # 只存在左子树，用前驱节点值替换，然后删除左子树中的前驱节点
            # 要删除的节点不是叶子节点，且没有右节点但是有左节点。这意味着它的后继节点在它的上面，但是我们并不想返回。我们可以使用它的前驱节点进行替代，然后再递归的向下删除前驱节点。
            elif root.left:
                root.val=self.predecessor(root)
                root.left=self.deleteNode(root.left,root.val)
        return root

700. 二叉搜索树中的搜索


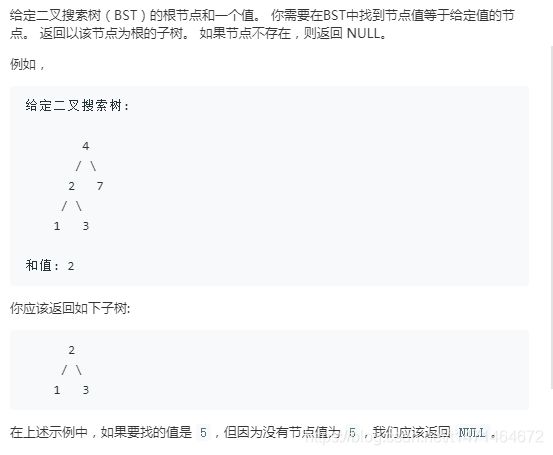
迭代比递归空间复杂度低
迭代：

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
    	p=root
        if not p:
            return 
        while p:
            if p.val<val:
                p=p.right
            elif p.val>val:
                p=p.left
            else:
                return p
        return None

递归：

class Solution:
    def searchBST(self, root: TreeNode, val: int) -> TreeNode:
        if not root:
            return 
        if root.val<val:
            return self.searchBST(root.right,val)
        elif root.val>val:
            return self.searchBST(root.left,val)
        else:
            return root

701 二叉搜索树的插入操作：

迭代：
1如果二叉搜索树为空树，用val构造二叉树节点作为根节点并返回。
2否则，搜索新结点的插入位置，沿子结点关系向下：
遇到应该走向左子树而左子树为空，或者应该走向右子树而右子树为空时，就是找到了新字典项的插入位置，构造新结点并完成实际插入。
之后，返回根节点。

class Solution:
    def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
        p=TreeNode(val)
        if not root:
            return p
        node=root
        #插入到右子树
        while node:
            if node.val<val:
                if node.right:
                    node=node.right
                else:
                    node.right=p
                    return root
            else:
                if node.left:
                    node=node.left
                else:
                    node.left=p
                    return root

递归：

class Solution:
    def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
        p=TreeNode(val)
        if not root:
            return p
        #插入到右子树
        if root.val<val:
        	root.right=self.insertIntoBST(root.right,val)
        else:
            root.left=self.insertIntoBST(root.left,val)
        return root

1305 两棵二叉搜索树中所有元素

class Solution:
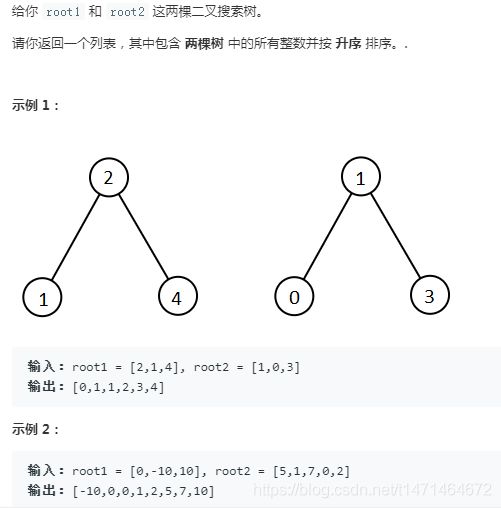
    def getAllElements(self, root1: TreeNode, root2: TreeNode) -> List[int]:
        def dfs(root):
            if not root:
                return []
            return dfs(root.left)+[root.val]+dfs(root.right)
        res1=dfs(root1)
        res2=dfs(root2)
        n1,n2=len(res1),len(res2)
        res=[]
        i,j=0,0
        while i<n1 and j<n2:
            if res1[i]<res2[j]:
                res.append(res1[i])
                i+=1
            else:
                res.append(res2[j])
                j+=1
        if j==n2:
            res.extend(res1[i:]) 
        else :
            res.extend(res2[j:])
        return res

面试题33 二叉搜索树的后序遍历序列

后序遍历 根节点在最后
在数组中从后往前第一个小于根节点的数值，前面的都是左子树，后面的都是右子树，依次递归判断，一旦某部分不符合条件，则说明不是二叉搜索树
自己的写法：

class Solution:
    def verifyPostorder(self, postorder):

        if len(postorder)<=1:
            return True
        root=postorder[-1]
        index=-1
        #找到左右子树分割点index
        for i in range(len(postorder)-2,-1,-1):
            if postorder[i]<root:
                index=i
                break
        flag1,flag2=True,True
        #判断左子树数据是否都小于根节点
        for pos in postorder[:index+1]:
            if pos>root:
                flag1=False
         #判断右子树数据是否都大于根节点
        for pos in postorder[index+1:-1]:
            if pos<root:
                flag2=False
        return flag1 and flag2 and self.verifyPostorder(postorder[:index+1]) and self.verifyPostorder(postorder[index+1:-1])

题解写法：

class Solution:
    def verifyPostorder(self, postorder: [int]) -> bool:
        def recur(i, j):
            if i >= j: return True
            p = i
            while postorder[p] < postorder[j]: 
            	p += 1
            #找到左右子树分割点
            # 从左到右 第一个大于根节点 的节点
            m = p
            while postorder[p] > postorder[j]: 
            	p += 1
            #每次取出一个根节点
            return p == j and recur(i, m - 1) and recur(m, j - 1)
        return recur(0, len(postorder) - 1)