力扣 5.21 单调栈
回文串、最长公共子串系列
5 最长回文子串
动态规划,dp[i][j]=True表示i-j之间是回文串
如果dp[i+1][j-1]==True 且s[i]==s[j],那么说明dp[i][j]也是回文串,可以更新最大长度
如果s[i]==s[j]且j-i<=2,说明该字符串是bb或者aba型,也是回文串
class Solution: def longestPalindrome(self, s: str) -> str: n=len(s) if n<=1: return s maxl,l,r=0,0,0 dp=[[False]*n for _ in range(n)] for j in range(1,n): for i in range(j): if s[i]==s[j] and (j-i<=2 or dp[i+1][j-1]): dp[i][j]=True if j-i+1>maxl: maxl=max(j-i+1,maxl) l,r=i,j return s[l:r+1]
414. 第三大的数

排序的时间复杂度是O(nlogn)
优先队列(复杂度O(nlg3))
时间复杂度为O(n),因此需要一次遍历,用三个数保存数组的前三大数字
空间复杂度为O(1)
class Solution:
def thirdMax(self, nums: List[int]) -> int:
a=b=c=float('-inf')
for i in nums:
if i>a:
c=b
b=a
a=i
elif i>b and i!=a:
c=b
b=i
elif i>c and i!=b and i!=a:
c=i
return c if c!=float('-inf') else a
单调栈
主要解决下面的问题:
比当前元素更大的下一个元素
比当前元素更大的前一个元素
比当前元素更小的下一个元素
比当前元素更小的前一个元素
单调递增栈:数据出栈的序列为单调递增序列
当数据入栈时,如果栈为空或者入栈元素小于栈顶元素,则入栈
否则入栈则会破坏栈的单调性,则需要把比入栈元素小的元素全部出栈,单调递减则相反
单调递减栈:数据出栈的序列为单调递减序列
907. 子数组的最小值之和

如果求出包含A[i]并以A[i]为最小元素的所有子数组个数n[i],则元素A[i]对答案ans的贡献为n[i]A[i]
维护一个单调递增栈,遍历数组每个元素A[i],存进去的的是左边第一个小于该元素的元素下标left,右边第一个小于该元素的元素下标right,以A[i]为最小元素的所有子数组的个数为n[i]=(i-left)*(right-i)(这个子数组左边有i-left个端点可以选择,右边有right-i个端点可以选择
维护一个单调递增栈,当遇到一个元素A[a]
为了保证所有元素都能被弹出,两端增加两个float(’-inf’)
时间复杂度O(N),空间复杂度O(N)

class Solution:
def sumSubarrayMins(self, A: List[int]) -> int:
#一遍遍历,边遍历边计算
# A=[float('-inf')]+A+[float('-inf')]
# stack=[]
# ans=0
# for i in range(len(A)):
# while stack and A[stack[-1]]>A[i]:
# cur=stack.pop()
# ans+=A[cur]*(cur-stack[-1])*(i-cur)
# stack.append(i)
# return ans%(10**9+7)
#两遍遍历
left=[0]*len(A)
right=[0]*len(A)
stack=[]
#从左往右记录左边第一个小于该元素的下标
#从左往右维护一个单调递增栈
for i in range(len(A)):
while stack and A[stack[-1]]>A[i]:
stack.pop()
if not stack:
left[i]=-1
else:
left[i]=stack[-1]
stack.append(i)
stack=[]
#从右往左记录右边第一个小于该元素的下标
#从右往左维护一个单调递增栈
for i in range(len(A)-1,-1,-1):
while stack and A[stack[-1]]>=A[i]:
stack.pop()
if not stack:
right[i]=len(A)
else:
right[i]=stack[-1]
stack.append(i)
ans=0
for i in range(len(A)):
ans+=A[i]*(i-left[i])*(right[i]-i)
ans%=10**9+7
return ans
class Solution:
def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
#从右往左维护一个单调递增栈
stack=[]
# right=[0]*len(nums2)
right=defaultdict(int)
for i in range(len(nums2)-1,-1,-1):
while stack and stack[-1]<nums2[i]:
stack.pop()
if not stack:
# right[i]=-1
right[nums2[i]]=-1
else:
# right[i]=stack[-1]
right[nums2[i]]=stack[-1]
stack.append(nums2[i])
res=[]
for num in nums1:
# idx=nums2.index(num)
# res.append(right[idx])
res.append(right[num])
return res
class Solution:
def nextGreaterElements(self, nums: List[int]) -> List[int]:
stack=[]
res=[0]*len(nums)
for i in range(2*len(nums)-1,-1,-1):
#从右向左,如果当前元素比栈顶元素小,说明当前元素的下一个更大元素就是栈顶元素,同时把当前元素添加进去,从栈顶到栈底是递增的,即新添加的元素要小于之前栈顶元素
#如果当前元素比栈顶元素还大,要弹出栈中小于等于当前元素,弹完之后的栈顶元素就是当前元素右边的下一个更大元素
while stack and stack[-1]<=nums[i%len(nums)]:
stack.pop()
if not stack:
res[i%len(nums)]=-1
else:
res[i%len(nums)]=stack[-1]
stack.append(nums[i%len(nums)])
return res
84. 柱状图中最大的矩形


单调递增栈:
要求:如果新的元素比栈顶元素大,就入栈, 如果新的元素较小,那就一直把栈内元素弹出来,直到栈顶比新元素小
特点:栈内的元素是递增的,
当元素出栈时,说明这个新元素是出栈元素向后(右边)找第一个比其小的元素,
当元素出栈后,说明新栈顶元素是出栈元素向前(左边)找第一个比其小的元素
对于一个高度,如果能得到向左和向右的边界
那么就能对每个高度求一次面积
遍历所有高度,即可得出最大面积
使用单调递增栈,在出栈操作时得到前后边界并计算面积
class Solution:
def largestRectangleArea(self, heights: [int]) -> int:
maxr=0
stack=[]
#右边添加哨兵元素,保证栈内所有数据都可以被弹出,因为矩形高度都是正数
heights.append(0)
#维护一个单调递增栈,同时更新最大面积
# 当heights[i]小于栈顶元素时,以栈顶元素为高的矩形已不能继续向右延申(达到右边界)。
# 矩形左边界就是栈顶元素的前一个元素。
#弹出一个高度时,找到这个高度左边第一个比其小的元素(新栈顶),右边第一个比其小的元素(当前元素),两个下标的差值-1即为该高度的宽度
#所以宽是i-left-1
for i in range(len(heights)):
while stack and heights[stack[-1]]>=heights[i]:
h=heights[stack.pop()]
left=stack[-1] if stack else -1
maxr=max(maxr,(i-left-1)*h)
stack.append(i)
return maxr
42 接雨水

雨水是按照颜色分层相加的,通过弹出栈顶元素实现
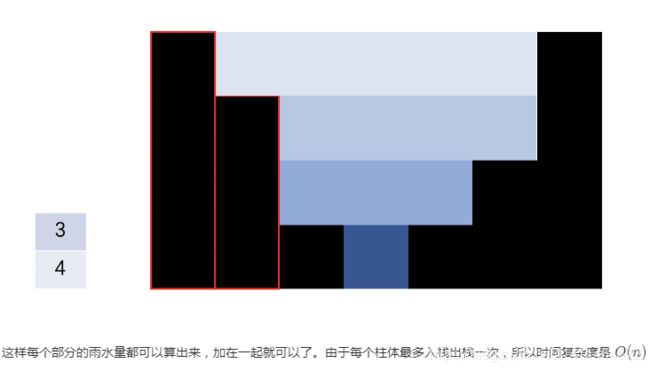
木桶效应
走到最后栈内可以留有柱子,单调递减也接不了雨水,不需要设置哨兵元素
class Solution:
def trap(self, height: List[int]) -> int:
if len(height)<3:
return 0
#维护单调不增栈/单调递减栈
stack=[]
ans=0
for i in range(len(height)):
#新元素是弹出元素右边第一个更大的值
#此时栈顶元素是弹出元素左边第一个更大的值
#凹槽的高度是左右两边更大值的较小值-弹出的栈顶(这个栈顶是三个数中最小的)
#这里加不加等号一样
while stack and height[i]>=height[stack[-1]]:
tmp=stack.pop()
ans+=(min(height[stack[-1]],height[i])-height[tmp])*(i-stack[-1]-1) if stack else 0
stack.append(i)
return ans
class Solution:
def dailyTemperatures(self, T: List[int]) -> List[int]:
res=[0]*len(T)
stack=[]
# #从右向左维护一个递减栈,如果当前元素大于栈顶元素,将当前元素加入栈会破坏单调性,此时将栈中小于当前元素的值都弹出,最后剩的栈顶元素就是当前元素右边第一个更大温度
# for i in range(len(T)-1,-1,-1):
# while stack and T[stack[-1]]<=T[i]:
# stack.pop()
# #从右往左是递减栈,当前元素的右边第一个更大值都是当前的栈顶元素
# if stack:
# res[i]=stack[-1]-i
# stack.append(i)
# return res
#从左往右,维护一个非严格单调递减栈,当前元素大于栈顶元素时,栈顶元素右边第一个更大元素就是当前元素
for i in range(len(T)):
while stack and T[stack[-1]]<T[i]:
cur=stack.pop()
res[cur]=i-cur
stack.append(i)
return res
class StockSpanner:
def __init__(self):
# 存储栈顶价格和下标
#(float('inf'),0) 为了使输入的第一个价格有输出
self.stack=[(float('inf'),0)]
#保留这是第几次输入的信息
self.count=0
def next(self, price: int) -> int:
self.count+=1
res=1
#当前价格大于等于栈顶元素时,栈顶元素都要弹出,比如(100,1)(80,2),(75,6),当遇到(80,7)时,从2开始到7都是符合小于等于今日价格条件的,总共有6个数,应弹出元素,使栈顶元素为100,1,7-1=6
#维持严格单调递减栈
while self.stack and price>=self.stack[-1][0]:
self.stack.pop()
if self.stack:
res=self.count-self.stack[-1][1]
self.stack.append((price,self.count))
return res
# Your StockSpanner object will be instantiated and called as such:
# obj = StockSpanner()
# param_1 = obj.next(price)
1019. 链表中的下一个更大节点


法一:数组保存链表节点,维护一个单调递减栈,当前元素就是栈顶元素的下一个更大值
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def nextLargerNodes(self, head: ListNode) -> List[int]:
cur=tmp=head
count=0
ans=[]
while tmp:
count+=1
ans.append(tmp.val)
tmp=tmp.next
#单调递减栈
res=[0]*count
stack=[]
for i in range(count):
while stack and ans[i]>ans[stack[-1]]:
idx=stack.pop()
res[idx]=ans[i]
stack.append(i)
return res
法二:直接操作链表
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, x):
# self.val = x
# self.next = None
class Solution:
def nextLargerNodes(self, head: ListNode) -> List[int]:
# 直接操作链表,需要两个栈,一个存下标,一个存数据
stack=[]
stack_loc=[]
res=[]
loc=-1
while head:
#保证结果数组长度与链表长度一致,需要修改数据用下标修改
res.append(0)
loc+=1
while stack and stack[-1]<head.val:
res[stack_loc[-1]]=head.val
stack.pop()
stack_loc.pop()
stack.append(head.val)
stack_loc.append(loc)
head=head.next
return res
class Solution:
def buildArray(self, target: List[int], n: int) -> List[str]:
res=[]
#start表示到哪个数字了
start=1
for i in range(len(target)):
#当前数字小于目标值,那么推入后弹出,当前数字加1
while start<target[i]:
res.extend(['Push','Pop'])
start+=1
#当前数字等于目标值,推入即可,当前数字往下走
if start==target[i]:
res.append('Push')
start+=1
return res








