力扣入职第一周，啥也不是呜呜呜呜

297. 二叉树的序列化与反序列化

前序遍历

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Codec:

    def serialize(self, root):
        """Encodes a tree to a single string.
        
        :type root: TreeNode
        :rtype: str
        """
        if not root:
            return 'None'
        return str(root.val)+','+self.serialize(root.left)+','+self.serialize(root.right)
    def deserialize(self, data):
        """Decodes your encoded data to tree.
        
        :type data: str
        :rtype: TreeNode
        """
        def dfs(l):
            node=l.pop(0)
            if node=='None':
                return None
            root=TreeNode(node)
            root.left=dfs(l)
            root.right=dfs(l)
            return root
        l=data.split(',')
        return dfs(l)

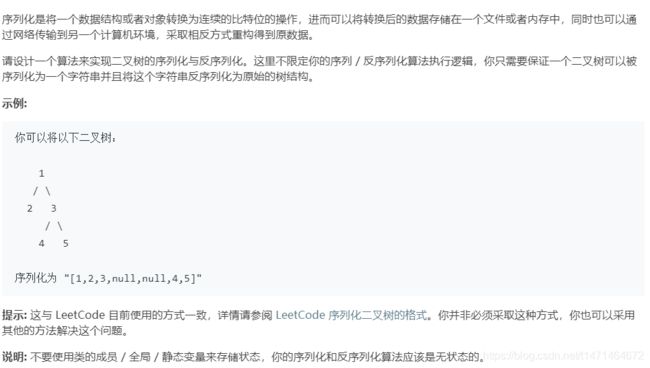
层次遍历

# Definition for a binary tree node.
# class TreeNode(object):
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Codec:

    def serialize(self, root):
        """Encodes a tree to a single string.
        
        :type root: TreeNode
        :rtype: str
        """
        if not root:
            return '[]'
        queue=deque()
        queue.append(root)
        res=[]
        while queue:
            for _ in range(len(queue)):
                node=queue.popleft()
                if node:
                    res.append(str(node.val))
                    queue.append(node.left)
                    queue.append(node.right)
                else:
                    res.append('null')
        return '['+','.join(res)+']'

    def deserialize(self, data):
        """Decodes your encoded data to tree.
        
        :type data: str
        :rtype: TreeNode
        """
        if data=='[]':
            return None
        l=data[1:-1].split(',')
        i=1
        root=TreeNode(l[0])
        queue=deque()
        queue.append(root)
        while queue:
            node=queue.popleft()
            if l[i]!='null':
                node.left=TreeNode(l[i])
                queue.append(node.left)
            i+=1
            if l[i]!='null':
                node.right=TreeNode(l[i])
                queue.append(node.right)
            i+=1
        return root

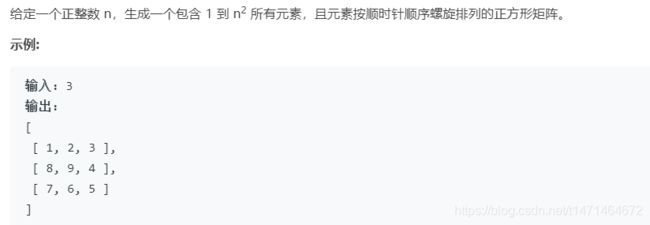
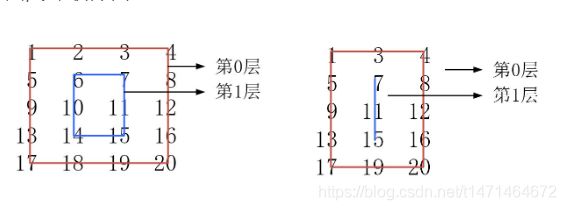
54. 螺旋矩阵

按层模拟：每一层有两行,两列,一行一列,好几种组合
每层
从左到右， matrix[i][j]：j: i–n-i
从上到下，matrix[j][n-i]：j: i+1–m-i
从右到左，要判断这层是否只有一行，即m-1-i !=i,matrix[m-1-i ][j] :j : n-1-(i+1)–i
从下到上:要判断这层是否只有一列，即 n-1-i!=i, matrix[j][i] j: m-1-(i+1): i+1

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        if not matrix:
            return []
        m,n=len(matrix),len(matrix[0])
        i=0
        res=[]
        #层数
        count=(min(m,n)+1)//2
        while i<count:
            for j in range(i,n-i):
                res.append(matrix[i][j])
            for j in range(i+1,m-i):
                res.append(matrix[j][n-1-i])
            if m-1-i!=i:
                for j in range(n-1-(i+1),i-1,-1):
                    res.append(matrix[m-1-i][j])
            if n-1-i!=i:
                for j in range(m-1-(i+1),i,-1):
                    res.append(matrix[j][i])
            i+=1
        return res

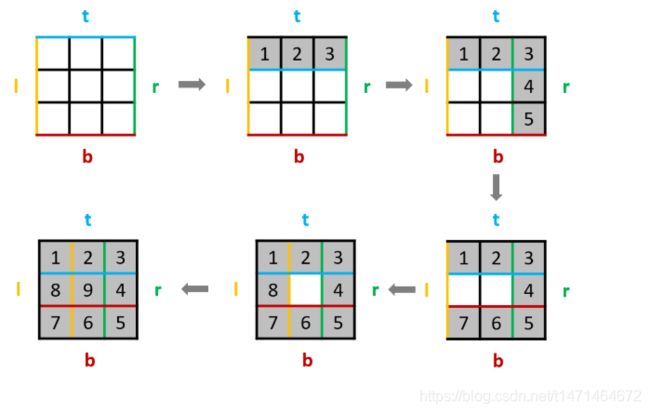
法二：设置四个边界
一层层向里处理，按顺时针依次遍历：上、右、下、左层
不再形成“环”了，就会剩下一行或一列，然后单独判断
l,r,t,b=0,n-1,0,m-1

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        if not matrix:
            return []
        m,n=len(matrix),len(matrix[0])
        l,r,t,b=0,n-1,0,m-1
        res=[]
        while l<r and t<b:
            for j in range(l,r):
                res.append(matrix[t][j])
            for i in range(t,b):
                res.append(matrix[i][r])
            for j in range(r,l,-1):
                res.append(matrix[b][j])
            for i in range(b,t,-1):
                res.append(matrix[i][l])
            l+=1
            r-=1
            t+=1
            b-=1
        if t==b:
            for j in range(l,r+1):
                res.append(matrix[t][j])
        elif l==r:
            for i in range(t,b+1):
                res.append(matrix[i][l])
        return res

59. 螺旋矩阵 II

class Solution:
    def generateMatrix(self, n: int) -> List[List[int]]:
        l,r,t,b=0,n-1,0,n-1
        num=1
        res=[[0]*n for i in range(n)]
        while num<=n*n:
            for j in range(l,r+1):
                res[t][j]=num
                num+=1
            t+=1
            for i in range(t,b+1):
                res[i][r]=num
                num+=1
            r-=1
            for j in range(r,l-1,-1):
                res[b][j]=num
                num+=1
            b-=1
            for i in range(b,t-1,-1):
                res[i][l]=num
                num+=1
            l+=1
        return res

115. 不同的子序列


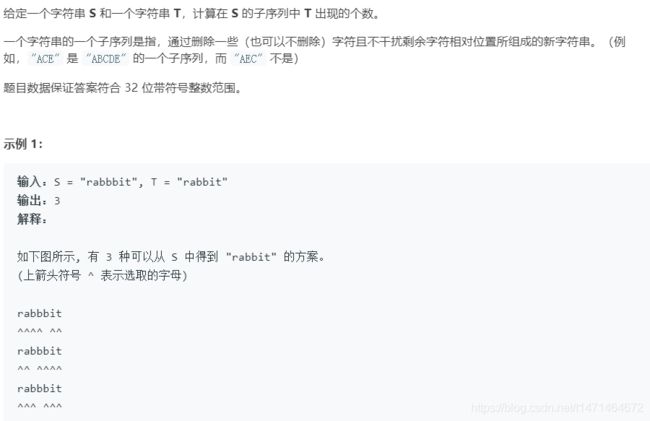
dp[i][j]代表s[:j]的子序列中t[:i]出现的个数
if s[i]==t[j] dp[i][j]=dp[i−1][j]+dp[i−1][j−1]
S[j] != T[i] , dp[i][j] = dp[i][j-1]
给二维dp增加两个边界，表示为空的情况

特殊情况：
如果T为空集，空集是所有字符串子集，dp[0][j]=1
如果S为空集，则dp[i][0]=0

class Solution:
    def numDistinct(self, s: str, t: str) -> int:
        m,n=len(s),len(t)
        dp=[[0]*(m+1) for i in range(n+1)]
        dp[0][0]=1
        for j in range(1,m):
            dp[0][j]=1
        for i in range(1,n+1):
            for j in range(1,m+1):
                if s[j-1]==t[i-1]:
                    dp[i][j]=dp[i-1][j-1]+dp[i][j-1]
                else:
                    dp[i][j]=dp[i][j-1]
        return dp[-1][-1]

1025. 除数博弈

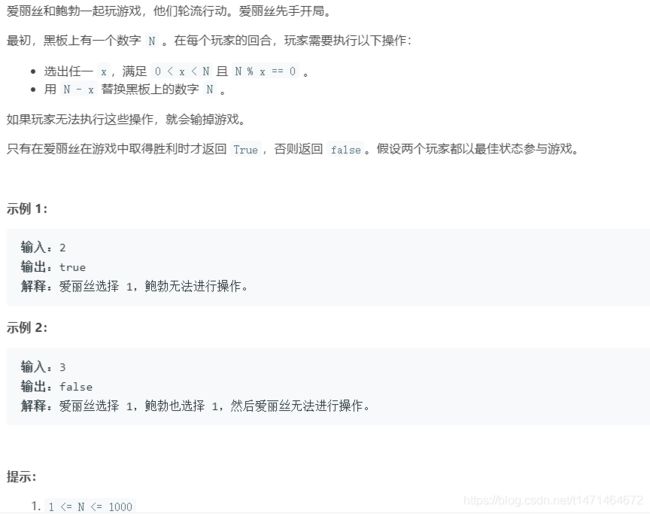
归纳法 ：
从该数倒着往前
奇数的约数只能为1或者奇数，那么下一个数一定是偶数
偶数的约数可以是1或偶数或者奇数，那么偶数直接减一，是奇数
所以奇数输了，偶数赢

class Solution:
    def divisorGame(self, N: int) -> bool:
        return N%2==0

动态规划：
p[i]=false:当前用户选择范围是0-i,则没有可操作的数字，将输掉比赛
p[1]=false,当前数字为1，没有可选择数字，则输掉比赛
p[2]=True,当前数字为2，p[2-1]=p[1]=false,所以对方输掉比赛，则p[2]=true

class Solution:
    def divisorGame(self, N: int) -> bool:
        p=[False]*(N+1)
        for i in range(2,N+1):
            for j in range(1,i):
                if i%j==0:
                    if p[i-j]==False:
                        p[i]=True
        return p[-1]

462. 最少移动次数使数组元素相等 II

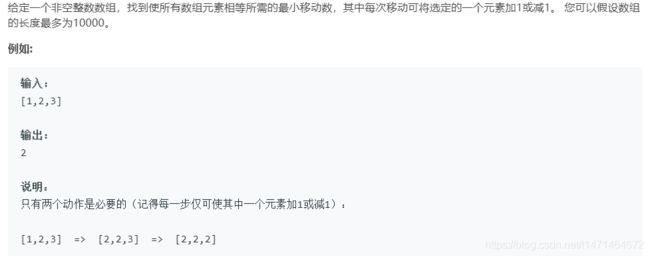
排序后寻找中位数
目的是使这些数到一个数x的距离之和最小
设 a <= x <= b，将 a 和 b 都变化成 x 为最终目的，则需要步数为 x-a+b-x = b-a，即两个数最后相等的话步数一定是他们的差，x 在 a 和 b 间任意取；
所以最后剩的其实就是中位数；
那么直接排序后首尾指针计算就好

class Solution:
    def minMoves2(self, nums: List[int]) -> int:
        nums.sort()
        ans=0
        i,j=0,len(nums)-1
        while i<j:
            ans+=nums[j]-nums[i]
            i+=1
            j-=1
        return ans

class Solution:
    def minMoves2(self, nums: List[int]) -> int:
        nums.sort()
        ans=0
        for num in nums:
            ans+=abs(nums[len(nums)//2]-num)
        return ans

453. 最小移动次数使数组元素相等

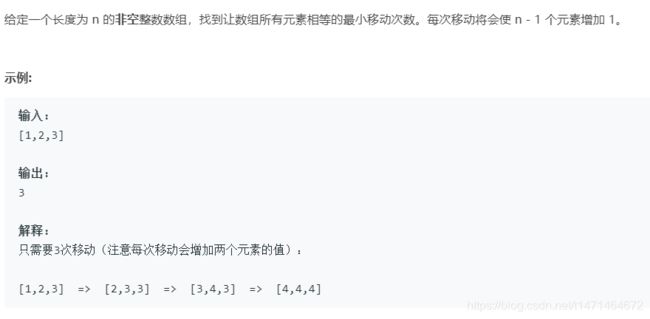
为了在最小移动内使所有元素相等，我们需要在数组的最大元素之外的所有元素中执行增加。每次用用 diff=max-min 更新数列，排序后，第一次最小值是a[0],最大值是a[n-1],除a[n-1]外的所有数都要增加diff，diff=a[n-1]-a[0],a[0]变为a[n-1],此时最小值还是a[0],最大值变为a[n-2]，依次迭代，因为每次移动只增加元素1，所以每次加上diff次移动
每一次用最大最小差值移动数组，
虽然每一步都会更新数组中的值，但是每次最大最小数差值和原来数组保持一致，因为每次max和min数增加的值一致
第一次：a[0]=a[0]+(a[n-1]-a[0]) a[n-2]=a[n-2]+(a[n-1]-a[0])
第二次：
最小值是a[0],最大值是a[n-2],diff=a[n-2]-a[0]=a[n-2]-a[0]
换个角度：
每次移动一个数，另外n-1个数+1，换个角度，每次移动一个数，这个数就减一。所以所有数字与数组中最小值的差值的和就是最小移动次数

class Solution:
    def minMoves(self, nums: List[int]) -> int:
        nums.sort()
        ans=0
        for i in range(len(nums)-1,0,-1):
            ans+=nums[i]-nums[0]
        return ans 

29 两数相除

class Solution:
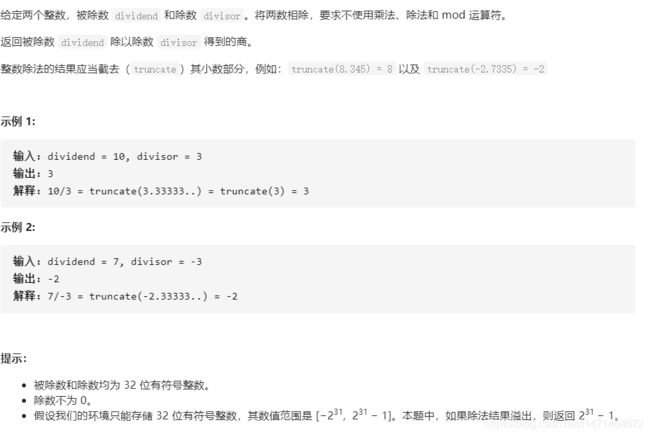
    def divide(self, dividend: int, divisor: int) -> int:
        #除法的意思就是被除数中含有几个除数，如果每次只减去一个除数来计算商，会超时，所以直接找到几倍的除数最接近被除数，然后在缩小范围
        res=0
        flag=(dividend>0)^(divisor>0)
        dividend=abs(dividend)
        divisor=abs(divisor)
        count=0 #记录减去多少除数，即为商
        #左移除数，直到除数大于被除数
        while divisor<=dividend:
            count+=1
            divisor<<=1
        while count>0:
            count-=1
            divisor>>=1
            #count代表着此时除数左移了几位，即扩大了几个2倍，res加上这个倍数，即表示被除数中有几个除数
            if divisor<=dividend:
                #比如count=2,即左移了2位，即100，相当于扩大4倍，需要加上这个倍数的十进制数
                res+=1<<count
                dividend-=divisor
        if flag:
            res=-res
        return res if -(1<<31)<=res<=(1<<31)-1 else (1<<31)-1

10. 正则表达式匹配


:可以匹配前面字符0次，一次，多次
dp[i][j]=True:表示s的前I个字符与p的前j个字符匹配
dp[0][0]=True:如果两个字符串都是空的，则匹配
dp[0][j]=dp[0][j-2]:可以表示前面字符匹配0次，则可以忽略j,j-1两个字符，直接状态与j-2匹配
情况1：如果第j个字符是‘’：则需要判断j前面一个字符是否与s的第i个字符匹配，如果匹配，说明是无s第i个字符状态，则此时状态依赖于dp[i-1][j],因为可以匹配多次前面那个字符，接着判断s的前i-1个字符与p的前J个字符的状态，总结一下对应状态即dp[i]j-2]或dp[i-1][j]
如果p的第j-1个字符与s的第i个字符不匹配，则处于无p得第j-1,j个字符状态，即dp[i][j-2]
情况2：如果第j个字符不是‘*’：如果s的第i个字符与p的第j个字符匹配或者p的第j个字符为‘.’，则当前状态与dp[i-1][j-1]一致,否则默认false

class Solution:
    def isMatch(self, s: str, p: str) -> bool:
        if not p:
            return not s
        m,n=len(s),len(p)
        dp=[[False] *(n+1) for i in range(m+1)]
        dp[0][0]=True
        for i in range(2,n+1):
            if p[i-1]=='*':
                dp[0][i]=dp[0][i-2]
        for i in range(1,m+1):
            for j in range(1,n+1):
                if p[j-1]=='*':
                    if s[i-1]==p[j-2] or p[j-2]=='.':
                        dp[i][j]=dp[i-1][j] or dp[i][j-2] 
                    else:
                        dp[i][j]=dp[i][j-2]
                elif s[i-1]==p[j-1] or p[j-1]=='.':
                    dp[i][j]=dp[i-1][j-1]
        return dp[-1][-1]

14. 最长公共前缀

初始化一个结果字符串，每次与新的字符串遍历，到第几个字符不一致则跳出，如果中途就变成空字符串，则说明不存在公共前缀

class Solution:
    def longestCommonPrefix(self, strs: List[str]) -> str:
        if len(strs)==0:
            return ''
        ans=strs[0]
        for i in range(1,len(strs)):
            j=0
            while j<len(ans) and j<len(strs[i]):
                if ans[j]!=strs[i][j]:
                    break
                j+=1
            ans=ans[:j]
            if ans=='':
                return ''
        return ans

28. 实现 strStr()

类似于滑动窗口

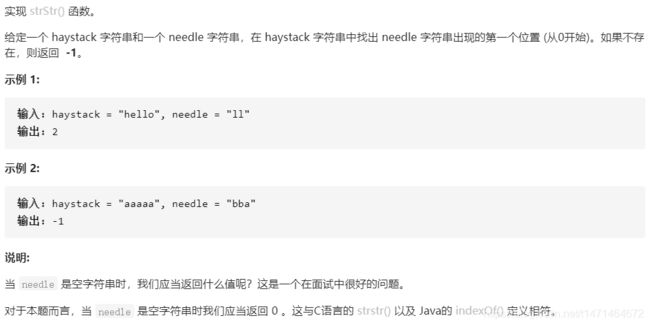
class Solution:
    def strStr(self, haystack: str, needle: str) -> int:
        if needle=='':
            return 0
        l=len(needle)
        for i in range(len(haystack)):
            if haystack[i:i+l]==needle:
                return i
        return -1

剑指 Offer 11. 旋转数组的最小数字

class Solution:
    def minArray(self, numbers: List[int]) -> int:
        left,right=0,len(numbers)-1
        while left<right:
            mid=left+(right-left)//2
            if numbers[mid]<numbers[right]:
                right=mid
            elif numbers[mid]>numbers[right]:
                left=mid+1
            else:
                right-=1
        return numbers[left]

36. 有效的数独

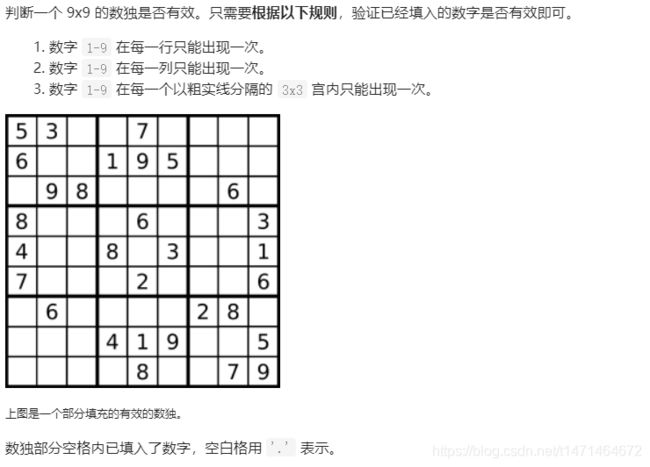
class Solution:
    def isValidSudoku(self, board: List[List[str]]) -> bool:
        row=[defaultdict(int) for i in range(9)]
        col=[defaultdict(int) for i in range(9)]
        box=[defaultdict(int) for i in range(9)]
        for i in range(9):
            for j in range(9):
                num=board[i][j]
                if num!='.':
                    num=int(num)
                    row[i][num]+=1
                    col[j][num]+=1
                    n=(i//3)*3+j//3
                    box[n][num]+=1
                    if row[i][num]>1 or col[j][num]>1 or box[n][num]>1:
                        return False
        return True

48. 旋转图像


法一：先转置，在逆转

class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        n=len(matrix[0])
        for i in range(n):
            for j in range(i,n):
                matrix[i][j],matrix[j][i]=matrix[j][i],matrix[i][j]
        for i in range(n):
            matrix[i].reverse()

法二：https://leetcode-cn.com/problems/rotate-image/solution/li-kou-48xiao-bai-du-neng-kan-dong-de-fang-fa-zhu-/
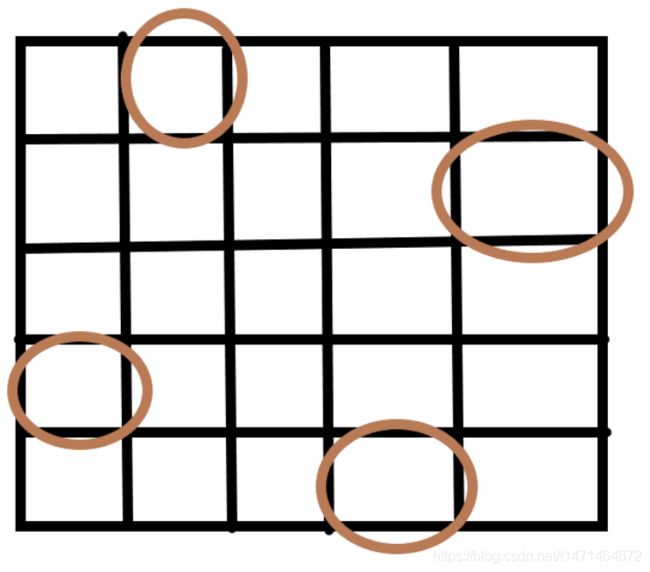
四个矩阵值为一组进行旋转，偏移量为add
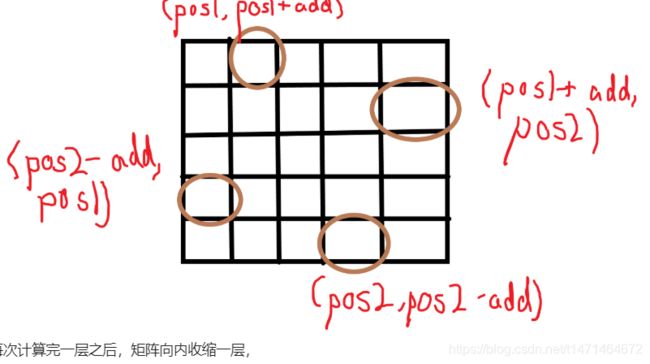
左上角的坐标为(pos1,pos1),右上角的坐标为(pos1,pos2),左下角的坐标为(pos2,pos1),右下角的坐标为(pos2,pos2),则能够写出偏移之后对应的坐标

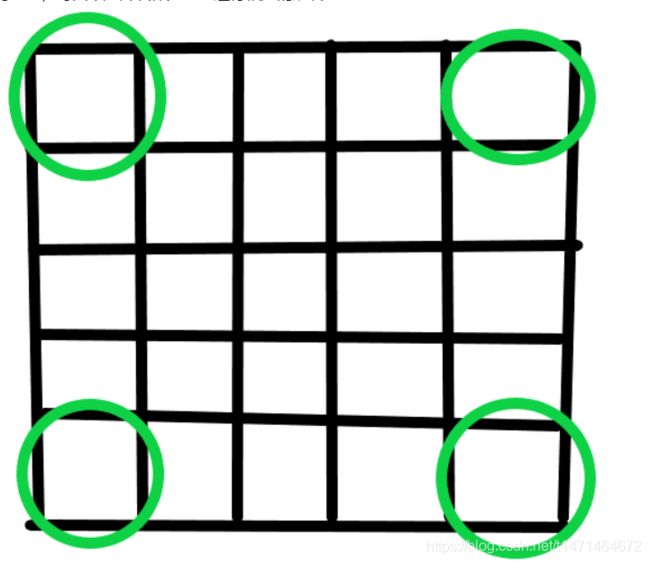
class Solution:
    def rotate(self, matrix: List[List[int]]) -> None:
        """
        Do not return anything, modify matrix in-place instead.
        """
        n=len(matrix[0])
        # for i in range(n):
        #     for j in range(i,n):
        #         matrix[i][j],matrix[j][i]=matrix[j][i],matrix[i][j]
        # for i in range(n):
        #     matrix[i].reverse()
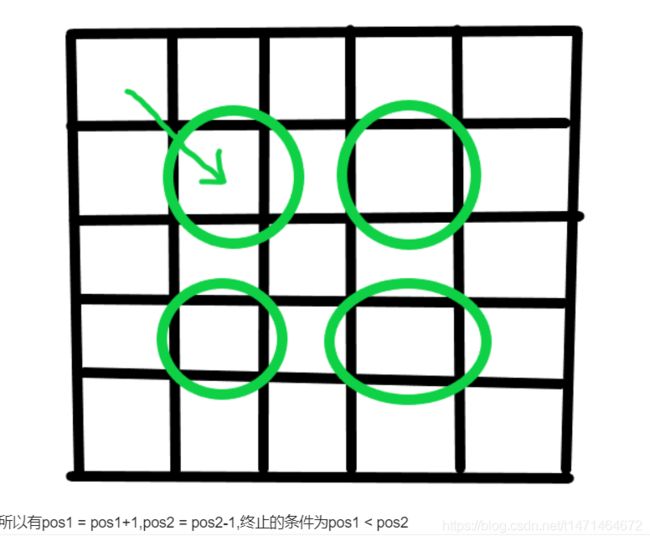
        pos1,pos2=0,n-1
        while pos1<pos2:
            add=0
            while add<pos2-pos1:
                tmp=matrix[pos2-add][pos1]
                matrix[pos2-add][pos1]=matrix[pos2][pos2-add]
                matrix[pos2][pos2-add]=matrix[pos1+add][pos2]
                matrix[pos1+add][pos2]=matrix[pos1][pos1+add]
                matrix[pos1][pos1+add]=tmp
                add+=1
            pos1+=1
            pos2-=1